
【Python】SimplePrograms 18 lines: 8-Queens Problem (recursion)
プログラム
18行プログラムです。
BOARD_SIZE = 8
def under_attack(col, queens):
left = right = col
for r, c in reversed(queens):
left, right = left - 1, right + 1
if c in (left, col, right):
return True
return False
def solve(n):
if n == 0:
return [[]]
smaller_solutions = solve(n - 1)
return [solution+[(n,i+1)]
for i in range(BOARD_SIZE)
for solution in smaller_solutions
if not under_attack(i+1, solution)]
for answer in solve(BOARD_SIZE):
print (answer)実行結果
[(1, 4), (2, 2), (3, 7), (4, 3), (5, 6), (6, 8), (7, 5), (8, 1)]
[(1, 5), (2, 2), (3, 4), (4, 7), (5, 3), (6, 8), (7, 6), (8, 1)]
[(1, 3), (2, 5), (3, 2), (4, 8), (5, 6), (6, 4), (7, 7), (8, 1)]
[(1, 3), (2, 6), (3, 4), (4, 2), (5, 8), (6, 5), (7, 7), (8, 1)]
[(1, 5), (2, 7), (3, 1), (4, 3), (5, 8), (6, 6), (7, 4), (8, 2)]
[(1, 4), (2, 6), (3, 8), (4, 3), (5, 1), (6, 7), (7, 5), (8, 2)]
[(1, 3), (2, 6), (3, 8), (4, 1), (5, 4), (6, 7), (7, 5), (8, 2)]
[(1, 5), (2, 3), (3, 8), (4, 4), (5, 7), (6, 1), (7, 6), (8, 2)]
[(1, 5), (2, 7), (3, 4), (4, 1), (5, 3), (6, 8), (7, 6), (8, 2)]
[(1, 4), (2, 1), (3, 5), (4, 8), (5, 6), (6, 3), (7, 7), (8, 2)]
[(1, 3), (2, 6), (3, 4), (4, 1), (5, 8), (6, 5), (7, 7), (8, 2)]
[(1, 4), (2, 7), (3, 5), (4, 3), (5, 1), (6, 6), (7, 8), (8, 2)]
[(1, 6), (2, 4), (3, 2), (4, 8), (5, 5), (6, 7), (7, 1), (8, 3)]
[(1, 6), (2, 4), (3, 7), (4, 1), (5, 8), (6, 2), (7, 5), (8, 3)]
[(1, 1), (2, 7), (3, 4), (4, 6), (5, 8), (6, 2), (7, 5), (8, 3)]
[(1, 6), (2, 8), (3, 2), (4, 4), (5, 1), (6, 7), (7, 5), (8, 3)]
[(1, 6), (2, 2), (3, 7), (4, 1), (5, 4), (6, 8), (7, 5), (8, 3)]
[(1, 4), (2, 7), (3, 1), (4, 8), (5, 5), (6, 2), (7, 6), (8, 3)]
[(1, 5), (2, 8), (3, 4), (4, 1), (5, 7), (6, 2), (7, 6), (8, 3)]
[(1, 4), (2, 8), (3, 1), (4, 5), (5, 7), (6, 2), (7, 6), (8, 3)]
[(1, 2), (2, 7), (3, 5), (4, 8), (5, 1), (6, 4), (7, 6), (8, 3)]
[(1, 1), (2, 7), (3, 5), (4, 8), (5, 2), (6, 4), (7, 6), (8, 3)]
[(1, 2), (2, 5), (3, 7), (4, 4), (5, 1), (6, 8), (7, 6), (8, 3)]
[(1, 4), (2, 2), (3, 7), (4, 5), (5, 1), (6, 8), (7, 6), (8, 3)]
[(1, 5), (2, 7), (3, 1), (4, 4), (5, 2), (6, 8), (7, 6), (8, 3)]
[(1, 6), (2, 4), (3, 1), (4, 5), (5, 8), (6, 2), (7, 7), (8, 3)]
[(1, 5), (2, 1), (3, 4), (4, 6), (5, 8), (6, 2), (7, 7), (8, 3)]
[(1, 5), (2, 2), (3, 6), (4, 1), (5, 7), (6, 4), (7, 8), (8, 3)]
[(1, 6), (2, 3), (3, 7), (4, 2), (5, 8), (6, 5), (7, 1), (8, 4)]
[(1, 2), (2, 7), (3, 3), (4, 6), (5, 8), (6, 5), (7, 1), (8, 4)]
[(1, 7), (2, 3), (3, 1), (4, 6), (5, 8), (6, 5), (7, 2), (8, 4)]
[(1, 5), (2, 1), (3, 8), (4, 6), (5, 3), (6, 7), (7, 2), (8, 4)]
[(1, 1), (2, 5), (3, 8), (4, 6), (5, 3), (6, 7), (7, 2), (8, 4)]
[(1, 3), (2, 6), (3, 8), (4, 1), (5, 5), (6, 7), (7, 2), (8, 4)]
[(1, 6), (2, 3), (3, 1), (4, 7), (5, 5), (6, 8), (7, 2), (8, 4)]
[(1, 7), (2, 5), (3, 3), (4, 1), (5, 6), (6, 8), (7, 2), (8, 4)]
[(1, 7), (2, 3), (3, 8), (4, 2), (5, 5), (6, 1), (7, 6), (8, 4)]
[(1, 5), (2, 3), (3, 1), (4, 7), (5, 2), (6, 8), (7, 6), (8, 4)]
[(1, 2), (2, 5), (3, 7), (4, 1), (5, 3), (6, 8), (7, 6), (8, 4)]
[(1, 3), (2, 6), (3, 2), (4, 5), (5, 8), (6, 1), (7, 7), (8, 4)]
[(1, 6), (2, 1), (3, 5), (4, 2), (5, 8), (6, 3), (7, 7), (8, 4)]
[(1, 8), (2, 3), (3, 1), (4, 6), (5, 2), (6, 5), (7, 7), (8, 4)]
[(1, 2), (2, 8), (3, 6), (4, 1), (5, 3), (6, 5), (7, 7), (8, 4)]
[(1, 5), (2, 7), (3, 2), (4, 6), (5, 3), (6, 1), (7, 8), (8, 4)]
[(1, 3), (2, 6), (3, 2), (4, 7), (5, 5), (6, 1), (7, 8), (8, 4)]
[(1, 6), (2, 2), (3, 7), (4, 1), (5, 3), (6, 5), (7, 8), (8, 4)]
[(1, 3), (2, 7), (3, 2), (4, 8), (5, 6), (6, 4), (7, 1), (8, 5)]
[(1, 6), (2, 3), (3, 7), (4, 2), (5, 4), (6, 8), (7, 1), (8, 5)]
[(1, 4), (2, 2), (3, 7), (4, 3), (5, 6), (6, 8), (7, 1), (8, 5)]
[(1, 7), (2, 1), (3, 3), (4, 8), (5, 6), (6, 4), (7, 2), (8, 5)]
[(1, 1), (2, 6), (3, 8), (4, 3), (5, 7), (6, 4), (7, 2), (8, 5)]
[(1, 3), (2, 8), (3, 4), (4, 7), (5, 1), (6, 6), (7, 2), (8, 5)]
[(1, 6), (2, 3), (3, 7), (4, 4), (5, 1), (6, 8), (7, 2), (8, 5)]
[(1, 7), (2, 4), (3, 2), (4, 8), (5, 6), (6, 1), (7, 3), (8, 5)]
[(1, 4), (2, 6), (3, 8), (4, 2), (5, 7), (6, 1), (7, 3), (8, 5)]
[(1, 2), (2, 6), (3, 1), (4, 7), (5, 4), (6, 8), (7, 3), (8, 5)]
[(1, 2), (2, 4), (3, 6), (4, 8), (5, 3), (6, 1), (7, 7), (8, 5)]
[(1, 3), (2, 6), (3, 8), (4, 2), (5, 4), (6, 1), (7, 7), (8, 5)]
[(1, 6), (2, 3), (3, 1), (4, 8), (5, 4), (6, 2), (7, 7), (8, 5)]
[(1, 8), (2, 4), (3, 1), (4, 3), (5, 6), (6, 2), (7, 7), (8, 5)]
[(1, 4), (2, 8), (3, 1), (4, 3), (5, 6), (6, 2), (7, 7), (8, 5)]
[(1, 2), (2, 6), (3, 8), (4, 3), (5, 1), (6, 4), (7, 7), (8, 5)]
[(1, 7), (2, 2), (3, 6), (4, 3), (5, 1), (6, 4), (7, 8), (8, 5)]
[(1, 3), (2, 6), (3, 2), (4, 7), (5, 1), (6, 4), (7, 8), (8, 5)]
[(1, 4), (2, 7), (3, 3), (4, 8), (5, 2), (6, 5), (7, 1), (8, 6)]
[(1, 4), (2, 8), (3, 5), (4, 3), (5, 1), (6, 7), (7, 2), (8, 6)]
[(1, 3), (2, 5), (3, 8), (4, 4), (5, 1), (6, 7), (7, 2), (8, 6)]
[(1, 4), (2, 2), (3, 8), (4, 5), (5, 7), (6, 1), (7, 3), (8, 6)]
[(1, 5), (2, 7), (3, 2), (4, 4), (5, 8), (6, 1), (7, 3), (8, 6)]
[(1, 7), (2, 4), (3, 2), (4, 5), (5, 8), (6, 1), (7, 3), (8, 6)]
[(1, 8), (2, 2), (3, 4), (4, 1), (5, 7), (6, 5), (7, 3), (8, 6)]
[(1, 7), (2, 2), (3, 4), (4, 1), (5, 8), (6, 5), (7, 3), (8, 6)]
[(1, 5), (2, 1), (3, 8), (4, 4), (5, 2), (6, 7), (7, 3), (8, 6)]
[(1, 4), (2, 1), (3, 5), (4, 8), (5, 2), (6, 7), (7, 3), (8, 6)]
[(1, 5), (2, 2), (3, 8), (4, 1), (5, 4), (6, 7), (7, 3), (8, 6)]
[(1, 3), (2, 7), (3, 2), (4, 8), (5, 5), (6, 1), (7, 4), (8, 6)]
[(1, 3), (2, 1), (3, 7), (4, 5), (5, 8), (6, 2), (7, 4), (8, 6)]
[(1, 8), (2, 2), (3, 5), (4, 3), (5, 1), (6, 7), (7, 4), (8, 6)]
[(1, 3), (2, 5), (3, 2), (4, 8), (5, 1), (6, 7), (7, 4), (8, 6)]
[(1, 3), (2, 5), (3, 7), (4, 1), (5, 4), (6, 2), (7, 8), (8, 6)]
[(1, 5), (2, 2), (3, 4), (4, 6), (5, 8), (6, 3), (7, 1), (8, 7)]
[(1, 6), (2, 3), (3, 5), (4, 8), (5, 1), (6, 4), (7, 2), (8, 7)]
[(1, 5), (2, 8), (3, 4), (4, 1), (5, 3), (6, 6), (7, 2), (8, 7)]
[(1, 4), (2, 2), (3, 5), (4, 8), (5, 6), (6, 1), (7, 3), (8, 7)]
[(1, 4), (2, 6), (3, 1), (4, 5), (5, 2), (6, 8), (7, 3), (8, 7)]
[(1, 6), (2, 3), (3, 1), (4, 8), (5, 5), (6, 2), (7, 4), (8, 7)]
[(1, 5), (2, 3), (3, 1), (4, 6), (5, 8), (6, 2), (7, 4), (8, 7)]
[(1, 4), (2, 2), (3, 8), (4, 6), (5, 1), (6, 3), (7, 5), (8, 7)]
[(1, 6), (2, 3), (3, 5), (4, 7), (5, 1), (6, 4), (7, 2), (8, 8)]
[(1, 6), (2, 4), (3, 7), (4, 1), (5, 3), (6, 5), (7, 2), (8, 8)]
[(1, 4), (2, 7), (3, 5), (4, 2), (5, 6), (6, 1), (7, 3), (8, 8)]
[(1, 5), (2, 7), (3, 2), (4, 6), (5, 3), (6, 1), (7, 4), (8, 8)]解説
「8-Queens Problem」って、なに?
「8-Queens Problem」というのは、チェス盤とクイーンの駒を使ったパズルです。
ルールは簡単。
『チェスの盤上に、8個のクイーンを配置する。このとき、どの駒も他の駒に取られるような位置においてはいけない。』
チェスのクイーンというのは、四方八方に制限なく動くことができます。
解はもうわかっています。
ですが、プログラムで答えを探すのには最適かもしれません。総当たりでチェックするのは、プログラムにとって得意中の得意ですから。
プログラムについて
タイトルにある「recursion」の意味は「再帰呼出」です。
面食らいました。
チュートリアルで、再帰呼出とは!
コードを見て更に驚愕。
なんじゃこりゃあ!
と思いませんか?
関数「solve」の戻り値。
4行1文のリスト内包表記です。
再帰呼出とリスト内包表記。
うーむ。
プログラム解説
どう解説すればええのか。
動きを絵にすればどうかと思ったけど、あっという間に爆発的に膨らんでしまう。
とにかく、えっちらおっちらやってみます。
まず、関数「solve」を引数「8」で呼び出します。
「solve」の入り口は、引数が「0」でなければ引数を1つ引いて自分自身を呼び出します。
こんな感じ。
solve(8)
→solve(7)
→solve(6)
→solve(5)
→solve(4)
→solve(3)
→solve(2)
→solve(1)
→solve(0)solve(0)
「0」にあたったら、リスト [[]] を返します。
→solve(0)
return [[]]solve(1)
「solve(1)」は空のリストを受け取ってどうするでしょう。
こんなことをします。

「smaller_solutions」が 「solve(0)」から得た空のリスト。
最初は空ですので次の値で1回まわるだけです。
solution = []これで4行のうちのループを1つ解決しました。
残り3行。
最後の行の if 文を脇へ置きましょう。
するとこうなります。
[solution+[(n,i+1)]
for i in range(BOARD_SIZE)]これは次のようなループになります。
solution = []
n = 1
i = 0 ~ 7
ですから、こんな結果になります。
[
[(1, 1)],
[(1, 2)],
[(1, 3)],
[(1, 4)],
[(1, 5)],
[(1, 6)],
[(1, 7)],
[(1, 8)]
]そしてこれに次のような条件が加わります。
if not under_attack(i+1, solution)]「under_attack」は、「他のクイーンの攻撃位置にあるとき」に True で返ります。それに「not」がついているわけですから、「他のクイーンの攻撃位置でないとき」にこの条件が成立するわけです。
関数「under_attack」ですが、今回の場合第2引数が [] と空のリストですので、for 文は一度もループしません。ですから、 False が返ることになります。「まだどこにも他のクイーンがいないので攻撃されることはない」ということですね。
ですので、先ほどのリストがそのまま返ります。
リスト1
[
[(1, 1)],
[(1, 2)],
[(1, 3)],
[(1, 4)],
[(1, 5)],
[(1, 6)],
[(1, 7)],
[(1, 8)]
]ここまでは難しくない。
これから徐々にややこしくなります。
solve(2)
「solve(2)」はリスト1を受け取ってループします。
for solution in smaller_solutionsループ1回目 solution = [(1, 1)]
ループ2回目 solution = [(1, 2)]
ループ3回目 solution = [(1, 3)]
ループ4回目 solution = [(1, 4)]
ループ5回目 solution = [(1, 5)]
ループ6回目 solution = [(1, 6)]
ループ7回目 solution = [(1, 7)]
ループ8回目 solution = [(1, 8)]
まずは、1回目のループを考えましょう。
やはり if 文を脇へ置きます。
するとこうなります。
[solution+[(n,i+1)]
for i in range(BOARD_SIZE)]今回は次のようなループになります。
solution = [(1, 1)]
n = 2
i = 0 ~ 7
無条件に処理すると次のようになります。
[
[(1, 1), (2, 1)],
[(1, 1), (2, 2)],
[(1, 1), (2, 3)],
[(1, 1), (2, 4)],
[(1, 1), (2, 5)],
[(1, 1), (2, 6)],
[(1, 1), (2, 7)],
[(1, 1), (2, 8)]
](1, 1) のマスに
2行目のマス (2, 1) ~ (2, 8) を
それぞれつなげた感じですね。
でもこれだと (1, 1) と (2, 1) は互いに攻撃対象になってしまいます。これは条件に反してしまう。その条件を判定するのが関数「under_attack」です。
関数「under_attack」については後述します。
少なくとも、マス (1, 1) にクイーンを置いた場合、図のグレーの部分に他のクイーンは置けません。

関数「under_attack」の結果が True となってリストから省かれます。従って、 solution = [(1, 1)] のループの結果は次のようになります。
[
[(1, 1), (2, 3)],
[(1, 1), (2, 4)],
[(1, 1), (2, 5)],
[(1, 1), (2, 6)],
[(1, 1), (2, 7)],
[(1, 1), (2, 8)]
]solution の他のケースについても同様にリストが作られます。
solve(4)
少し先に進めて solve(4) で次のケースを考えてみましょう。
solution = [(1, 1), (2, 5), (3, 8)]
n = 4
i = 0 ~ 7
既に3つのクイーンが配置されています。
このため下図のグレー部分にはクイーンを配置できません。4行目は2番目、6番目の列にしか置けない。
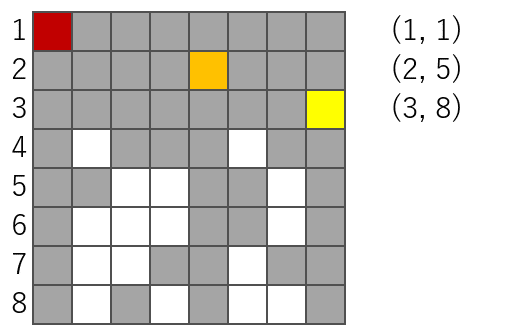
ですから結果はこうなる。
[
[(1, 1), (2, 5), (3, 8), (4, 2)],
[(1, 1), (2, 5), (3, 8), (4, 6)],
]以上を solve(8) まで繰り返すことで解を得ます。
under_attack
だんだん長くなってきたので次の記事に回します。
詳しくはこちらで。
問題
ふと思いませんか?
関数「under_attack」は再帰呼出で書けないのかって。
関数「solve」は再帰呼出を使わないで書けないのかった。
ここで問題です。
(1)関数「under_attack」を再帰呼出で書けるでしょうか。
(2)関数「solve」を再帰呼出を使わずに書けるでしょうか。
再帰呼出の練習にはちょうどいいかもしれません。
回答
上記問題の回答はこちらに。
リスト内包表記いろいろ
いろいろなリスト内包表記についてはこちら。
理屈はわかったけど書き方を忘れた時に便利。
