関数「under_attack」解説

先の記事『8-Queens Problem』における関数「under_attack」について解説を追記します。

記事『8-Queens Problem』についてはこちら。

---

関数「under_attack」

まず、関数「under_attack」を再掲します。

def under_attack(col, queens):
    left = right = col

    for r, c in reversed(queens):
        left, right = left - 1, right + 1

        if c in (left, col, right):
            return True
    return False

---

solve(4)

前記事に記載した solve(4) で使用したパターンを考えます。

既に、
solution = [(1, 1), (2, 5), (3, 8)]
にクイーンを配置しています。

---

(4, 7)

まず、 (4, 7) に置くことができるかどうか考えてみます。
下図の★印のマスです。

このとき、関数「under_attack」は次のように呼び出されます。

under_attack(7, [(1, 1), (2, 5), (3, 8)])

初めに、

left = right = col = 7

でスタートします。

ループは

for r, c in reversed(queens):

ですから、「queens」を逆順に処理します。

「queens」は、

queens = [(1, 1), (2, 5), (3, 8)]

です。
「reversed」がなければ

(1, 1)→(2, 5)→(3, 8)

の左から右の順序で処理されますが、
「reversed」があると

(1, 1)←(2, 5)←(3, 8)

右から左の順序で処理されます。

left, right = left - 1, right + 1

で、

• left を1つ左に

• right を1つ右に

ずらします。

すなわち、下図の「Ｌ」「Ｃ」「Ｒ」が、それぞれ、left、col、rightに対応し、この3つのマスにクイーンがあるかどうかをチェックするわけです。

このケースの場合、「Ｒ」のマスにクイーンがいるため、次の条件にヒットします。

if c in (left, col, right):

この条件文は
「c が、 left か col か right のどれかと一致したら真」
という意味になります。

---

(4, 3)

では、(4, 3) にクイーンは配置できるでしょうか。
下図の★印のマスです。

まず、ループの最初の ＬＣＲ はここになります。
ＬＣＲ のどこにもクイーンはいません。

ですので、次のループに進みます。
このとき、left、right は更に左右に1つずつずれるので、次のようになります。

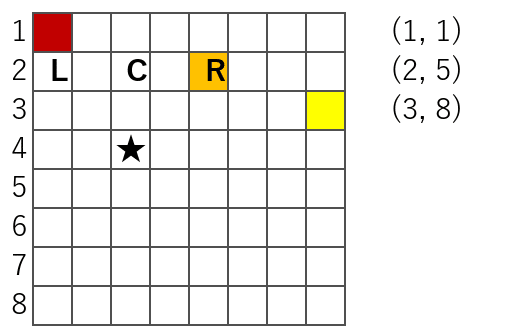
ここには「Ｒ」のマスにクイーンがいるため、★印のマスには置けません。

---

(4, 4)

では、(4, 4) は？

最初のループ。
ＬＣＲ のどこにもクイーンはいません。

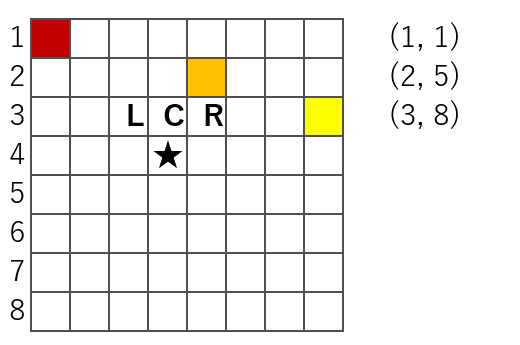
次のループ。
ここにもクイーンはいません。

そして最後のループ。
「Ｌ」のマスにクイーンがいます。
やはり★印のマスには置けません。

---

(4, 6)

ちなみに (4, 6) であれば、3回のループの ＬＣＲ のどこにもクイーンはいません。ですから (4, 6) には新たにクイーンを置けることになります。