
数学夏祭り 第五問解説(α-βゴリ押し解法)
こんにちは
今回は数学夏祭りの第五問を解説していきます。例によって強引な解法ですので、きれいな解法をご所望の方は回れ右してください。
今回、途中で「ファウルハーバーの公式」(一部分)なるものを使いますが、僕は知らなかったので証明を独自でしました。ネットは見てないので証明方法が定石ではないかもしれませんが、そこはご了承ください。逆に言えば、知らなくても解けるよ、ということですね。
さて、長い前置きはここまでで解法に入っていきます。
αを求める
まず、ゴリ押しと評されている通り、αを出します。問題文的にαを具体的に出してほしくない雰囲気を醸し出しているので、多分私の解法は邪道。
anを見ると、シグマとリミットが入ってますね。そこで理系の皆さんはピンと来てほしいです、、、そう区分求積法ですね。解いていきます。

理系の皆さんは余裕ですよね・・・?
これで、α=1/80だとわかりました。
Kの考察
今度はKを詳しく見てみましょう。下図を見てください。Σ[k=1…n]k^79はn^80が最高次だと仮定して記述していますが、あくまで仮定。あとでちゃんと証明しますよ。

nを∞に飛ばすにあたって、n^80の係数(上図内でβと置いたところ)は1/80であってほしいですね(上から2番目の式のところですよ)。Kが発散してしまいます(一番下の式を見てください。nの係数が残るとまずいですね)。あと、n^81以上があっても発散してしまいますね。これらを考慮すると示したいことは以下のことです。

ファウルハーバーもどきを導出する
数学的帰納法で証明します。

数学的帰納法の中でも異色の方法を使います。p≦lの場合をすべて成立すると仮定します。この方法、俗になんというかコメントで教えてください。ここで大事なのは、Σ[k=1…n]k^pの中には、n^(p+2)以上の項はない(n^(p+2)以上の項の係数は0)、ということです。さて、p=l+1の時が正しければいいですね。ここで神のお告げが来ます。

こんなの思いつかんわ、とお思いのあなた、この式は私の経験がもたらしたものです。数研出版の数学Bの教科書のp.91に似たような式があります。(教科書変わってたらすみません)。いわゆる、シグマの公式を導き出すときに使っている式です。教科書は意外と大事だと痛感します。
次にk=1からnまで具体的に入れてみます。
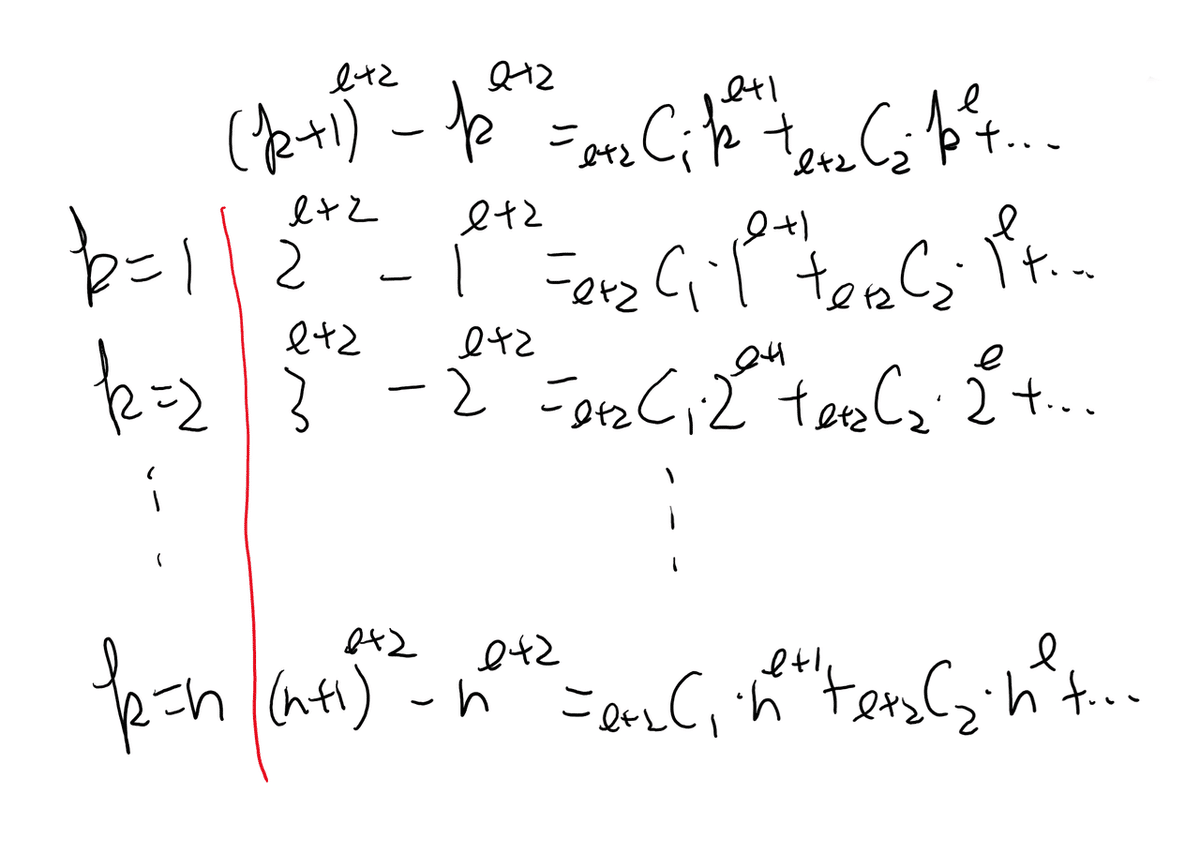
これを左辺は左辺、右辺は右辺で足し算します。

ここで大事なのは、p≦lの場合をすべて成立すると仮定したので、図の「…」のところにn^(l+1)の項はない、ということです。さて、求めたい式がありますね。

Σ[k=1…n]k^(l+1)について解くと、(一気に解いてしまいますよ)

Σ[k=1…n]k^l は計算してしまいましたよ。ここで、n^(l+2)に関係しているのは下図の赤いところだけです。そこを計算すると、

証明終了です。
あれ、まだ答え出せないよね?
もう一度この式を見てみましょう。

△がわからないと答えは出ません。(△はきついので、そろそろγに置き換えます)。でも実は、上の証明でn^(l+1)まで見てあげると値が出ています。
より詳しく
途中から見ますよ。

まず、赤のところを計算します。

n^(l+1)の係数は1ですね。次に青のところを計算します。

n^(l+1)の係数は-1/2ですね。これらを足し合わせると、n^(l+1)の係数は1/2ですね。ついでにγ=1/2がわかってしまいました。ちょっと論理がわかりにくいので図で整理します。

やっとこさKの値
上の証明からわかることは以下のことです。

これを使ってKの値を求めていきましょう。
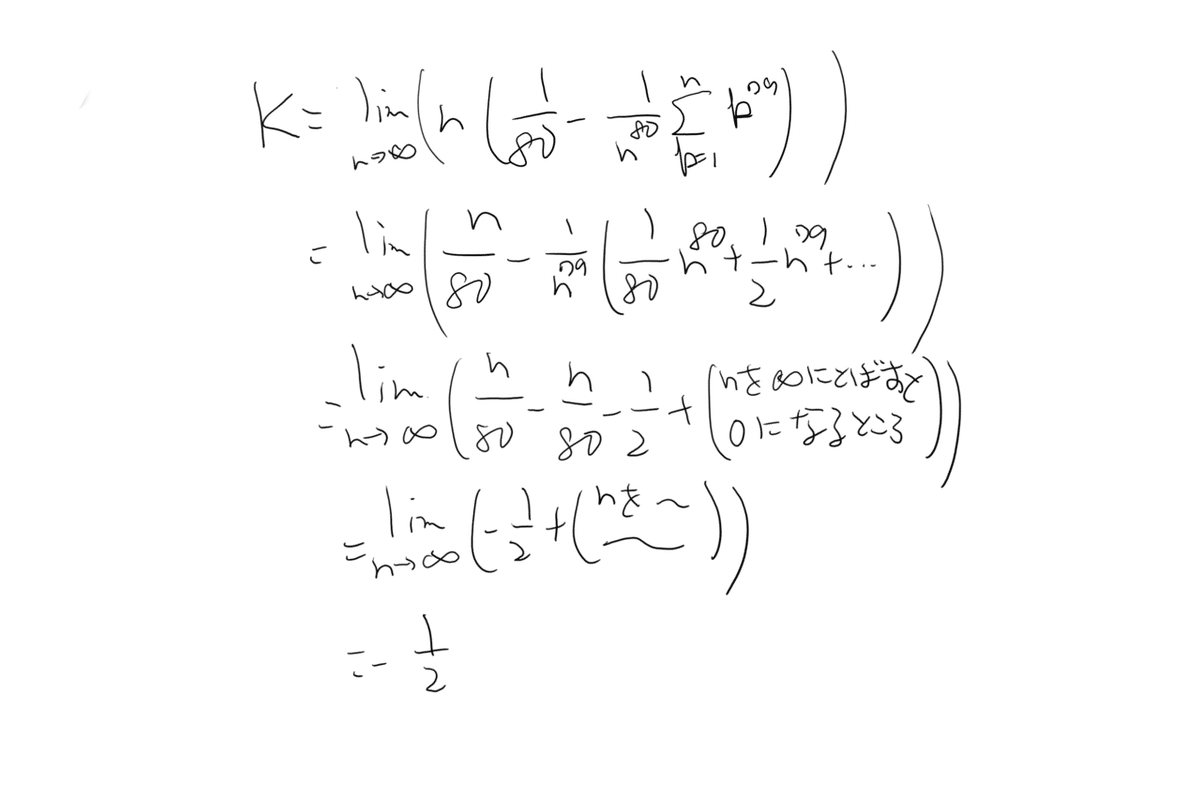

答えは100でした。ここまで見ていただきありがとうございます。わかりにくいところがあればコメントしてください。私が成長します。
