
数学夏祭り 問2解説(非推奨な解き方)
こんにちは。今回は数学夏祭りの問2を解説していきます。私の紹介する解き方はとても計算が面倒くさく、煩雑なため非推奨です。こんな解き方があるんだなぁ、くらいで見てくれたらうれしいです。
座標平面に三角形を置く
座標平面に三角形を置くとA、B、Cに座標を与えることができます。
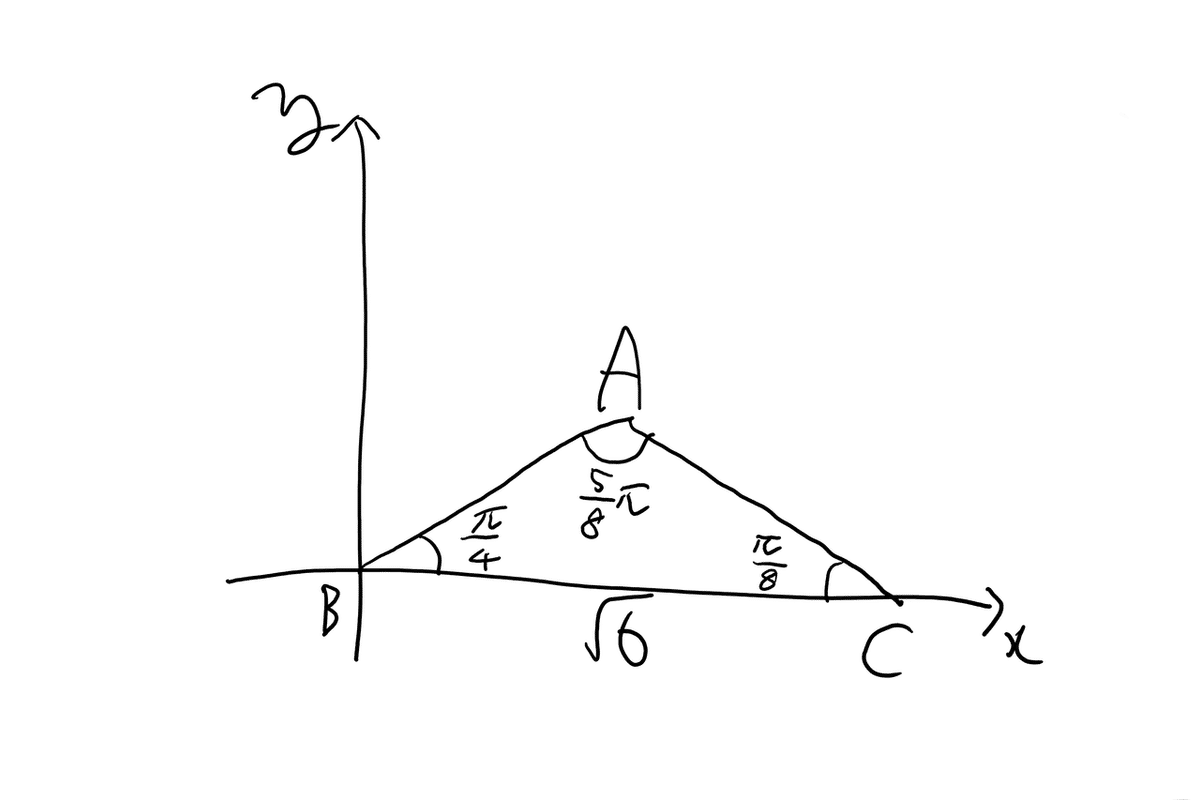
B(0,0) C(√6,0)ですね。Aの座標はわからないので求めてみましょう。
正弦定理で求めたいのですが、sin(π/8)とsin(3π/8)を求めなければいけませんね。(なんでsin(3π/8)を求めるの?と思った方、とりあえず読み進めてください。)
半角の公式より、

よって正弦定理より、(sin(5π/8)=sin(3π/8)を途中使った)


さて、これで下準備が終わりました。同様にH、O、G、L、Dの座標を求めていきましょう。
Hの座標を求める
HはAの真下にあることを考慮すると、H(√3(√2-1), h)と置ける。(hは実数)
BHとACは垂直に交わるので、(太字の文字はベクトルを表しています。画像内では文字の上に右矢印を乗せて表現しています)
BH・AC=0

よって、H(√3(√2-1), 3)
Oの座標を求める
まず、外接円の半径を求める。
外接円の半径をRと置くと、正弦定理より、

次にO(a,b)と置く。(a,bは実数)
OとBに注目した式は、

また、OとCに注目した式は、
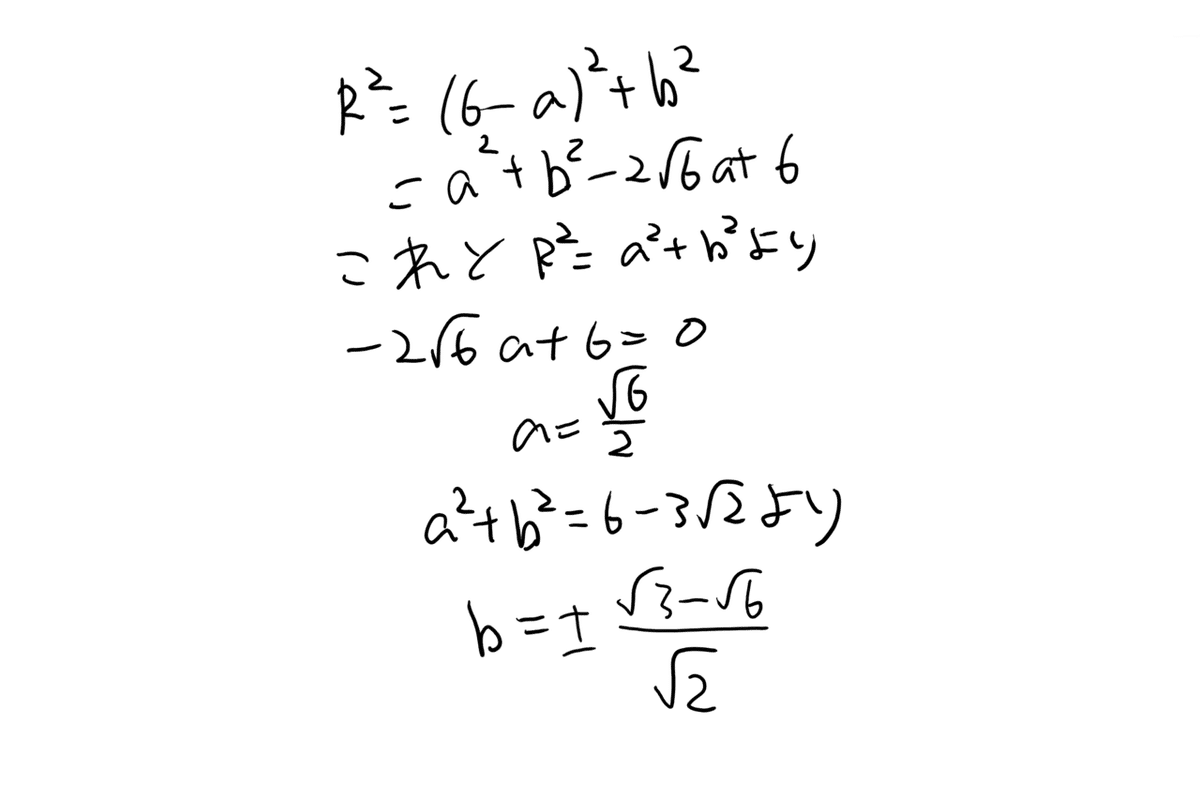

やっとOが求まりました。大変ですがまだ半分も解けていませんよ!
Gの座標を求める
BとCの中点をG'と置くと、

G'=(√6/2, 0) よって、

Lの座標を求める
L(c,d)と置く。

やっとDの座標を求める
なんとかここまで計算してきましたが、ここでmとnという文字が入り計算が面倒くさくなります。でも大丈夫です。計算は裏でやっておきますよ!
DはGLをm:nに外分するので、

はい、煩雑ですね。これ以降の計算が面倒くさいのが目に見えます。
四角形ABDCの面積を求める
まず、4点の座標がわかっているときの面積の公式を載せておきます。こんな解き方あるんですね・・・(調べて簡単でびっくり)

ブレートシュナイダーの公式を使っていたら、私の手は今頃・・・
さて、解いていきます。
今回はこの式に、

を当てはめたらいいですね。
これより、

y3+y4=y2+y3, y4+y1=y1+y2なので、


なので、

お疲れさまでした。ここまで見ていただきありがとうございます。
