逆関数と合成関数（数Ⅲ）

こんにちは。

今回は数Ⅲで習う逆関数と合成関数について扱います。分数関数や無理関数と違ってどんなものか想像しづらい名前ですが頑張っていきましょう。

逆関数の前に

逆関数というのを扱うには関数をもってこなければいけないのですが、関数とは何か知っていますか？軽く解説しておきます。(下の内容が難しかったら、逆関数とは、まで飛ばしてもいいです。)

まず変数xを用意します。(身構えなくていいですよ！いつも使っているxです。)　xを入れるとf(x)を返してくれるものを関数といいます。

y=f(x)で、この関係が成り立っているとき、yはxの関数、といいます。

逆関数を扱ううえで大事なのが、yはxの関数であり、xはyの関数でなければいけない、ということです。別の言い方をすると、xとf(x)は一対一対応でなければいけないということです。

具体例で理解を深めましょう。下のような関数を用意します。

左のグラフ(y=x+1)はxを一つ決めるとyが一つ決まるので、yはxの関数です。逆に、yを一つ決めるとxが一つ決まるので、xはyの関数とも言えます。

右のグラフ(y=x^2)はxを一つ決めるとyが一つ決まるので、yはxの関数です。でも、yを一つ決めるとxが2つも決まってしまいます。この時は、xはyの関数とは言えません。

今回扱う逆関数ではyはxの関数であり、xはyの関数であるもの（一対一対応の関数)にしか定義されません。つまり、y=x+1の逆関数は存在し、y=x^2の逆関数は存在しないです。(x≧0として無理やり逆関数を作ることもできます。)

逆関数とは

やっと逆関数について話していきます。

逆関数は簡単に言うと、xとyを入れ替えた関数です。少しやってみましょう。次の例題を見て感覚をつかんでください。

例

y=2x-4の逆関数を求める。

xとyを入れ替えて、

x=2y-4

yについて解いて、

y=(x/2)+2

どうですか。わかりましたか？上の例題において、y=2x-4の逆関数はy=(x/2)+2で、y=(x/2)+2の逆関数はy=2x-4です。

(補足事項：y=f(x)の逆関数をy=f-1(x)と書き、「エフインバース」と読む)

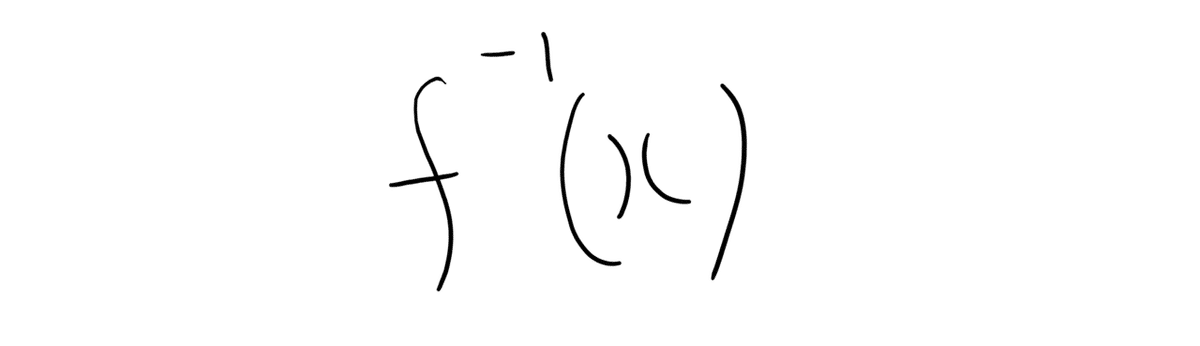
逆関数を考えて何が面白いの？

なんかxとyをひっくり返しただけで何が面白いの？と思うかもしれません。しかし逆関数の特徴はとても面白いものです。

まず、元の関数とその関数の逆関数は直線y=xに対して対象です。上の例の問題を使って自分で確かめてみてください。

この性質を使うとあることがわかります。

y=a^xの逆関数を考えてみましょう。(aは0より大きく1ではありません)

xとyを入れ替えて

x=a^y

両辺aを底とする対数をとって、([]の中身を底としています)

log[a]x=log[a]a^y

よって、

log[a]x=y

これよりy=a^xとy=log[a]xはy=xで対称であることがわかりました！！

逆関数の注意点

逆関数を扱う際に注意しなければいけないことがあります。それが定義域と値域です。

(ここでは定義域はxの範囲を、値域はyの範囲のことですよ。)

例えば、もとの関数の定義域が3<x<6となっていたとします。すると逆関数はxとyが入れ替わるので、逆関数の値域が3<y<6になります。逆に、元の関数の値域が0<y<2であると、逆関数の定義域が0<x<2になります。

合成関数

合成関数とは簡単に言うと、ある関数(f(x)とする)を別の関数(g(x)とする)のxに突っ込んで作られる関数のことです。つまり

g(f(x))

ということです。ちなみに、g(f(x))を

(g◦f)(x)

と書くこともあります。

具体例で理解を深めましょう。

f(x)=x+2   g(x)=x^2  とすると、

(g◦f)(x)=g(f(x))=g(x+2)=(x+2)^2

合成関数で注意することは

(g◦f)(x)と(f◦g)(x)は必ずしも一致しないことです。

上の例でみてみると、

(f◦g)(x)=x^2+2

となり、(g◦f)(x)と一致しません。

(あと、細かいところでは、f(x)の値域がg(x)の定義域に入っていなければいけない、というのがあります。この時でも、f(x)の定義域(値域)をいじれば合成関数を作れたりするのですが、ややこしいので頭の片隅にいれておくだけでいいです。)

合成関数を学んで何がしたかったのか、というのはいまのところ、とりあえずこういう考え方がある、ということを知ってほしかったのみです。今度合成関数が現れるのは微分のところです・・・お楽しみに！

今回はここまで、次回は極限に入っていきます。