2024年一級建築士学科試験合格者数予想、製図受験有資格者数について
はじめに
昨年「2023年一級建築士学科試験合格者数予想、既受験製図合格率について」という記事を書き、その中でR5年学科合格者数予想を5700名程度だろうとしました。実際には学科合格者数は4562名でおよそ1100名の差があり、記事の内容に大きな誤りがあることがわかりました。
本記事では「2023年一級建築士学科試験合格者数予想、既受験製図合格率について」において誤りであった内容の確認、およびR5の結果も踏まえて改めてR6年の学科合格者数や学科免除者(製図受験有資格者)数を予想し、試験の動向を探りたいと思います。
昨年の誤謬の原因
事実として把握できる数字
そもそも、ですが「2023年一級建築士学科試験合格者数予想、既受験製図合格率について」についてはデータ上の数字を文字のみで記載しており読んでくださった方にはその整合性や妥当性が非常にわかりにくいものになっていました。もちろん私は手元のメモに詳細な数字を記入して記事にしていましたが資格学校等公表の数字や表を参照しても比較しにくくストレスを与える内容であったことは反省しています。
今年は記載している内容の根拠等も確認いただけるよう表も併記して筆を進めたいと思います。
昨年の予想の軸は「カド番受験生の合格率は10%程度」でした。この割合はR1年においては結果から得られる事実ですが、まずはその確認をしたいと思います。
下記表①は試験元公表の数字及びそれを元に算出出来る数字のみ記入しています。年号は受験要件緩和以前以後での色分け、表内グレーは緩和以前の試験です。
緩和以前は「i列:製図からの製図受験者数」と「s列:製図受験有資格者数」は同じとなっていますが、実際には受験資格を持ちながらも受験しなかった方や止むを得ない事情により受験出来なかったもおられるはずなので「s列人数>i列人数」だと思います。ただそのような未受験者数は知る由もないため、また少数であると思われるためここでは無視して考えます。
「q列」は製図受験可能回数ごとの人数です。③なら3回受験可能、つまり前年学科合格の保留者を現します。❸も3回受験可能ですが2回続けて保留している人数、❷は1度落ちた前年製図保留者数を意味します。R2年以前は❷と②がありますが製図保留の制度がなかった為❷は前年受験しなかった人数(受験しなくても受験可能回数は減る)、②は前年不合格であった人数となります(※訂正:R5、R6の「q列」3段目、「❸/❷ 」→「 ❸/❷/❶」です)。
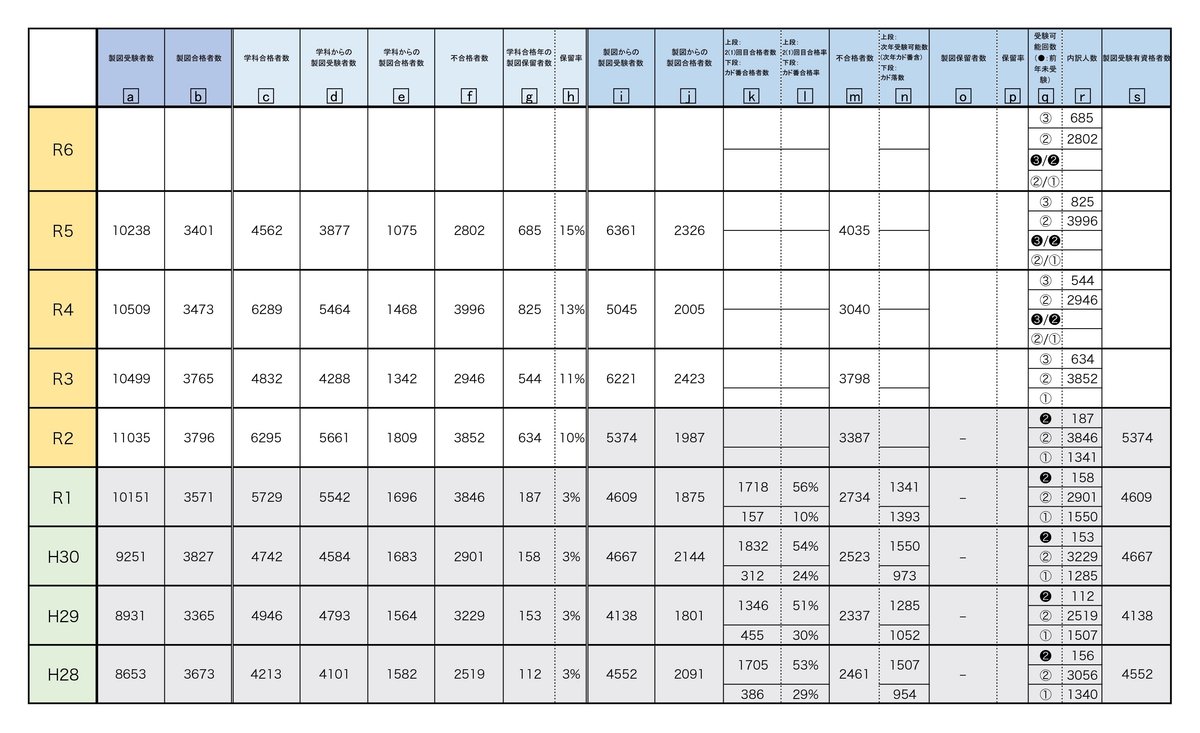
「g列:学科合格年の製図保留者数」は試験元公表の資料より正確にわかります(「c列:学科合格者数」ー「d列:学科からの製図受験者数」)。
また「f列:学科からの製図不合格者数」も正確にわかります(「d列:学科からの製図受験者数」ー「e列:学科からの製図合格者数」)。
これらの数字から緩和以前は「カド番受験者数」がかなり正確にわかりました(「s列」ー前年「g列」ー前年「f列」)。かなり、なのは上記でふれた「s列」の無視している人数分(製図受験していない人数分)だけカド番受験生が多い可能性があるためです。
緩和以前は「カド番受験者」=「m列:前年の製図からの製図不合格者数」ー「前年のカド落受験者数」となるため逆算して「前年のカド落受験者数」もわかりました。「カド落受験者数」が分かれば「カド番受験者数」ー「カド落受験者数」=「カド番合格者数」がわかります。ここから「カド番の合格率」および「カド番以外の製図からの製図合格率」も割り出すことが出来ました(「k列」、「l列」)。
「2023年一級建築士学科試験合格者数予想、既受験製図合格率について」でも書いた通り、「カド番以外の製図からの製図合格率」は50%〜55%で変化がない中、R1年は「カド番の合格率」が10%と大きく下落しており試験元の合否判定に対する何らかの意図的な変更があったのではないか、と考えました。
ただ表①からも分かる通り、R3年製図試験よりR2年の受験要件緩和(試験においては2回まで製図スキップ可能)の受験生がいるため正確な「s列」の数字がわからない状況になりました。つまりR3年から「カド番受験者数」を根拠を持って示すことが出来なくなりました。「2023年一級建築士学科試験合格者数予想、既受験製図合格率について」では仮に「カド番受験生の合格率は10%程度」を前提とした場合、もろもろの数字に矛盾が生じないことを根拠に「カド番受験生の合格率は10%程度」であると考え、さらにそこからR5年の学科合格者数を予想するということをしました。結果大きな齟齬があったわけですがその原因は「カド番受験生の合格率は10%程度」という前提そのものというより予想の中で採用した他の前提の数値「試験元の製図受験者数想定上限値:11000人」と「製図試験保留率:7%」が誤っていたためと考えられます。
以下、それらが誤っていた、と考える根拠を書きます。
試験元は製図受験者の上限値を想定している?
まず「試験元の製図受験者数想定上限値:11000人」ですが、これは試験元が受験人数を最もコントロール出来たであろうR2年の製図試験受験者数(「a列」)が11035人であったことを根拠にしていました。「試験元が製図受験者の上限値を想定している」という事実は当然公表されていませんしそれ自体が私の予測です。
回りくどいですがこの記事において大事なのでこの考えの根拠についてまず書きたいと思います。
そもそも受験資格要件の緩和は少子化等による受験者数の減少と同時に高齢化により有資格者の減少の流れの中で有資格者数の維持が目的の一つであることに疑問はないかと思います。
その中で単に従来の受験資格を満たしていない若い受験者を増やすだけでは資格としての一定のレベル維持が難しいということで実務要件緩和の代わりに免許取得要件が設けられていますが、個人的には本質的な意味で実務要件の緩和で試験を受けやすくなった代わりに設けられたものは「製図は5年中3回受験可能」という「緩和」だと思っています。緩和の代わりに「緩和」、というのはおかしいのですが、要は「製図は5年中3回受験可能」は「緩和」ではなく実は「要件強化」だと考えられます。
「製図は5年中3回受験可能」となることで製図受験の保留が可能となり準備に時間をかけたりすることで戦略的に製図試験に臨むことが可能になります。この点においては緩和であることは間違いありません。ただこのことは同時に潜在的な製図受験有資格者数が増えることを意味します。
こうして製図受験者数が増えるという状況になれば合格者数を維持しながら総合合格率を抑えることが可能になり、それはイコール製図試験の合格難易度が上がることを意味します。これは同時に準備が万全となりにくい学科合格からの製図ストレート合格者が少なくなることを意味し、1年で試験を終えるのは優秀な一部の人たちに限られることになります。
つまり最初の学科試験は緩和によって受けやすくなる代わりに実質的な合格難易度は上がっていることになり要件が強化されていると言えます。
仮に「製図は5年中3回受験可能」という条件がなければ総合合格者数維持=製図試験受験者数維持のため一定以上の学科合格者数とその中からの製図ストレート合格者数を確保し続けなければなりません。
これは総合合格者レベルの維持だけでなく総合合格率(再び受験者が減ればいずれ上昇)を抑えることも難しいことを意味しますが潜在的な製図受験有資格者がいることで総合合格者レベルの維持や総合合格率の抑制だけでなく、製図試験受験者数に上限を設けることで学科の合格者数を抑えることも可能(=学科合格者のレベル維持が可能)になります。
長くなりましたがこれが私が「試験元が製図受験者の上限値を想定している」と考える理由です。
R1年に学科の合格率が高くなり多くの学科合格者が出た理由は翌年の受験資格要件緩和以降にこのような状況を作るためだったと思われます。
試験元は緩和前年のR1年に「従来の受験資格要件を満たしていた学科合格者」を多く出すことで(かつ製図試験の難易度を上げることでストレート合格者のレベルは担保)「R2年の製図からの製図受験者数=R1年製図不合格者」を増やしたと考えられます。それによりR2年に増えることが間違いなかった「従来の受験資格要件を満たしていない学科合格者」の製図ストレート合格者を抑えています。また合格者数を維持しながら総合合格率の抑制にも成功しています。そして翌年以降も保留者含めて多くの製図受験有資格者がいることで学科試験の合格者数や製図試験の合格率をコントロールしていると思われます。
こうした見方は少なくとも緩和以降のここ数年の結果から矛盾のある話ではありません。そのため「試験元が製図受験者の上限値を想定している」という可能性は高いと考えています。
誤謬原因⑴「想定上限値11000人」
さて、以上のように「試験元が製図受験者の上限値を想定している」ことを前提と考えていましたが昨年はこの数字を「11000人」として、それがなぜ誤っていると今年は思っているのか、です。
昨年予想時と同じ考えですが試験元が製図受験者数を最もコントールできたのはR2年であったことは間違いないと思います。というのもR2年の製図試験受験者はR1年以前に学科合格した製図不合格者であり「製図は5年中3回受験可能」が適用されません。その為製図試験受験人数は減るとしても上記で触れた「辞めてしまったか不慮の事由による」少人数だけであり試験元が把握している人数に大きな変化はないはずだからです。製図受験者上限値を想定しているならばこの製図受験者数を引いた数字が学科合格者数(試験元が意図して設定することが出来た人数)となります。上限値の設定は上記のように学科合格者のレベル維持のためには必須と思えますし、何より(昨年もそれを理由として書いたが)実際問題としての試験会場の確保、採点官の確保、採点効率と正確性の担保等のためにも必要です。
この結果としての実際の製図受験者数が11035人だったわけですが、昨年は予想を進める際に見落としていることがありました。
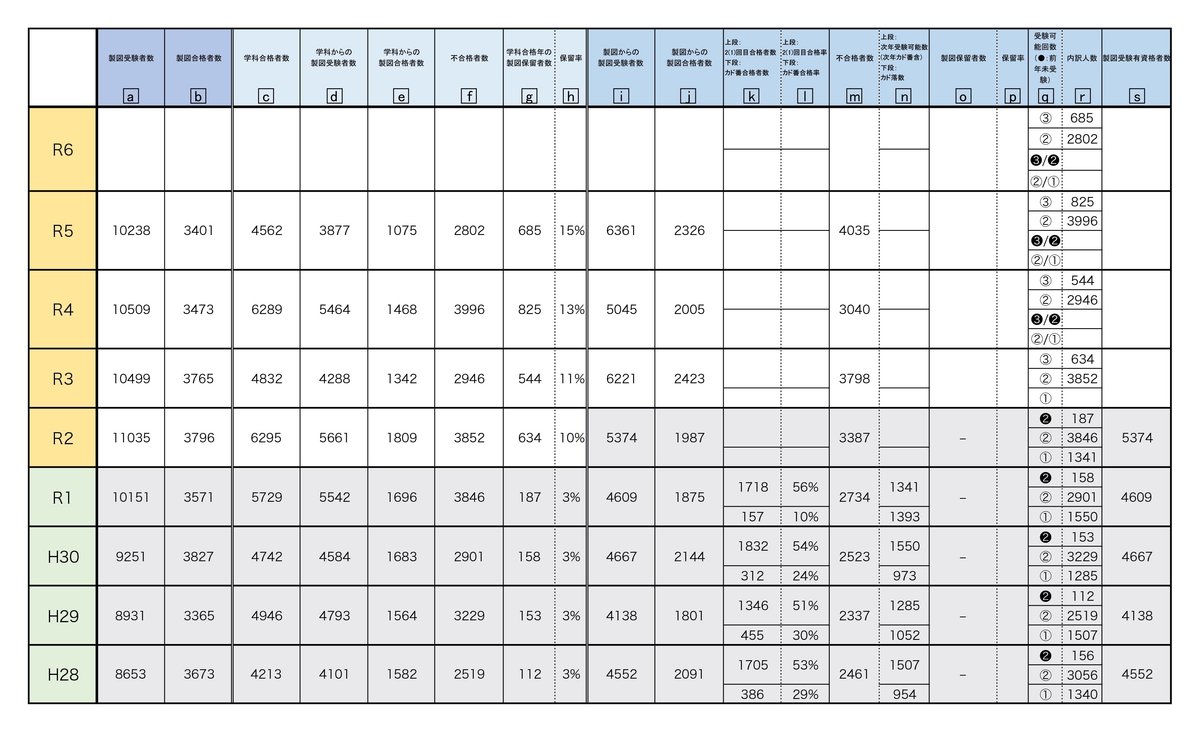
改めて表①(上記のものと同じ)を見ると緩和以前でも毎年3%と一定の製図試験保留者(h列)がいます。これは昨年記事内で推察した通り、「落ちていると思っていたが合格していた」ボーダー付近の合格者であり、製図の準備を全くしていなかった為回避した方達だと思われます(資格学校関係者等もいると思われるが誤差として無視しても良い少数と考えらえる)。これは緩和以前以後関係なく一定の割合として出ると考えられる数字であり、学科合格後に製図試験保留が可能になったR2年においても「少なくとも」発生する保留人数と考えて問題ないと思われます。
つまり少なくとも3%の製図試験保留者が出る前提で考えれば製図試験を受験する可能性があるのは最大でも学科合格者の97%となります。もちろんR2年はこれ以上の保留者が出ることは想定できますがその数字は推測不能である為試験元が根拠と出来る数字はこの3%しかなかったと思われます。
この推論からR2年に試験元が想定していた製図受験者上限値=6295人×97%+5374人=11480人≒11500人、となります(11500−5374/0.97=6315を上限として学科合格者数を設定→学科試験の難易度を設定したと考えられる)。
昨年はそもそも製図受験者11035人から11000人と想定したのですが試験元が(結果としての)10%の製図受験保留率を想定することは出来なかったであろうことを考えても全くの的外れな想定だったと言えます。
つまり上限値の設定があるとして、昨年予想は根拠に乏しいものであり、合理的な根拠を考えると500人のズレがあった、ということになります。
誤謬原因⑵「製図保留率7%」
昨年の予想が間違っていたもう一つの原因として製図保留率の誤りがあります。

表②として昨年の記事の予想内容を表①の空欄に入れてみました。
まず「カド番受験生の合格率は10%」として赤文字部が埋まります。流れとしてR2年「l列:10%」が決まれば=「k列」の数字が出て、「r列:カド番受験生数」ー「k列」=「n列:カド落数」が出ます。「m列」ー「n列:カド落数」=「n列:次年度カド番数」が出るのでそれがR3年の「r列:①」に記入できます。R3年の「r列」合計からR3年の「s列:製図受験有資格者数=6666人」が出ます。「s列」ー「i列」より「o列:製図保留者数」が出る、という流れです。昨年はここで「p列:445/6666=7%」として予想を進めていました(昨年記事では計算間違いにより445→455となっています)。ただよくよく考えるとR3年にカド番であると想定する「2180人」はR1年の学科合格者であり製図保留の権限がありません。つまり正しい「p列:製図保留率」は445/(634+3852)=10%ということになります(もちろんこれは「カド番受験生の合格率は10%」を前提とした数字)。つまりそもそもの計算の分母が誤っている為7%という数字は根拠のない間違ったものでした。
昨年の記事では「p列:7%」を前提に「o列」を計算、続けて青文字部の「i列」(「s列」ー「o列」)を出して試験元の想定製図受験者数とし、そこから緑文字の予想をしています(ここで学科合格者の製図保留率は10%を採用)。この計算の数字が「上限値:11000人」とした時に実際の学科合格者数とほぼ合致した為最初の「カド番受験生の合格率は10%」に妥当性が高いと判断したのでした。
まとめると⑴上限値11000人、⑵保留率7%という二重の誤りが⑶カド番受験生の合格率は10%でも矛盾しないという偶然の合致を招いたことが昨年記事の誤謬を生んだということになります。
では誤りであった⑴上限値11000人、⑵保留率7%をそれぞれ⑴上限値11500人、⑵保留率10%とした場合、⑶カド番受験生の合格率は10%に妥当性はあるのか確認してみます。

昨年記事と同じ流れでR4年学科合格者を出した所700人以上の差異が出ます。
このことからもやはり⑶カド番受験生の合格率は10%には妥当性がなく試験の動向を探る根拠にはなり得ないことがわかります。
R6年試験動向の推察
昨年「カド番受験生の合格率は10%」を前提に記事を書いたのは違和感がありつつも矛盾が生じなかったからです(上記の通り前提の誤りが偶々の合致を生んだ)。結果としてはある程度の目安になるとはいえ、人数も異なる個々の属性に応じた合格率を一律に定めているとは考えにくいというのが昨年の記事を含め改めて検証した正直な感想です。
試験元は確かな情報として製図試験有資格者数を把握しているはずなので製図受験者の上限値が定まっているならば単純な引き算で学科試験合格者数を設定する(=学科試験の難易度調整)ことが出来ます。このことから今年は「学科試験合格者から製図試験有資格者を逆算して出し、それを元にカド番人数等を予想→R6年の学科合格者数を予想」という形で試験動向を推察したいと思います。つまり昨年の「部分の仮定→全体の矛盾なしを確認」とは逆に「全体の仮定→部分の矛盾なしを確認」という方法で推察を試みる、ということです。
前提条件
改めて推察を進めるにあたっての前提を確認します。
❶:試験元は製図試験受験者数の上限値を設定している
これは上記で長々と書いたように学科や製図の合格者レベルの維持や実際的な問題から現状間違い無いのではないかと思います。
製図合格率や総合合格率に大きな変動がない中、学科合格者数と学科合格率がR3年〜R5年で大きく変動しているのも学科主体ではなく製図主体で試験を考えている証左の一つと考えられます。
またこの記事自体、この前提がなければ全く進まないという意味で不可欠な前提です。
❷:❶の上限値は11500人である
この根拠も上述の通りです。当然全く異なる数字が設定されている可能性もありますがここ数年の製図試験受験者数から妥当性は高いと考えています。またこの前提の前提として「試験元は少なくともR2年においては学科合格者の製図試験保留率:3%という数字を採用している」という事柄があります。
推察⑴
「学科合格者の製図試験保留率:3%」
まずR2年では製図試験の保留率は3%として学科合格者数を決めていた、という前提から始めているので翌年R3年以降も同様の「保留率:3%」で試験元が学科合格者を決めているという仮定で諸々の数字を確認したいと思います。

試験元が把握している数字は「s列」なので、
(11500ー「s列」)/97%=「c列」
という計算から学科合格者数を設定していると想定されます。
結果として「c列」の数字がわかっているので、ここから逆算して
「s列」=11500ー(「c列」×97%)となります。
「s列:製図受験有資格者数」が計算出来たので実際に受験した人数「i列」の数字を引いて「o列:製図受験保留者数」および「p列:保留率」が算出出来ます(赤文字)。
R3年は「s列:(6813)」から「r列」の前年保留者(634)、前年製図不合格者(3852)を引くことで「カド番受験者数(2327)」が分かります。R4年、R5年については「o列:保留者数」が「q列」の翌年の「❸/❷(または❸/❷/❶)」に入り(赤矢印)、前年保留者、前年製図不合格者を合わせて「s列」から引くことで「カド番受験者数を含む前年製図不合格者」が分かります(青文字)。
この数字は前年の「n列:カド落以外の製図不合格者数」のことなので(青矢印)、「m列」からこの数字を引くことで「n列:カド落数」が分かります。
ここまで表を埋めてR3年に着目すると「カド落数(2480)」>「カド番受験者数(2327)」となっており受験者数より不合格者が多いという明らかな矛盾が生じます。
つまり毎年「学科合格者の製図試験保留率:3%」として学科合格者数を設定している、という仮説は誤りである、ということが言えます。
推察⑵
「学科合格者の製図試験保留率:前年度実績」
毎年同じ保留率で学科合格者数を想定しているわけではない時に考えられるのはR2年以降の「製図は5年中3回受験可能」という条件により変化している保留率の採用です。学科合格年の製図保留率は正確にわかる数値ですが前年の実績を元に考えるということはおかしなことではありません。
推察⑵では前年度実績を前提に数字の確認を行いたいと思います。

「c列」に乗算する数値を前年の保留率から得られる数値として推察⑴と同じ手順で表内を埋めて行きます。
「n列」の不合格者内訳まで見ても明らかな矛盾がない為さらに進めて「k列」の合格者内訳と「l列」の合格率を計算します。「r列:カド番受験者」ー「n列:カド落数」=「k列:カド番合格者数」が出ます。「j列:製図合格者数」ー「k列:カド番合格者数」=「k列:カド番以外の合格者数」が出せます(緑文字)。
R4年については「r列:②/①」の表記からもわかるかと思いますが、1483人中にカド番になった方と1回保留後に受験して不合格になったまだ2回受けることが出来る方が混在している為、単純な計算でカド番受験者数が出すことが出来ない為空欄としています。
ここでR2年の「l列:合格率」に着目するとそれまでとは明らかに異なる傾向が読み取れます。推察⑴のような明らかな矛盾ではないもののかなり違和感のある数字です。製図受験2回目の方の合格率が15〜20%下落している一方、カド番受験生の合格率が15〜20%上昇しています。
読んでくださっている人の中に該当する方がおられて気分を害されたら申し訳ないのですが、R2年の製図受験2回目の方の合格率が例年と比較して下落することに関してはある程度の説明が出来ると思っています。R2年製図2回目=R1年学科合格者です。R1年学科合格者には上記のように試験元が「翌年以降の製図受験人数をコントロール」するために「あえて増やした」方々も含まれます。つまり「例年であれば合格水準に達しない=例年ならば試験元が製図受験能力有りと認めていない」方も合格していたと考えられるからです。その為例え2回目であっても製図において学習量や取り組みが合格する方々の平均に満たない方がいても不思議ではなく不合格になる方が多くなったと思われます。ただ、そうだとしても下落の幅としては大きすぎると感じられます。
一方でカド番受験生の合格率がここまで大きく上昇することについては説明がつきません。カド番合格者数で見ても600人超えと例年の水準を大きく上回っていますし、R2年にカド番となるH30受験者の最終合格率(結果的に合格した人の割合)が85%と、これまで80%を超えていない数字が5%も上昇するとは考えにくいです(この場合R3年にカド番となるR1受験者の最終合格率60%、例年77〜80%)。
またR3年の「p列:製図保留率」=21%は前年に同じ集団の製図保留率が10%(R2年「h列」)であることを考えると上昇しすぎであると感じられます。
こうした数字から、前年度実績を採用して学科合格者を設定しているという推察も妥当性があるとは言えないと思われます。
※以下、推察⑶では妥当性があると考えられる仮説とその検証を示しています。またその仮説を元にR6年製図試験有資格者数やR6年学科試験の合格者数およびそこから考えられる内容を予想しています。
※有料部分となりますがXで該当ポストをリポストして頂くことで全て無料でお読みいただけます。よろしくお願いします。
ここから先は
この記事が気に入ったらチップで応援してみませんか?
