「大数の法則」をわかりやすく（その１）

機械学習やデータサイエンスの応用でも時々顔を出す数学。これをなるべく正確に、でも分かりやすく説明するのがこの記事の目的です。

今回は統計を使うときには避けられない大定理、大数の法則を分かりやすく説明してみたいと思います。

というのも、この大数の法則、なんとなく分かった気にはなれますが、ちゃんと理解しようとして数学の本を開いてみるとなんだか３つくらいあるんですよね。

大数の弱法則とか大数の強法則とか、はたまた確率収束だとかほとんど確実に収束だとか――

雰囲気をつかむことはできてもきっちり理解するのは意外と大変な大数の法則。

今回はこれらの用語と、もちろん大数の法則自体も分かりやすく説明したいと思います。

データサイエンス・機械学習のモチベーション

そもそもデータサイエンスや機械学習というものは何を目指しているのでしょうか。

実はデータサイエンスも機械学習もやりたいことはとってもわかりやすくて、要するにこんな感じ。

この「真の分布」ってやつは人間の手には届きません。なにしろ本当にあるのかもよくわからない神様みたいなものです。

つまり、

という感じ。

このオレンジの線より上のことは人間にはわかりません。

そこでなんとかして、完全に「真の分布」と同じでなくていいからサンプルの情報からなるべく似ている「モデル」をつくりたい。

それがデータサイエンスや機械学習のモチベーションです。

ぼくは最初同じような解説を聞いたときに「統計学と何が違うんだ？」と感じました。

ひとことで言うなら、「手で書く数式で処理しきれなくても、パソコンのすさまじい計算力で無理やり答えに近づこう」ってやるのがデータサイエンスや機械学習だ、と理解すればよいようです。

というか統計学の一分野と思ってしまってもだいたい大丈夫みたいですね。

大数の法則とは

それではなんとなくモチベーションをつかんだところで、大数の法則ってどんな定理だっけ？　ということを確かめたいと思います。

いま私たちの望みとしては「真の分布の情報をサンプルの情報からなるべく正確に読み取りたい」というものでした。

真の分布の情報を知れば知るほど、その現象の理解が深まるわけです。

ところで、真の分布に関してこれだけは譲れないというめちゃくちゃ大切な情報を一つ選ぶとしたら何でしょうか？

それは、平均です。

平均というのはその分布がどこを中心に広がっているのかを表すものすごく大切な量です。

ですから、我々はサンプルの情報から何とか真の分布の平均を知りたいわけです。

そう思った矢先、なんと次のようなことが成り立つということがわかります。

簡単に言ってしまえば、

「サンプルの平均が従う分布」の平均はもとの「真の分布」の平均と等しい

ということです。

Xの上に棒が乗ってるのは「エックスバー」と読んで、標本平均（＝サンプルの平均）を表します。サンプルの平均ですから、さっきの図でいうと下の世界の平均ですよね。

ここ、つまずきますよね。

初めて聞いたときにはぼくは意味が分かりませんでした。

これを理解するためには、確率変数同士は足しても確率変数、ということに注意してもらいたいです。

そのうえで、

エックスバー（サンプルの平均）もまた、新しい確率変数だと思えるのだ

ということを強く意識してください。

新しい確率変数なので、どんな謎の分布に従っているのかはよくわかりません。でも、その謎の分布の平均はもとの分布の平均と同じだ！　ということがわかってしまったんです。

それではこの調子で，エックスバーの分散も求めてしまいましょう。

数式苦手orとりあえず結果知りたい方は計算結果だけ追っていただいても大丈夫です。

少し大変ですが一気に行っちゃいましょう。

いろいろ計算しましたが、結果的に最も大切なのはこれです。

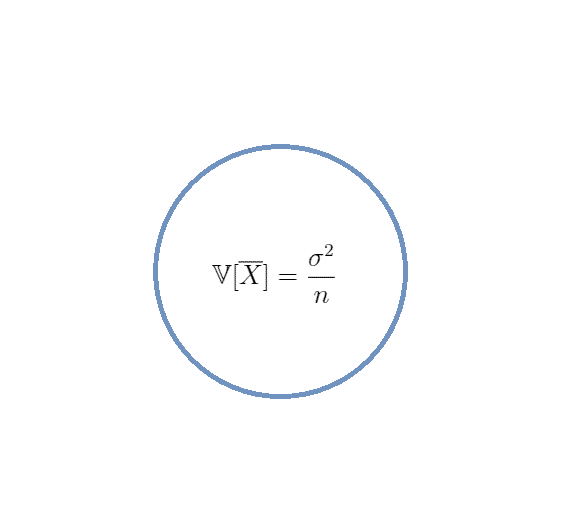
ということで，分散は平均と違ってもとの分布と同じにはならないことがわかりました。

しかし，よくこの形を見てみるとあることがわかります。

「サンプル数nが大きくなると，分散はどんどん小さくなる！」

ということがわかるんです。すなわち，

「サンプルの平均は真の分布の平均にどんどん近くなる！」

ということです。

イメージはこんな感じ。

つまり、サンプル数が膨大な数字であったらサンプルの平均と真の分布の平均はほぼ同じものだと思っていいよ、ということです。

しかも、真の分布がどんな分布であってもです！

というわけでめでたく真の分布の平均を知るめどが立ちました。

これこそ大数の法則のだいたいのイメージです。

というわけで今回は大数の法則のイメージをつかんでもらいました。次回はこの事実を数学的にもう少しきっちり見てみます。