
量子力学の解釈問題
量子力学は,原子に相当するようなきわめて小さいスケールにおいて,物質を構成する粒子や光などの振る舞いを記述する理論です.
ミクロなスケールでは,物質は私たちの日常生活にもとづく常識とは大きく異なる性質を示すことが知られています.そのひとつが,波と粒子の二重性です.ミクロな物質や光は,波の性質と粒子の性質を併せ持つというものです.また,ミクロな物質や光は,同時に複数の場所に存在することができ,状態の重ね合わせとして表されます.
そんな不思議な性質を示すミクロな世界を記述する量子力学において,標準的な考え方の一つとされるのがコペンハーゲン解釈です.ただ,コペンハーゲン解釈にはまだ議論の余地のある未解明のメカニズムが含まれているとされていて,その問題を解決できるかもしれない考え方の一つが多世界解釈です.今回は量子力学のコペンハーゲン解釈と多世界解釈について紹介していきます.

コペンハーゲン解釈
電子が波の性質を持つことは,いわゆる二重スリット実験から示されます.二つのスリットに向けて電子を一つ打ち出すと,その先のスクリーン上で電子はある一点で観測されます.その結果だけを見ると,電子は単純に粒子として振る舞っているように思われます.

では,この実験を何度も繰り返していくとどうなるでしょうか.もし電子が単に粒子の性質しか持たないのであれば,スクリーン上では電子の発射元と二つのスリットの延長線上のあたりだけで,電子が観測されると期待されます.しかし実際は,二つのスリットに向けて繰り返し何度も電子を発射していくと,スクリーン上にはしだいに縞模様が現れてきます.そしてその縞模様は,二つのスリットで回折した波が干渉したと考えるとうまく説明できます.このことから,二重スリット実験の結果は,電子が波としての性質も持つことを示唆していると言えます.

波と粒子の二重性とは,どのように理解すればよいのでしょうか.二重スリット実験の結果から示唆されるように,電子の振る舞いを理解するためには,スクリーン上で観測する前の状態の計算と,スクリーン上で観測した結果に関する計算を区別すると良さそうです.スクリーン上で観測する前の電子は,たとえ一個だけであっても二つのスリットで回折した波として振る舞うことから,広がった波として解釈する必要があります.一方,観測された電子は一個の点として現れますから,粒子として解釈する必要があります.
ドイツの物理学者マックス・ボルンは,電子の広がった波は,電子の発見確率と関係しているという考え方を提案しました.電子は波として広がって存在していて,電子の波の振幅の大きい場所ほど電子の発見確率が高いと考えるわけです.こうした考え方を確率解釈と呼びます.

二重スリット実験において,発射された電子は二つのスリットを通過して二つの波となります.二つの波は干渉しながらスクリーンへと向かい,その結果スクリーン上では電子の発見確率の高い場所と低い場所が干渉縞のように交互に生じます.電子をひとつ発射すると,その電子はスクリーン上のある一点だけで観測されます.このとき,スクリーン上で電子の発見確率の高い場所ほど,電子が発見されやすくなります.そのため,たくさんの電子を発射していくと,電子の発見確率の高い場所ほどより多くの電子が観測されることになり,しだいに干渉縞が浮かび上がることになります.

また,スクリーン上で観測される直前までは,電子の波はスクリーンいっぱいに広がっていますが,スクリーンで観測された瞬間に,電子の波は1点に収縮して粒子として観測されると考えることができます.波の収縮と呼ばれます.そして,こうした波の収縮と確率解釈を基本として量子力学を正当化する考え方を,コペンハーゲン解釈と呼びます.コペンハーゲン解釈はさまざまな観測事実と矛盾しないため,量子力学の標準的な解釈とされています.

電子の波は,数学的には波動関数と呼ばれる関数で表されます.オーストリアの物理学者エルヴィン・シュレディンガーは,波動関数の変化を記述する方程式を導きました.シュレディンガー方程式と呼ばれます.実用的には,シュレディンガー方程式を用いれば,電子の発見確率を計算することができ,それらの振る舞いを詳しく知ることができます.
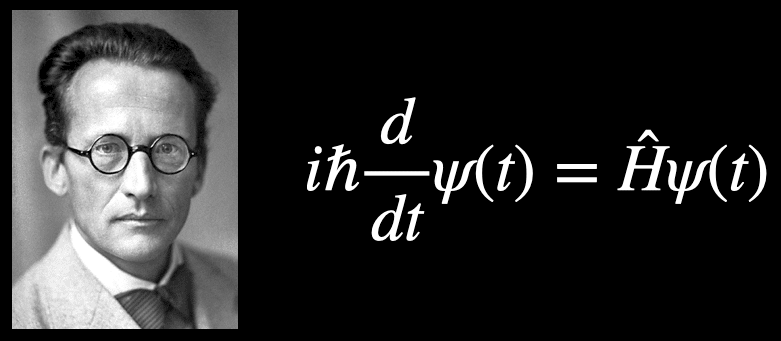
ただ,コペンハーゲン解釈では,そもそもなぜ観測されると波の収縮が起きるのか,収縮前に広がっていた波のうち,観測されなかった部分はどこへいってしまったのか,といった根本的な問題に答えることはできません.こうした問題の本質は,そもそも電子の波とはどういうものであるのか,そして電子はどのような意味で粒子であるのか,といった認識自体にある可能性があります.
多世界解釈における波動関数の意味
この問題に対して新しい視点を与えたとされるのが,1957年にアメリカの物理学者ヒュー・エヴェレットによって提案された多世界解釈です.

コペンハーゲン解釈では,電子の波は観測されると一点に収縮すると考えます.このとき,電子の波は実在しているわけではなく,確率的に観測結果を計算するための数学的な手段であると捉えます.もともと電子の波は実在しているわけではないので,突然なくなってしまっても構いません.そもそも観測されないものについて,存在の有無を論じるのは非科学的発想であるという主張もあります.
これに対して多世界解釈では,電子の波は実在の表現だと考えます.ただし,電子の波が実在しているというわけではありません.電子の波は,実在する電子の複数の状態が共存する様子を,共存度の分布という形で表すものと解釈します.

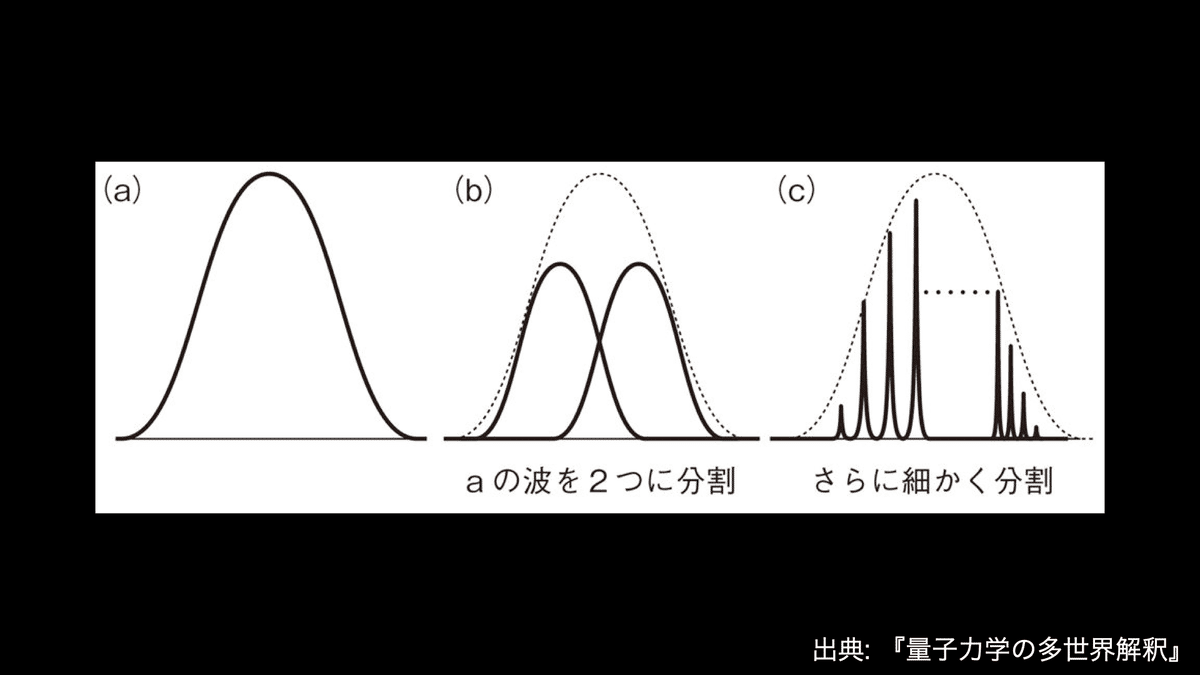
波は互いに重なるとき,単にその高さを足し合わせればよいという性質を持ちます.重ね合わせの原理と呼ばれます.重ね合わせの原理をもとにすると,広がっている波は,たとえば左右に分かれた二つの波の重ね合わせで表すことができます.
この分割を細かくしていくと,広がっている波は,位置が完全に決まっている幅の狭い無数の波の重ね合わせとみなすことができます.つまり,電子の波というものは,位置の決まっている無数の波が共存しているものと解釈できるというわけです.このとき,電子が多数あると言っているわけではなく,一つの電子が同時にいろいろな位置にあると言っているわけでもありません.電子がいろいろな位置にあるという状態が多数共存しているという考え方をするわけです.
そして,そうした状態の共存の様子を表すのが波動関数であると考えます.波動関数の各点での値は,電子がその点に存在する状態の共存度に対応しています.
状態の共存とデコヒーレンス
多世界解釈にはもう一つ大きな特徴があります.それは,電子のようなミクロな対象だけでなく,観測装置やそれを用いる観測者といったいわゆるマクロな対象も含め,すべてが量子力学の対象であると考えるというものです.
量子力学がこの世界の根本原理であるならば,原子や電子といったミクロな粒子だけでなく,それらから構成されるマクロな物体や人間,さらには宇宙全体も同じ原理で説明されるべきである,という発想です.それにしたがうと,原子や電子のようなミクロな粒子だけでなく,それらを観測する観測者も共存する状態の中にいると捉えることができます.

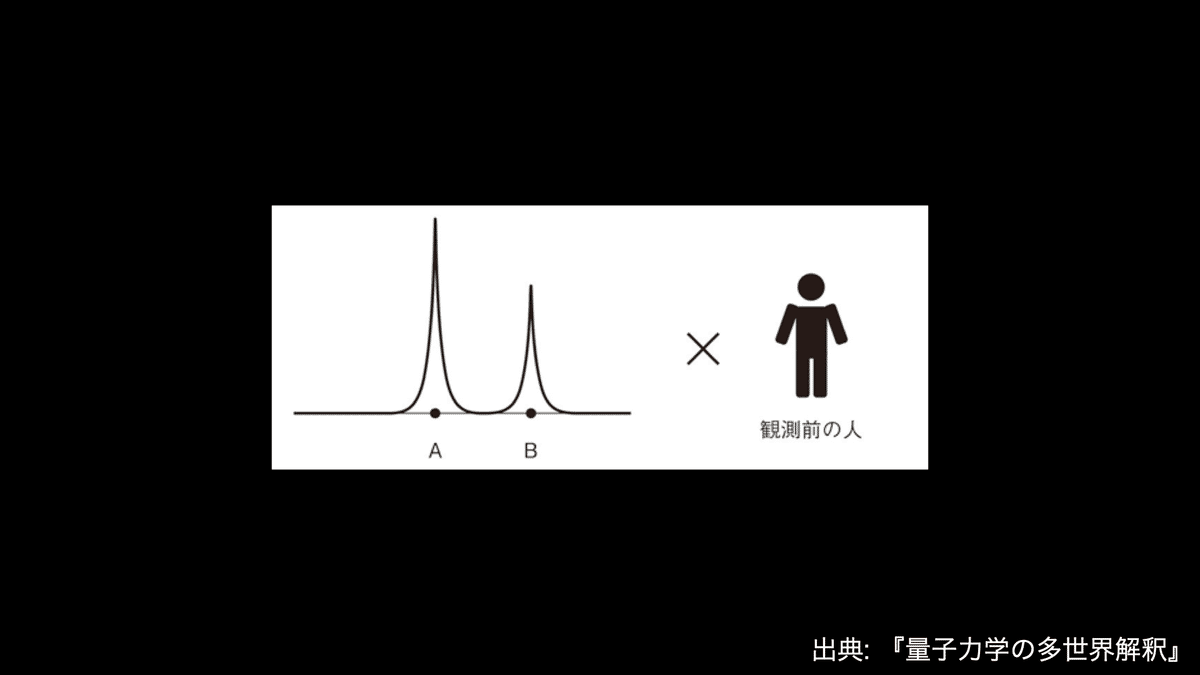
簡単のため,電子の波を単純化して,電子が位置Aと位置Bという二箇所の位置にある状態が共存しているとします.電子の波がAとBの二箇所にだけピークを持っているような状況です.そしてこの電子を観測者が観測することを考えます.コペンハーゲン解釈では,観測者はこの電子の波の外にいて,観測によって電子の波はどちらか一つに収縮すると考えます.

一方,多世界解釈では,観測者自身がこの状態の中にいると考えます.電子が位置Aにある状態の中にも,位置Bにある状態の中にも,どちらにも観測者がいる,と捉えるわけです.このとき,観測者は位置Aと位置Bのどちらでも電子を観測しうる状態にあります.そのため,観測者を共通因子としてくくると,電子が位置Aにある状態と位置Bにある状態は互いに干渉することができます.
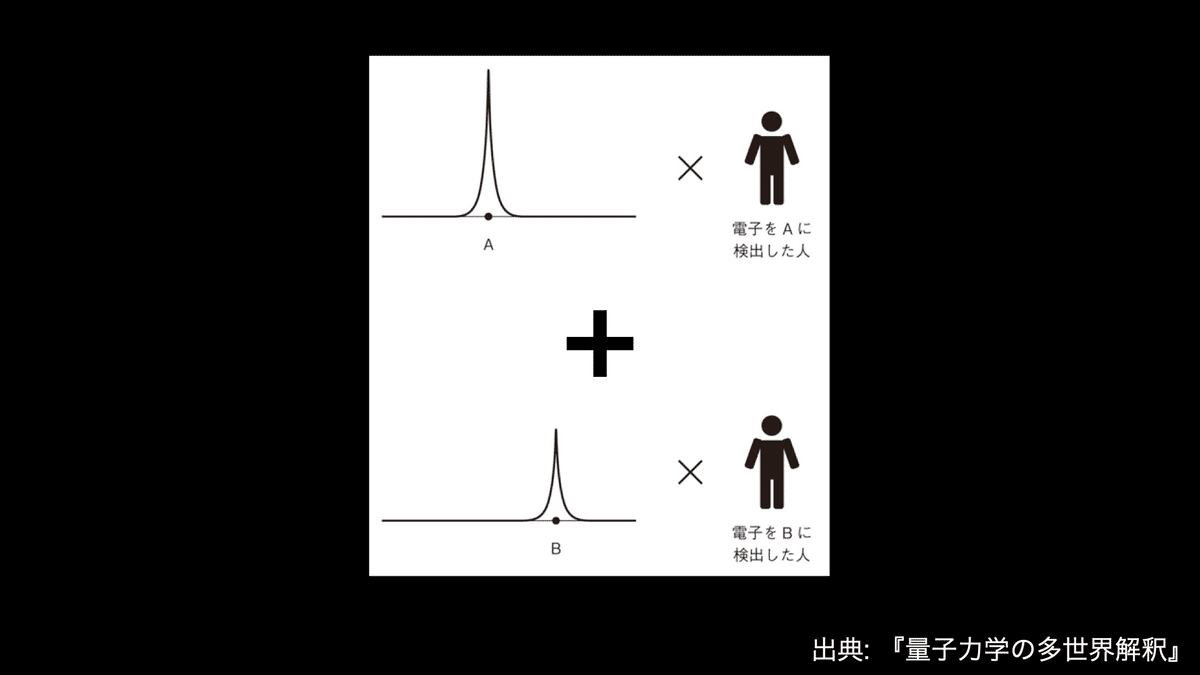
これに対して,観測者が電子を観測すると,電子が位置Aにある状態では,観測者は電子を位置Aに検出した観測者となります.電子が位置Bにある状態では,観測者は電子を位置Bに検出した観測者となります.観測によって,観測者側にその記録が残るわけです.いったん観測してしまうと,同時に位置Aと位置Bに電子を観測することはありえません.なぜなら,位置Aと位置Bの両方で電子を検出したという観測者の状態がないためです.観測者が電子の位置を観測すると,状態全体としては,電子がAに検出されたという世界と,Bに検出されたという世界の,二つの世界の足し算になります.このことはこれらの世界が共存していることを表しています.
観測前は,電子がAにある状態とBにある状態が共存していて,これらは互いに干渉することができました.では,観測後の共存している状態は,互いに干渉してしまわないのでしょうか.もし干渉するとしたら,実用的にはうまくいっているコペンハーゲン解釈と結果が食い違ってしまうように思われます.
実は,観測装置を使った観測など,無数の原子が関係するマクロな現象が起きると,それらの状態の間に修復不可能な違いが生じて干渉効果が生じなくなります.デコヒーレンスというメカニズムによるものです.

多世界解釈では,異なる位置に電子が観測されたという状態が,収縮を起こさずに共存し続けると考えます.これを「世界が分岐した」と表現します.それらの状態が干渉しないのであれば,波の収縮というメカニズムを導入する必要はないわけです.

多世界解釈は,コペンハーゲン解釈で仮定される波の収縮というメカニズムを排除して,ミクロな物理現象を説明しようとする考え方の一つです.世界の分岐によってデコヒーレンスされた複数の世界が多数共存していることを示唆するため,直観的には理解されにくく,サイエンス・フィクションのような印象を持たれてしまうこともしばしばです.観測できない世界を持ち出すのは論理の無駄であると批判されることもあります.

これまでに構築されている量子力学は,ミクロな物理現象に関するさまざまな実験結果や観測結果をうまく説明できているため,実用的にはどちらの解釈でも構わないという側面はあります.ただ,解釈問題に対する議論を経て,新しい物理学のインスピレーションが得られたり,私たちの存在しているこの世界に対する理解が深まったりすることがあるかもしれません.そもそもこうした問題が生じてしまうのは,さらなる大きな理論的な枠組みが必要であることを示唆しているのかもしれません.今後,物理学がさらに進展し,量子力学の解釈問題が明解に解決されることを期待して,この動画を締めくくりたいと思います.

参考文献
量子力学の多世界解釈
https://amzn.to/3yOa4mE
