【因子分析】因子負荷の最尤法は実は賢い

こんにちは、Aska Intelligenceの川本です。

因子分析（Factor Analysis）の因子負荷推定において、最尤法は最もメジャーな方法だと言われています。最尤推定は、統計モデルが書き下せればお決まりの手順で解が求まるものと思われがちかもしれません。

もちろん最尤解が満たす方程式（極値条件）は解析的には解けない場合が多いので、数値的に解を求めるのが難しいという話はあります。

ただ因子分析の最尤法はそれだけではなく、実は定式化において少し賢いトリックが入っているのでそれをご紹介します。

因子分析モデル

まずは記号を整理するために、因子分析モデルをおさらいしましょう。因子分析モデルは、$${p}$$個の観測変数を持つデータ $${\bm{x}}$$ （$${p}$$次元ベクトル）に対して

$$
\bm{x} = \bm{f} \Lambda^{\top} + \bm{e}
$$

という式で表現されます。因子数を$${k}$$とすると、$${\bm{f}}$$は$${k}$$次元ベクトルの因子得点（もしくは共通因子）、$${\Lambda^{\top}}$$は$${k \times p}$$行列の因子負荷行列です（$${\top}$$は行列の転置）。$${\bm{e}}$$は$${p}$$次元の乱数ベクトルで、独立因子や残差と呼ばれているものです。

$${\bm{e}}$$の各成分は期待値がゼロの独立な乱数で、共分散行列が$${p \times p}$$行列$${V}$$で与えられるとします。$${V}$$はデータから推定する対角行列です。

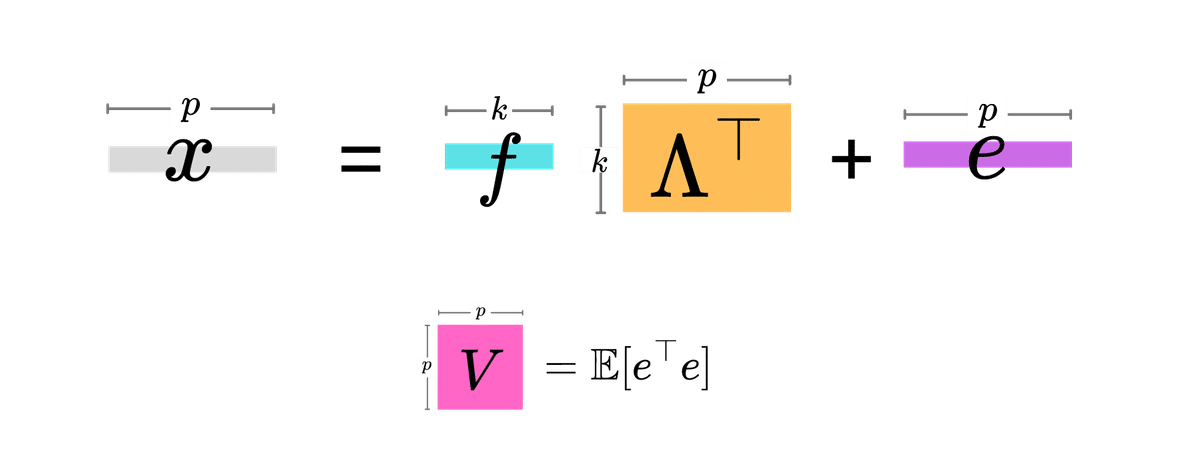
他の記事で紹介したように、因果分析モデルには$${\bm{f}}$$をパラメーターとするバージョンと乱数とするバージョンがありますが、ここではあまりその差は顕在化しません。パラメーターとして扱っても良いのですが、その場合に真面目に最尤法を考えると、実は最尤法が破綻している問題にぶち当たってしまうので、ここでは$${\bm{f}}$$は乱数ベクトル（つまり推定しなくて良い量）としておきます。

最尤法

$${\bm{e}}$$の各成分が正規分布に従う乱数だとすると、$${\bm{x}}$$についての確率分布が書き下せます（別に正規分布でなくても良いはずですが、正規分布が数学的に扱いやすいのでそう仮定します）。

$${\bm{x}}$$は確率変数ベクトルですが、ここに実際の標本データの値を代入し、モデルパラメーターの関数と解釈し直したものが尤度関数です。この関数を最大化するようにパラメーターを最適化するのが最尤法でした。

ただ、この段階で（対数）尤度をパラメーター微分して極値条件を出しても最尤解は一意に定りません。因子の回転自由度が残っているからです。

因子分析モデルには、因子回転の不定性があります（ここでは説明しませんが、これを読んでいる人は聞いたことはあると思いますので、飛ばします）。

因子回転を最終的にどう決定するかは重要な問題ですが、今は初期解を求めているので、解きやすい条件を自由に入れて大丈夫なのです。「とりあえず解を初期解として１つ出しておき、回転自由度はその後調整する」というのが因子分析の通常の手順だからです。

ここで導入する制約条件にはいくつか有名なものがありますが、最もメジャーなのが

$${\Lambda^{\top}V^{-1} \Lambda }$$の推定値は対角行列である

という条件です。単位行列ではなく、対角行列であるという条件です。これを最初に導入したのはLawleyという人らしいです。

なぜこの条件を与えると都合が良いかというと、解が尺度不変性（スケール不変性）を持つからです。よく「最尤法は尺度不変性を持つことが利点だ」と説明されることがありますが、正確には「この条件を導入した最尤法が尺度不変性を持つ」のであり、最尤法であれば勝手に成り立つ性質ではないのです。

ということで今回は、実は最尤法は尺度不変性を持つように賢く定式化されているということをご紹介しました。ここではお話レベルでざっくり説明しただけですが、数式でちゃんと理解したい方は、Zennの本に書いてありますので、興味がある方は買ってみてください。

---

因子分析についての入門資料はウェブ上に膨大にありますし、入門書やセミナーもたくさんありますが、ちゃんと数式を使って中身を説明したものはあまりないので、「ちゃんと公式を導出して理解する本」をZennで書きました。

因子分析の導出 -古典的な方法の理解のために-