【ポケカAdvent Calendar2024】確率から考えるたねポケモンの採用基準【13日目】

Yua

本記事はいちょーさん主催のポケカアドカレの13日目の投稿記事になります

前日のともぽんの記事はこちらから

まえがき

ポケカアドカレも3年連続の出場となりました、下野です。
こいついっつも抽象的なことしか言わんやんけ、と思われてそうなのでたまには具体的なお話をしようと思います。

今回は確率からたねポケモンの枚数を考えてみようのコーナー。
自分が実際シティリーグS1で使ったイバラドラパルトのデッキを題材にします。
イバラドラパルトは現スボミー環境でも注目されているデッキの1つですので、前環境の考察とはいえ少しは参考になる情報もあるのではないかなと思います。

ちなみに先に言っておくと散々こねくり回した結果普通に1回戦から8ターンくらいパスして結果は惨敗なんで、これが正しい考えた方とかそう言うつもりは無いです。

いつも通り考え方の1つとして参考にしていただけると幸いです。


たねポケモンについて

必須枠と自由枠

自分が出場した超電ブレイカー発売直後はタケルライコオーガポンの数が多いことが予想されたのもあり、キリンリキを含む以下のポケモンが確定枠とされていました。

  • ドラメシヤ - 4枚

  • テツノイバラex - 4枚

  • キリンリキ - 1枚

  • かがやくフーディン - 1枚

この確定の10枚を基準にたねポケモンを増やす(あるいは減らしたりする)ことを考えます。
増やす候補のカードは以下の2枚です。

  • シャリタツ

  • クレッフィ

これらのカード群を増やした時にデッキとしてどういう意味を持たせられるのかを考えます。

自由枠カードの役割

シャリタツ
イバラドラパルトというアーキタイプは、適切なターンに適切なサポートを打つことが重要になるデッキです。
1Tにはプレシャスキャリーとエヴォリューションを持ってこれるペパー。
2Tにはテツノイバラexが技を打つためのエネルギーを供給するアカマツ。
それ以降のターンでは状況次第でアカマツ、ボスの指令、ナンジャモを使い分けて打つことができれば非常に強力です。
シャリタツを採用すれば、このデッキで重要な要素の1つであるテツノイバラexでのスタート率は下がってしまいますが、それ以外の強い動きの再現性を大きく高めることができます。

クレッフィ
クレッフィは少し弱いテツノイバラexの役割を果たします。
ピジョットexやリザードンexの特性は止められませんが、ロトムVやイキリンコex、オーガポンみどりのめんexの特性を止められるこのカードは、一定のアーキタイプに対してテツノイバラexと同等の役割を果たします。
コイントスで後攻を選択するイバラドラパルトのデッキ性質上、テツノイバラex以外のポケモンでスタートした際に、ボール等の手段から逃げて前にテツノイバラexを置いて1Tから特性ロックが出来ない以上、特性ロックできるポケモンでのスタート率を向上させることには大きな意味があります。
ただしテツノイバラexと違い、このポケモンで1Tにエヴォリューションを打つと、2Tにアカマツがあったとしてもテツノイバラexでわざを宣言できないため、特性ロックで相手を止める代わりに自分のゲームスピードも遅くしてしまうというデメリットがあります。

スタート率を計算する

計算式

計算式は探せばいくらでも出てくると思います。
自分は適当にpythonで計算してます。実装は3秒で終わるレベル。

import math

## combinationの実装
def comb(n,r):
  return math.factorial(n) / (math.factorial(n-r) * math.factorial(r))

## 初手にx枚のたねポケモンがある確率
def calc_no_mulligan_rate(x):
  return 1-comb(60-x,7)/comb(60,7)

## たねポケモンx枚のデッキで特定のカードa枚でスタートできる確率
def calc_starting_rate(x,a):
  return (1-comb(60-a,7)/comb(60,7))/calc_no_mulligan_rate(x)

## ex.たねポケモン10枚のデッキで、4枚のテツノイバラexでスタートする確率
calc_starting_rate(10,4) # 0.5388661709180262

## ex.たねポケモン11枚のデッキで、4枚のテツノイバラexまたは1枚のクレッフィでスタートする確率
calc_starting_rate(11,5) # 0.610307452853742

これ見て「クレッフィを入れると7%も改善するんだすごい！！！」
……では計算に何の意味もありませんよね。

確率をどう使うか

「～をすると××の確率が◯◯％を超えるから、～をすべき」という理論をために見ることがありますが、◯◯%を超えると何故良いのでしょうか。
その根拠がなければこの理論には意味がありません。

今回の例も同じです。
53%はなんとなく嫌だけど60%を超えるとまあまあやれる気がする、では気分は良くなるかもしれませんが決して論理的とは言えません。

では確率をどう使えば良いか。
その1つの回答として、スタート回数の期待値と自分の期待勝率とを照らし合わせて考えるという例を紹介します。

スタート回数の期待値

シティリーグの予選を例に考えます
予選は6回戦あるので6回中何回特定のたねポケモンでスタートできるかを計算してみます。
実装はさっきより超簡単なので1秒。

## n回中m回特定のポケモンでスタートできる確率 
def N_out_of_M(n,m,starting_rate):
     return (starting_rate**m) * (1-starting_rate)**(n-m) * comb(n,m)

## 6連続
N_out_of_M(6,6,0.5388) # 0.02446614370592201

## 6回中5回以上
N_out_of_M(6,6,0.538) + N_out_of_M(6,5,0.538) # 0.1501207704004792

## 6回中4回以上
N_out_of_M(6,6,0.538) + N_out_of_M(6,5,0.538) + N_out_of_M(6,4,0.538) # 0.4190142087427666

というわけでざっくり計算ができたところで比較してみます。

クレッフィありor無しの比較

確実に決勝トーナメントに進むために必要な5勝を考え、5回以上特定のたねポケモンでスタートできる確率を比較すると約25%と15%と10%の差があります。
この差をどう考えるべきでしょうか。

考え方の1つとして期待勝率を考えるという手段があります。
簡単のために
・テツノイバラexまたはクレッフィでスタートした試合の勝率：100%
・それ以外のポケモンでスタートした場合の勝率：0%
とすると、クレッフィを採用しても勝率は25%となります。
例えば年に1回シティリーグの予選を抜けることをが目標ならこれで十分なな可能性もありますが、2回に1回や4回すべて抜けることを目標とする場合、全く足りていないことは明白です。

つまり、クレッフィを採用しても高々25%なのだから、そもそもスタート率の改善でデッキの勝率を向上させようというアプローチが間違いだということを示してくれます。

逆に言うとシティリーグでイバラドラパルトというアーキタイプで予選を突破するのに必要な要素はテツノイバラex以外でスタートしたときの勝率をどう担保するか、という点に集約されます。
現実的な問題として、6回戦のうち2-3戦はテツノイバラex以外でのスタートする前提で考えたときそのうちの少なくとも1戦は勝利する必要があり、その場合の勝率50%が切るようならばこのデッキは要求を満たしていないと言えます。

またもう少し具体的な考え方をするのであれば、クレッフィというカードが主に有効なロトムV、イキリンコex、オーガポンみどりのめんexを採用するデッキのうち、クレッフィの特性ロックが特に強いのはタケルライコオーガポンのみです。
ロトムV採用のリザードンやドラパルトは無理やり進化されて後続が無いパターンでもこちらが有効な返し手段を持っておらず、ロックに拘らず純粋なドラパルトデッキとして進行した方が抗える試合が多かったり、後者2つを採用するレジドラゴデッキに対しても、2Tにレガシースター+プライムキャッチャーorボスの指令からロック解除＋トライフロスト等から瞬殺されるおそれがあります。
タケルライコオーガポンには確かに多くの場合で有効ですが、そもそもタケルライコオーガポンに対しては必殺のリキキリンexが採用されているため、必要な場面は
・"6回中2回以上テツノイバラでスタートできない"
・かつ"その対戦相手が対ケルライコオーガポンである"
・かつ"その試合をクレッフィでスタートできている"
・かつ"キリンリキまたはリキキリンexがサイド落ちしている"
という状況ですので、いかにその場合の勝率が100%であろうが総合勝率にはほとんど影響しないということは計算せずとも明白でしょう。

余談ですが、ヒスイのヘビーボールの採用についても同様です。
そもそもタケルライコオーガポンに対して先攻1Tからの特性ロックが一定の勝率を担保していることから
・"対戦相手がタケルライコオーガポンである"
・かつ"テツノイバラexでスタートしていない"
・かつ"ヒスイのヘビーボールがサイド落ちしていない"
・かつ"エネルギーまたはヒスイのヘビーボールが手札にある"
・かつ"キリンリキがサイドに落ちていてリキキリンexがサイド落ちしていない"
時に有効なカードであるため総合勝率にはほとんど影響しないカードであり、採用に価値が無いと言えるでしょう。

条件によって変わる

これまで議論はシティリーグという場に限定したものでした。
例えば10000戦のレート戦の戦績を同様の勝率で仮定すれば、スタート確率である54%と61%という差がそのまま勝率の差に表れます。

また極端な例を考えるならタケルライコオーガポンの使用率が100%と仮定するなら、先程微差だと切り捨てた総合勝率への影響が微差どころか大差になって表れます。
100%というのは極端な例に思えるかもしれませんが、例えば「タケルライコオーガポンの環境的な立ち位置が非常に良く、全体的な使用率は20%でも決勝トーナメントでは自分以外の7人すべてがタケルライコオーガポンになる可能性が非常に高い」という仮定の下、自分が絶対に予選を抜けられる自信があって優勝確率を最大化するという条件であれば現実的だと言えることもあるかもしれません。

もしシティリーグでクレッフィを採用するなら

また別の視点からこの条件を考えてみます。
クレッフィを採用しない理由は、6試合中5試合以上スタートできる確率が高々25%しかないことが要因の1つでした。
ではもっと確率を上げてみたらどうでしょう。

というわけでクレッフィを複数枚採用したらこんな感じ。

クレッフィ複数採用の場合

先ほどと同様の条件ならクレッフィを3枚採用したら、2回に1回は予選を抜けるという目標までは現実的になりそうですね。
例えばリキキリンパッケージを抜いた枠にクレッフィを採用して3枠を確保する、というのは筆者も考えた構築の1つです。
タケルライコオーガポンが最大多数でないと読むのであればこれは実際良い選択であった可能性があります。
ただ、その場合も、クレッフィでスタートしてかつ早い展開が予想される試合では(2Tにリザードンexやドラパルトexに進化されてしまう等)、対抗するためにこちらも2Tからアクションを起こす必要があり、ドラパルトexの進化＋アカマツを安定させるパッケージ(現物を増やすorテラスタルオーブの採用)や、デヴォリューションの採用などを検討する必要があると感じました。

実際に使った構築

2025 S1使用構築

シャリタツの採用

筆者の構築ではたねポケモンのもう1つの候補であるシャリタツを採用しました。
これはイバラドラパルトというアーキタイプのドラパルトexデッキの側面を高く評価した結果であり、「ぶっちゃけ特性ロックが成功しなくても適切なサポート＋ファントムダイブを言い続ければそれだけのデッキにだいたい勝てるのでは？」という思想の下に成り立っています。
特にこのデッキでは特性ロックが失敗した(またはリキキリンex主体で戦う)展開では、ベンチを絞って大型を押し付けるという戦術を取る場合が多く、その際にドロンチのていさつしれいを使用できる回数が減ってしまうために最終盤でうまくデッキが回らない(≒使いたいサポートを使えない)という場面に一定の確率で遭遇します。
シャリタツはそういった試合を拾ってくれる他、1Tに特性ロックをすることを諦めてでもペパーを探しに行ってエボリューションを打った方が強い展開などで救ってくれる非常に有用なカードです。

スタート率の変化

シャリタツ採用の場合のスタート率

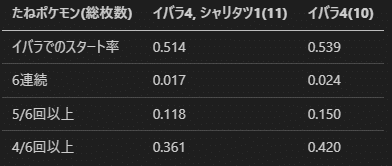
スタート率の単純な比較では2.5%しか変わりません。
例えば5回以上イバラでスタートできる確率を見て、4回出場した場合の期待値がほぼ変わらないという見方もできるかもしれません。
自分の場合はこのあたりの変化量が微差であることから、採用した場合の勝率がどれくらい変動するかで考えました。

例えばシャリタツを採用しない場合の勝率を
・テツノイバラexでスタートした試合の勝率：80%
・それ以外のポケモンでスタートした場合の勝率：40%

シャリタツを採用した場合の勝率を
・テツノイバラexでスタートした試合の勝率：80 + 100x%
・それ以外のポケモンでスタートした場合の勝率：40 + 100y%

と仮定すると、それぞれ勝率は以下のように計算できます

シャリタツを採用していない場合の勝率
= 0.8 * 0.539 + 0.4 * (1 - 0.539) = 0.6156

シャリタツを採用した場合の勝率
= (0.8+x) * 0.514 + (0.4+y) * (1 - 0.514) = 0.6056 + 0.514x + 0.486y

つまり、
0.514x + 0.486y > 0.01
を満たせば、シャリタツを採用した場合の勝率の方が高くなることがわかります。

比較的簡単に思考できる例として、テツノイバラexでスタートできなかったがシャリタツでスタートできた試合(=yのうちの約20%)での勝率の変化を考えます。

初手でペパーもポケギア3.0も引けない確率がだいたい52C8/60C8 ≒ 0.3 
シャリタツがペパーをヒットさせる確率が1-(48C6/52C6) ≒ 0.4
程度ですので、シャリタツのおかげでペパーが引ける確率はおおよそ12%くらいあるということがわかります
これ以降の計算は相当複雑になるのでさらに概算にはなりますが、2Tまでにアカマツを引いていない確率がおそらく40%前後、その場合にシャリタツがアカマツをヒットさせる確率はプレシャスキャリーやエヴォリューションの圧縮を考えると45%程度になりそうで、ポケギア3.0を引いている場合を考慮しても、シャリタツのおかげでアカマツを引き込める確率は10%以上は向上していそうです。
1Tペパー＋2Tアカマツが打てる確率は総合して、0.7*0.7 - 0.6*0.6=13%ほど向上していそうで、最終的な勝率には10%弱ほどの改善が見込めます。

その他にも、ポケギアが初手にあってペパーを外したかつシャリタツがヒットする確率(多分おおよそ1%前後)や、ペパーはヒットしなかったがナンジャモから必要なカードを引けた試合、ボスの指令で時間を稼げた等々の細々した累積で、シャリタツスタートの試合の総合勝率の改善は10%強であると推察できそうです。
条件式に戻してみると、0.2 * 0.486 * 0.1 ≒ 0.01程度の定数項を捻り出せたことになるので、この時点でシャリタツ採用によるスタート率低下のデメリットは帳消しになっていて、シャリタツによる勝率の改善要素が他に存在すれば勝率の改善が正当化できそうです。

例えば最終ターンデッキ20枚のうちの2枚のボスの指令を引ければ勝ちという場面があったとして、シャリタツがこれをヒットさせられる確率は50%ほどあるので10試合に1回でもこのシーンが存在するなら、シャリタツ採用による勝率の向上は5%程度担保できるということになります。

おまけでもう少し一般化してみます。
例えばシャリタツを採用しない場合の勝率を
・テツノイバラexでスタートした試合の勝率：100a%
・それ以外のポケモンでスタートした場合の勝率：100b%
として、計算の都合上0.539≒0.540としてしまうと求める条件式は

(a+x) * 0.514 + (b+y) * (1 - 0.514) > a * 0.540 + b * (1 - 0.540)
0.514x + 0.486y > (0.540a+0.460b) - (0.514a+0.486b)
0.514x + 0.486y > 0.026(a-b)

と、偶然にもかなりきれいなに整理できます。
この式を見るとaとbの差によって超えるべき値が変化することがわかるので、「テツノイバラexでスタートした試合の勝率とそれ以外のポケモンでスタートした場合の勝率の差」が40%を超えない限りは、今回計算したシャリタツによる勝率向上が同様に正当化されそうです。
差が60%(a=90%, b=30%など)とかになったりするようなら、改めて計算してみた方が良いかもしれません。

おわりに

今回は確率から実際にたねポケモンの枚数比を考えた筆者のデッキ構築の工程について解説してみました。
ここまでしっかり文章を読んでいただいたみなさまにはきっと、確率による思考とは正しいものを導いてくれるのではなく、悪いものを省いてくれるものだ、というのが伝わったのではないかと思います。
今回とりあげた2つのうちクレッフィによる勝率向上は一定値を満たしていないから悪いという結論は簡単に出ましたが、シャリタツによる勝率向上は一定値を満たす条件を仮定した上で正当化できる(条件によっては悪くなる可能性もあるし)という結論が関の山です。
簡単に良いとわかる結論を導ける場合も当然ありますが、その場合の多くは確率を計算するまでもなく良いとわかってしまうものです。

でも意外と悪いということは直感ではわかりにくい。
だから計算をすることで悪い方向に進む可能性を潰していくのが重要になるのです。


自分が参加させていただいた一般TCG理論という合本では、今回書いた確率により悪い可能性を潰していくという話をもう少し抽象的な視点から解説しています。

また同様に一般TCG理論の立ち上げ人である茂里さんは、とある記事で自分の主張とほぼ同様の次のような主張をされています。

数字は良いことを良いとはあまり示してくれないが、よく悪いことを悪いと示してくれる。そしてその悪さを測る指標にもなるのだ。そこからどうすれば良くなるかのアイデアが生まれるものである。

https://note.com/maddogmtg/n/nade82044f352

カードゲームを論理的に考えるという過程で数字は避けて通れないツールです。
そして正しく条件を計算しようと思えば思うほど計算を複雑になって忌避したくなってしまうものです。
だから正しく計算するのをやめましょう。
概算で良い。状況を簡単にして良い。そうして簡単なパターンから求めたい状況を抑え込むイメージで、その考え方が悪くないことを証明するツールとして使えば良いのです。

一般TCG理論では直感を補強するツールとしての論理を非常に大切にしています。
もしカードゲームに対して論理的であるという感覚が思っていたのと違ったというのであれば、ぜひ我々の考え方に触れていただきたいと思います。

宣伝もこのあたりでそれでは

明日はパルキア中野さんの
「PCGシリーズ、およびSVシリーズにおける逆転要素について」
です
お楽しみに！

いいなと思ったら応援しよう！