
【建築構造】判別式を使えるようになろう!
こんばんは、ひろです!
前回の記事では、構造物の種類とその特徴を紹介して、最後に構造物の種類を判断する方法として判別式を紹介しました。
今回は、例題を交えながら判別式の使い方を説明していきたいと思います!
この記事の内容は、こちらのブログでより詳しく解説しています!
もっと詳しく学びたい方は、下のURLをクリックしてください。
判別式のおさらい
前回、構造物の種類を見分ける方法として次の判別式を紹介しました

判別したい構造物に対して判別式を使って不静定次数 m を求めます。
m < 0 のとき不安定構造物、m = 0 のとき静定構造物、m > 0 のとき不静定構造物と判断することができました。
ここからは、この式についてもう少し細かく説明していきたいと思います!
反力の数え方!!
反力の数は支点の種類によって異なります。
各支点における反力の数は次のようになります!

剛節接合部材数の数え方!!
剛節接合部材数は接合部の形状によって異なります。
各接合部における剛節接合部材数の数え方は次のようになります!

例題①
実際に、例題を通して判別式を使ってみましょう!

まずは、単純梁の問題です!
実際に手を動かして、静定構造物であることを確認してみましょう!
例題②

つづいて、上記のラーメン構造に関して考えてみましょう!
まずは、答えを見ずに自分の力で解いてみましょう。
例題③

最後に、トラス構造の問題です!
例題はこれで終わりです!
解答&解説
ここからは、例題の解説を進めていきます!
まずは、例題①から解説していきます!
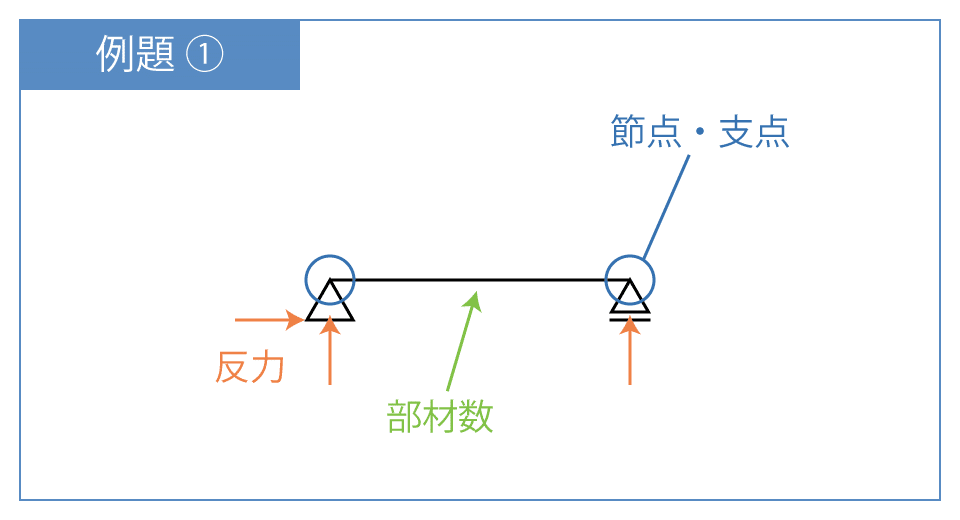
判別式で不静定次数を求め、構造物の種類を判断していきましょう!
不静定次数を求めるのに必要な値を考えてみます。
反力数は3つなので、n = 3
部材数は1つなので、s = 1
剛節接合部はないので、r = 0
節点・支点数は2つなので、k = 2
よって 、m = 3 + 1 + 0 - 2×2 = 0
単純梁は静定構造物であることが確認できました!
次に例題②の構造物について確認していきましょう。

不静定次数を求めるのに必要な値を考えてみます。
反力数は4つなので、n = 4
部材数は3つなので、s = 3
剛節接合部材数は剛節数1の接合部が2つあるので、r = 2
節点・支点数は4つなので、k = 4
よって 、m = 4 + 3 + 2 - 2×4 = 1
したがって不静定構造物となります。
つづいて、例題③の構造物について確認していきましょう。

不静定次数を求めるのに必要な値を考えてみます。
反力数は3つなので、n = 3
部材数は6つなので、s = 6
剛節接合部はないので、r = 0
節点・支点数は5つなので、k = 5
よって 、m = 3 + 6 + 0 - 2×5 = -1
したがって不安定構造物となります。
ここまで、解答&解説をみて、どうでしたか?
できた!という人もいれば、難しかった…という人もいるでしょう。
でも大丈夫!今できなくても、これから解けるようになればいいんです!
判別式が使えない例
前回の記事でも触れましたが判別式が使えない場合もあります!
最後に判別式が使えない例を紹介します!

この梁について判別式で不静定次数を求めます。

これまでの例題と同様に、不静定次数を求めるのに必要な値を考えて不静定次数を求めてみると
反力数は5つなので、n = 5
部材数は4つなので、s = 4
剛節接合部はないので、r = 0
節点・支点数は5つなので、k = 5
よって 、m = 5 + 4 + 0 - 2×5 = -1
不静定次数は0より小さくなり、判別式では不安定構造物と判断されます。
しかし、力のつり合い条件式の数を考えてみると、ΣH=0, ΣV=0,ΣM=0の3式に加えて、2つのヒンジ部でそれぞれつり合い式が立てられるため合計で5つの式を立てることができ、これは反力数と一致します。
つまり、判別式の結果では不安定構造物でしたが、本当は静定構造物だということです!
また、今回の例とは逆に判別式の結果では静定構造物と判断されたが、本当は不静定構造物という場合もあります。
さいごに
今回は、判別式の使い方について解説していきました。
構造物の種類を把握することは反力・応力を求める上でとても重要です。
そのためにも判別式の使い方をマスターしましょう。
例題を通して判別式の使い方が分かってもらえたら嬉しいです!
また、判別式が使えない例も紹介しました。
判別式が万能ではないということを頭の片隅に置いといてください!
基本は反力数と力のつり合い条件式の数で判断し、判別式はあくまでも補助的なものです。
構造物の種類の判断はまた別の機会にも例題を通して解説しようかと思っています。
このnoteでは、建築・建築学生の生活についてなるべくわかりやすい情報を提供していきます!
こんな内容について、書いてほしいといった要望があったらぜひコメントお願いします。
ではまた
いいなと思ったら応援しよう!

