
帰納と驚き 第1章 帰納
私たちは日々さまざまな推論に基づいて生活している。
空がどんよりと曇れば雨降りを心配してカサを求め、
青信号が点滅すれば赤に変わることを予期して足を速め、
舞い落ちる紅葉にやがて訪れる冬を予感する。
それらの推論のすべてが帰納推論と呼ばれるものだ。
帰納推論は過去の個別事例(たとえばA、B、Cなど)を前提として同様の全事例(たとえばA、B、C、D…、Z)にあてはまる一般法則を導く推論方法であり、ご覧のとおり前提(A、B、C)よりも帰結(A、B、C、D…、Z)のほうが情報量が多いため、情報量の増加を伴う推論だと言われている。
本章ではまず、この情報量の増加の前段階に情報量の減少過程が隠れていることを明らかにする。
次いで、私たちの有するすべての知識および認識がこの情報量の減少過程を経て獲得されていることを指摘し、以上を受けてこの情報量の減少過程を広義の「帰納」と定義する。
この「帰納」という概念は本稿において最も重要な概念であり、私たちは次章以降、この帰納という概念をもとに世界と私の成り立ちを紐解いていくことになる。
演繹推論と帰納推論
まずは帰納推論を含む推論一般について簡単に整理しよう。
私たちの行う推論は、演繹推論と帰納推論に大別される。
演繹推論とは、一般的な前提から個別の結論を導き出す推論方法であり、例えば「すべてのスワンは白い」という前提から「スワンAは白い」「スワンBは白い」「スワンCは白い」などの結論を導き出すことだ。
「すべてのスワン」にはあらかじめスワンA、スワンB、スワンCが含まれているので、結論の内容は前提内にすべて含まれていることになる。
このため演繹推論は前提が正しければ、結論も必ず正しく、またその推論の前後で情報量が増えることもない。
一方、帰納推論とは、個別の事例から一般的な法則を導き出す推論方法であり、上記の例に倣えば「スワンAは白い」「スワンBは白い」「スワンCは白い」という個別事例から「すべてのスワンは白い」という一般的な結論を導き出すことだ。
結論の「すべてのスワンは白い」には「スワンDは白い」「スワンEは白い」「スワンFは……」など前提にない情報が含まれているため、推論によって情報量は増加している。帰納推論が情報量の増加を伴う推論方法だと言われているのはこのためだ。
また前提が正しかったとしても結論は必ずしも正しいとは限らない。スワンPあたりは紫色をしているかもしれない。
上記のように演繹推論は情報量を増やさないため、そこで行われているのは前提条件のなかに埋もれている知識の発掘であって、新しい知識の獲得ではない。演繹推論の結論は、明示されていなかっただけで実は既に知られていた内容にすぎないのだ。
「テーブルの上にコップがある」などの事実認識を除いて、こと世界の法則に関してはいえば、私たちが世界から新しい知識を獲得するためには帰納推論による以外に方法がない。
演繹推論の前提となる一般法則もまた、過去に帰納推論によって得られたものであることを考え合わせれば、私たちの法則的知識はすべて帰納推論によって得られたものだということになる。
帰納推論
では、すべての法則の源泉ともいえる帰納推論とはどのような推論なのだろう?
上記の例を図で示してみよう。
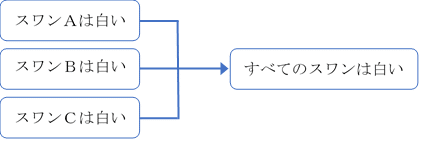
スワンA、B、Cという個別事例から、すべてのスワンに関する一般的な結論が導かれている。
ここで注目したいのは、結論「すべてのスワンは白い」には前提「スワンA、B、Cは白い」が含まれてはいるが、この結論のみから、この結論がどのスワンをもとに導かれたのかを知ることはできない、という点だ。
なぜだろう?
それは、結論のなかにスワンA、B、Cを特定する情報が含まれていないから、言い換えれば、個別性に関する情報が推論の過程で消去されているからに他ならない。
このことを明示的に上記の図を書き直してみよう。
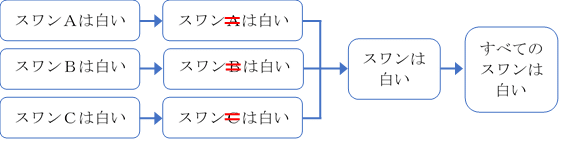
推論の前段階で前提間に存在していたA、B、Cという差異が消去されて、残った共通部分が結論として導かれている。
結論を揃えるため最後に「すべてのスワンは白い」を書き加えたが、これは「スワンは白い」と同義であるため不要だ。

また、前提は複数でなくてもかまわない。

いずれの場合も、前提に含まれていた個別情報が消去されることで、結果として文の内容が一般化していることがわかる。
情報量の減少(個別情報の消去)が、情報量の増加(文内容の一般化)を引き起こしているわけだが、この因果関係に示されているとおり、本質は情報量の減少にあり、情報量の増加は言うなればその結果にすぎない。
ここでいう減少している情報量とは見てのとおり、文中に記された語あるいは意味であり、増加している情報量とはその文によって指し示される個別具体的な事例の数または範囲だ。
硬い言葉を使えば、「文の内包が減少することで、文の外延が増加している」ということになる。
知識獲得における情報量の減少過程
さて、ここまで帰納推論に隠されていた情報量の減少過程について述べてきたが、この過程はなにも帰納推論に限ったものではない。
法則的知識に限らず、私たちの有する知識や認識のすべてはこの情報量の減少によって獲得されている。
そのことを個物の認識、具体概念の獲得、抽象概念の獲得の三つに分けて以下に示そう。
・個物の認識

ここに三つの図を示した。
とてもシンプルな絵だが、できれば実際に私たちが目にした景色だと思ってほしい。
ひとつめは青い中に黄色がある景色、
ふたつめは赤い中に黄色がある景色、
みっつめは黒い中に黄色がある景色だ。
この三つの景色から、青、赤、黒の部分を個別情報として消去し、共通項である黄色を抽出することで、私たちは黄色を一つの個物として認識することができる。
そして、そのように個物を認識するとき、そこではもう一つの情報量の減少が起きている。そのことを示すために、上記三つの景色のそれぞれの時間を明らかにしよう。
ひとつめは正午の景色、
ふたつめは夕方の景色、
みっつめは夜の景色だ。
この三つの景色から、正午、夕方、夜といったそれぞれの時刻を個別情報として消去することで、無時間的あるいは通時的な黄色い物体の存在が共通項として抽出される。
このように、私たちは対象の存在を認識するときは常に、その時々の瞬間的な認識から、ただ端に「ある」といえるような無時間的あるいは通時的認識を獲得してもいるのだ。
・具体概念の獲得
ヌッペラを知らない私に、誰かがヌッペラとは何かを教えてくれるところを想像してみよう。
その人は、「これがヌッペラだ」と言って、私の前に見たことのない物体を三度提示してくれる。
ひとつめは、黄色くて丸くて、棘がついている物体。
ふたつめは、黄色くて丸くて、深いしわが刻まれている物体。
みっつめは、黄色くて丸くて、小さな穴が開いている物体。
そして、その三つの物体から、私は「なるほど、ヌッペラとは黄色くて丸い物体のことなんだ」というふうにヌッペラの概念を理解する。
もう説明する必要はないかもしれないが、ここにおいても、棘、しわ、穴の個別情報が消去されて、三つの物体の共通項が概念として残るという、帰納推論で見てきたものとまったく同じ過程が現れている。
・抽象概念の獲得(数を例に)
上であげたヌッペラのように、ある対象一般を指す具体概念を使用すると、複数の対象を一括りにまとめて把握することが可能になる。
「りんごAとりんごBがある」を「二つのりんごがある」と認識する場合などがそれにあたる。
その「二つのりんご」、「二つのコップ」、「二匹のネコ」などの具体事例から、りんご、コップ、ネコを個別情報として消去し、後に残る共通項を抽出することで獲得されるのが2という数だ。
「白い」などの性質や「前/後」などの関係性を表す抽象概念もこの数と同じように、具体概念に基づいた現実認識から具体概念そのものを個別情報として消去することによって獲得することができる。
私たちは背景を個別情報として消去することで、目に映る世界から対象を分節し、時刻を個別情報として消去することで、対象を客観的世界のなかに固定し、さらにその固定された対象間の差異を個別情報として消去することで具体概念を獲得し、その具体概念自体を個別情報として消去することで抽象概念を獲得している。
そして、それら具体概念と抽象概念とを用いた現実描写を前提として、そこから個別情報を消去することで様々な一般法則を導き出しているのだ。
以上見てきたように、知識獲得の過程はすべて個別情報が消去される過程であり、すなわち情報量の減少過程であった。
本稿では、世界と私を語るにあたって決して看過することのできないこの情報量の減少過程を広義の「帰納」と定め、これよりこの「帰納」が世界と私の成り立ちにどのように関わっているかを検討していくことにしたい。
個別情報と共通項
さて、ここまで情報量の減少過程を描写するにあたって「個別情報」「共通項」という言葉を使ってきたが、何が個別情報で何が共通項なのかは決して自明なことではない。
その二つは恣意的に、あるいは偶然的に線引きされているのだ。
以下にその例を示してみよう。
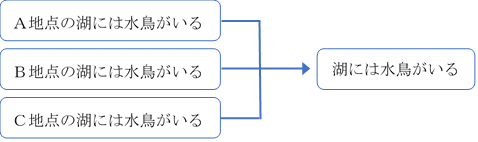
この帰納推論ではA地点、B地点、C地点という位置情報が個別情報として消去され、「湖には水鳥がいる」という結論が導かれている。
ではこの位置情報をより具体的にしてみよう。

前提間の差異を個別情報として消去すると、「日本の湖には水鳥がいる」という結論が帰納される。
では、こう書いてみるとどうだろうか。

今度は「日本東北地方の湖には水鳥がいる」と帰納することが正しいように見えるだろう。
逆に言えば、
日本東北地方秋田県の田沢湖には水鳥がいる、
日本東北地方青森県の十和田湖には水鳥がいる、
日本東北地方福島県の猪苗代湖には水鳥がいる、
の三つの前提は、位置情報全体を個別情報とみなすこともできるし、「東北地方〇〇県」を個別情報とすることもできれば、「〇〇県」だけを個別情報とすることもできるということだ。
帰納に伴って個別情報の消失が起きると言っても、どの範囲を個別情報とみなすかは恣意的にならざるをえない。
また、上記のように前提が複数ある場合は、個別情報と共通項の線引きはある程度限定されているといえるが、前提がひとつの場合はその境界線はどこにでも引くことができる。
私たちはここまで、帰納とは前提の個別情報が消去され共通項が残ることだと考えてきた。
しかし、個別情報と共通項の線引きがあらかじめ決まっていないのであれば、同じことではあるが次のように言ったほうがより正確だろう。
すなわち、帰納とは前提を消える要素と残る要素に二分することである、と。
私たちはそのうちの消える要素を個別情報、残る要素を共通項と呼んでいるのだ。
帰納の妥当性
前節では個別情報と共通項の線引きが恣意的になされていることを示したが、この二者の線引きは帰納された帰結の妥当性にも影響を与えることになる。
ではどのように影響するのか、
「太陽系地球日本東北地方秋田県の田沢湖には水鳥がいる」
という前提から帰納推論によって導かれる以下の六つの結論を例に考えてみよう。
(1) 太陽系地球日本東北地方秋田県の田沢湖には水鳥がいる
(2) 太陽系地球日本東北地方秋田県の湖には水鳥がいる
(3) 太陽系地球日本東北地方の湖には水鳥がいる
(4) 太陽系地球日本の湖には水鳥がいる
(5) 太陽系地球の湖には水鳥がいる
(6) 太陽系の湖には水鳥がいる
結論(1)は前提から減少する情報量がゼロの結論だから、前提が正しければ必ず正しい。
そして(2)以降は減少する情報量が次第に大きくなっており、それにしたがって結論の確からしさがだんだんと怪しくなっていくのが見てとれる。
田沢湖に水鳥がいるなら同じ秋田県内の湖にも水鳥がいると推論しても問題はないだろう。
東北地方に関しても妥当と言えそうだ。
しかし、日本全域となると少し不安になる。
それだけ広くなると何らかの原因で水鳥が寄り付かない湖があってもおかしくないように思える。
(5)の地球全域の湖となると、もう間違っている確率のほうがずっと高い。
地球上に水鳥のいない湖が一つもないなんてことがあるだろうか?
それが太陽系全体まで広がるともう絶望的だ。
地球を除く太陽系の惑星に湖と呼べる地形があるかどうか私は知らないが、仮にあったとしたら、そこには絶対水鳥はいないだろう。
このように同じ前提から帰納推論をおこなう場合、情報量の減少が小さいほどその結論の妥当性は担保され、情報量の減少が大きくなれなるほどその妥当性もやはり失われていく。
以上のことは帰納推論だけでなく帰納一般にも当てはまる。
世界を帰納的に把握するに際して、失われる情報量が大きければ大きいほど、獲得した知識は世界そのものから乖離してしまうことになる。
また、どれだけ情報量の減少を小さく抑えても、私たちが世界を帰納的に把握するかぎり、そこには必ず情報量の減少があって、その分だけやはり知識の妥当性は失われることになる。
真に正しいと言えるのは、すべての帰納の前提となる世界そのもの、ただそれだけなのだ。
まとめ
・帰納推論とは前提から情報量の減少過程を経て一般法則を導く推論である。
・すべての知識および認識は情報量の減少過程を経て獲得される。
・本稿ではこの情報量の減少過程を広義の「帰納」と定義する。
・帰納によって前提は消える要素と残る要素に二分される。
・真に正しいのはすべての帰納の前提となる世界そのもののみである。
