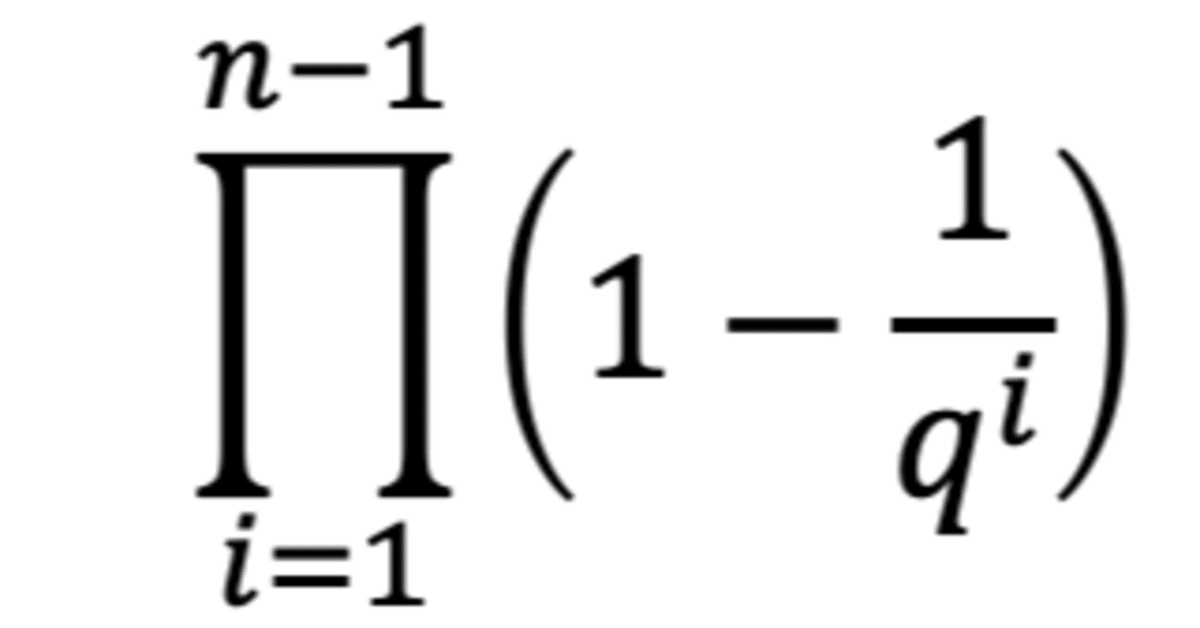
有限体上の正方行列が正則になる確率

UOVの署名生成において, 表記の問題が現れます. ここではこの問題について考えてみましょう. つまり, 以下の問題を考えます:

問題

有限体$${\mathbb{F}_q}$$上の$${n}$$次正方行列が正則になる確率は,

$$
 \prod_{i=1}^{n-1} \left( 1-\frac{1}{q^i} \right)
$$

である. これを示せ.

解答

正方行列が正則であるとは, 各列ベクトルが一次独立であることに必要十分である. $${a_i}$$ を $${\mathbb{F}_q}$$ 上のベクトルとすると, 
($${a_1}$$と$${a_2}$$が一次独立となる確率) $${= 1 - \frac{q}{q^n}}$$.
($${\because}$$  $${a_2}$$としてとりうるベクトルが$${q^n}$$個あり, そのうち$${a_1}$$に従属なベクトル$${ca_1}$$が$${q}$$個あるので, 余事象の確率よりしたがう)
同様に, 
($${a_1}$$と$${a_2}$$と$${a_3}$$が一次独立となる確率) $${= (1 - \frac{1}{q^{n - 1}})(1 - \frac{q^2}{q^n})}$$.
($${\because}$$  $${a_1}$$と$${a_2}$$が一次独立かつ, $${a_3}$$としてとりうるベクトルが$${q^n}$$個あり, そのうち$${a_1, a_2}$$に従属なベクトル$${c_1a_1 + c_2a_2}$$が$${q^2}$$個)
$${\vdots}$$
($${a_1, \cdots, a_n}$$が一次独立となる確率) $${=  \prod_{i=1}^{n-1} \left( 1-\frac{1}{q^i} \right)}$$.