
PRML:1.2節(確率論)の紹介(PART3)
クリスマスシーズンであったため、最近はアドベントカレンダー関連の記事がたくさん投稿されました。私も1つは記事を投稿しようということで、PRMLゼミ資料を整理したものをアップします。
本ノートでは、1.2節の発表資料の一部(1.2.4節)をアップし、コメントを記します。資料はできるだけ原著に忠実に作成することを心がけていますが、本noteは、原著だけでなく、自分自身が感じていることも含めてまとめています。
↓ 1.2.4節関連の内容をまとめたスライドはこちらです。
↓ 1.2節に関する過去の記事はこちらです。
正規分布(ガウス分布)
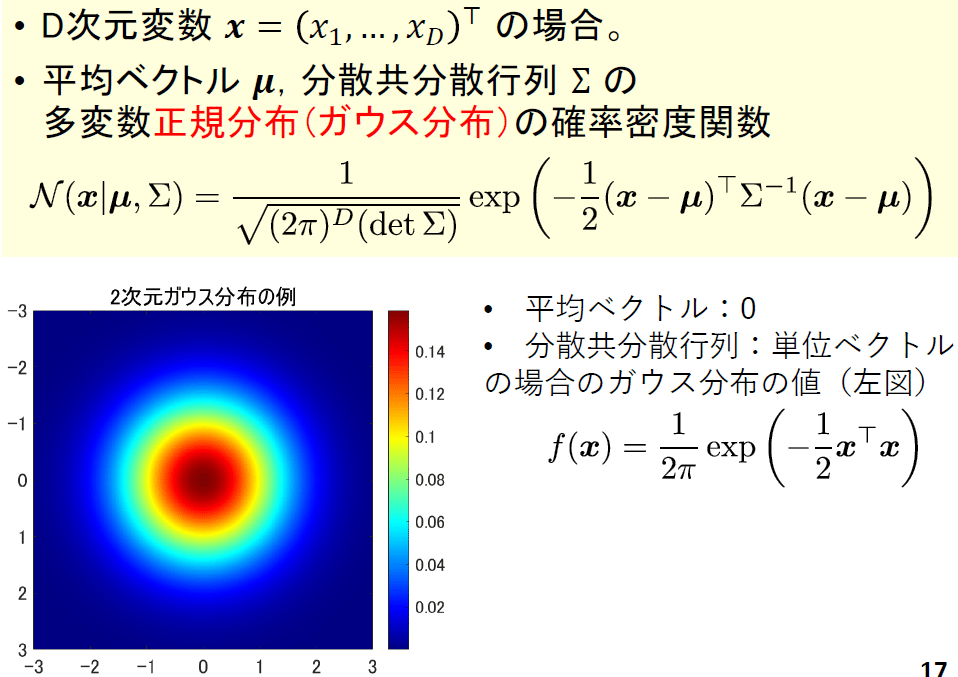
1.2.4節ではガウス分布の基礎を扱います。ガウス分布の確率密度関数と形状は以下の通りです。これは確実に覚えないといけない式とグラフです。

実際に扱うデータは多変量であるため、多変量のガウス分布も重要です。多変量の場合は以下の通りです。こちらも確実に覚えることが必要です。
※ちなみにここで考えているのは実数データですが、複素数データを扱う場合は係数が別物になるそうです。大学院の授業で音のアレイ信号処理について習った際は複素ガウス分布について扱っていました。
観測データからガウス分布のパラメータを推定する:最尤推定
1.2.4節の話の後半は、観測データからガウス分布のパラメータを推定する方法が記されています。ここでは最尤推定によりガウス分布の平均と分散を推定していました。その話に入る前に、各観測データがあるガウス分布から独立に生成されている「独立同一分布」の話がありました。
その後に最尤推定でパラメータを推定する方法が記されています。推定方法も重要ですが、関連する話も重要です。ゼミでは関連する話題と合わせながら、理解を深めていきました。
「最尤推定」は観測されたデータ集合の同時確率を最大にするパラメータを「最も尤もらしい(もっとももっともらしい)」と考える方法です。同時確率密度関数をパラメータの関数とみたものは「尤度関数」と呼ばれます。多くの場合、尤度関数の対数、対数尤度関数が解析にとって有用です。

最尤推定の解
対数尤度関数の最大化により、パラメータの推定値を得ることができます。その結果として、観測データの平均と分散が、ガウス分布のパラメータの最尤推定量となることがわかります。

不偏推定量
最尤推定量は観測データから得られる量であり、決まった値ではありません。そのため、その最尤推定量が真の値と近いかどうかは確認するべきことです。そこで、最尤推定量の期待値を考えます。
推定量の期待値が真の値と一致するとき、その推定量は「不偏推定量」であるといいます。推定値が不偏推定量であると、推定値は真値の周りに分布しているといえるので、不偏推定量は良い推定量の1つといえます。
平均値の推定量については簡単な計算で不偏推定量であることが確認できます。

分散の最尤推定量は不偏推定量ではない
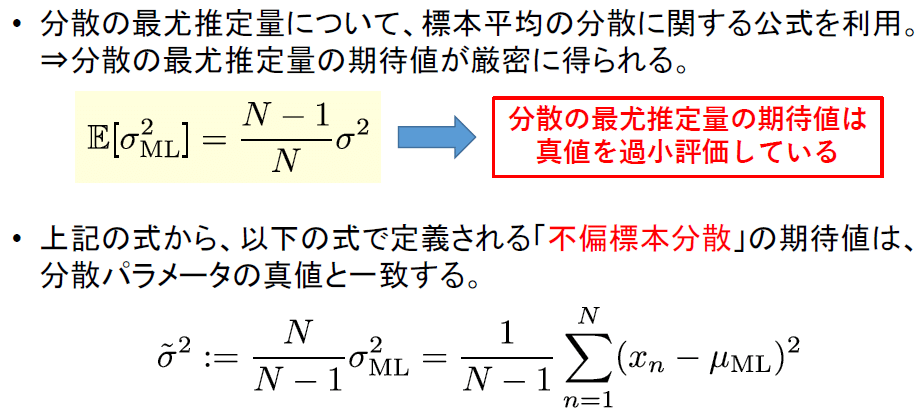
分散の最尤推定量は少々面倒ではありますが、不偏推定量ではないことが確認できます。そして、その計算の過程から、分散の最尤推定量は真値を過小評価しているということがいえます。

計算の過程から、平均との差の2乗の総和をデータ総数Nではなく、N-1で割ったもの(不偏標本分散)の期待値が分散パラメータの真値と一致することが確認できます。そのため、N-1で割ったものは「不偏標本分散」と呼ばれます。
※本資料はGithubにもアップロードしています。本ノートおよびアップロードしている資料について何かありましたら、noteのコメント欄までお願いします。
