
PRML:1.1節(多項式曲線フィッティング)の紹介(PART2)
『パターン認識と機械学習(上)』というあの黄色本を用いてゼミを行った際の発表資料をnoteにもアップすることにしました。noteにはゼミ資料を再編集したものをアップします。本ノートでは、1.1節の部分の発表資料をアップし、その後半部分のコメントを記します。
↓ 1.1節の説明資料はこちら。
↓ 上記資料前半部分のコメントはこちらにまとめてあります。
1.1節の前半では多項式曲線フィッティングの最も単純な方法を示し、データ数が少ないと過学習が生じるという課題があることを紹介しました。後半部分では、過学習の解決方法の一例を示します。
汎化能力の評価
過学習の解決方法を示す前に、汎化能力の評価指標を示します。
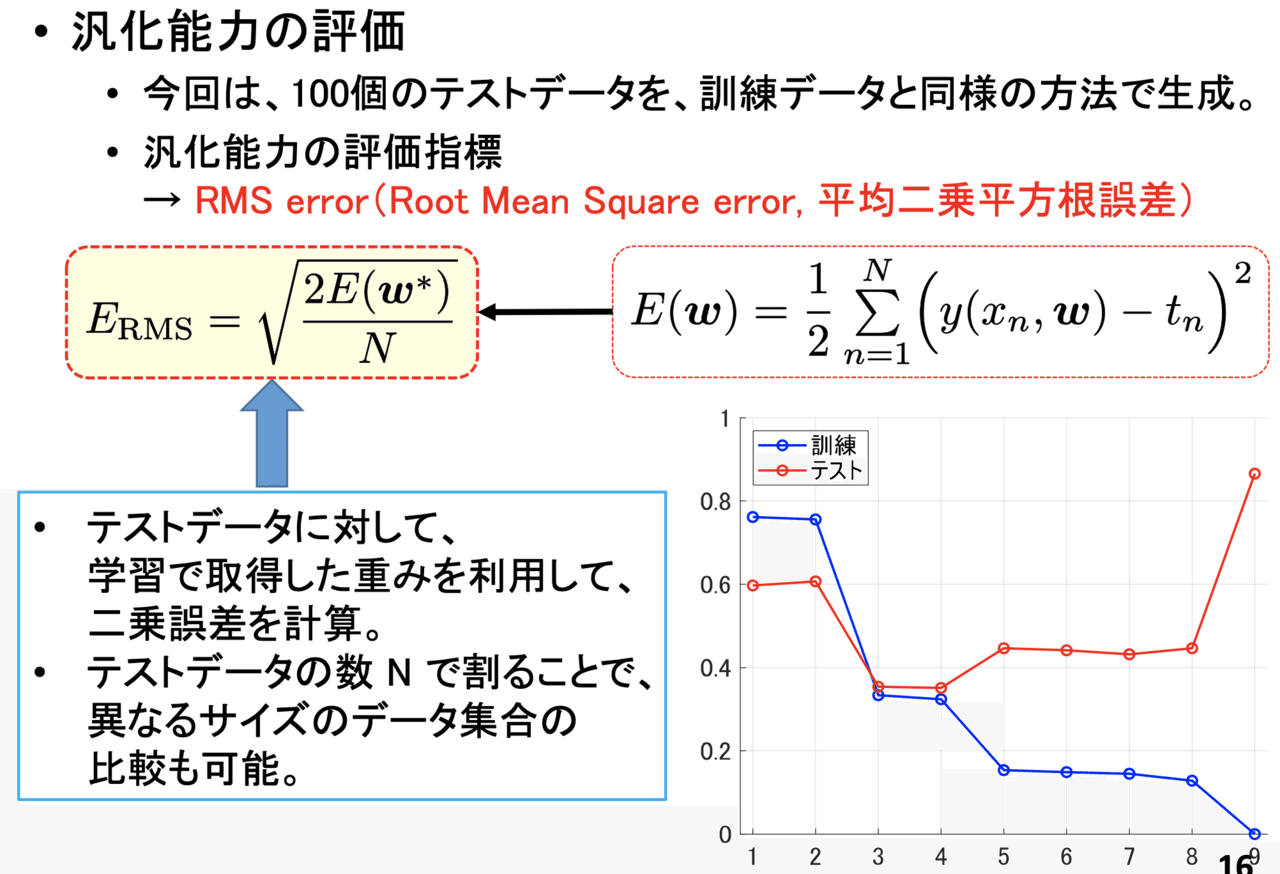
学習により取得した重みが有用かどうかを評価するには、訓練データと同じ方法で取得したテストデータ(validation data、検証用データの方が適切?)から、RMSを計算するという方法があります。RMSを利用することで、モデルの次数 M がどのような値の時に過学習が起きているかを定量的に把握することができます。
私が用意したデータに対して計算すると、M = 3, 4 の場合にテストデータ(検証用データの方が適切?)のRMSが最小となることが確認されました。このようなことから、自分が設定した E(w) の下では、3次あるいは4次のモデルが一番良いことがわかります。
※このスライドに示した通り、用意したデータ数 N で割ることで、用意したデータ数によらず比較することができます。
訓練データ数を増やす
過学習を回避する1つの方法に「訓練データ数を増やす」ということがあります。これは最もシンプルな過学習の回避方法ですが、現実には訓練データ数を増やすことが厳しい場合が多いです。

※ここで紹介している多項式曲線フィッティングとは異なりますが、深層学習による画像処理では、画像に適当なノイズを加えたもの、左右や上下を反転させたものを用意するなどして仮想的に訓練データ数を増やすことがあります。
※自分で大量のデータを用意することは容易ではありません。そのような場合は世界中の研究者が公開しているデータセットが役に立ちます。大学院の講義で先生がデータセットがまとめられているWebサイトを紹介していました。どのようなデータセットがあるか興味のある方は「機械学習 データセット」などのキーワードで調べてみてください。
重みパラメータ w の値に注目する 〜正則化の意味〜
過学習を回避する方法として一番よく使われているのが「正則化」です。
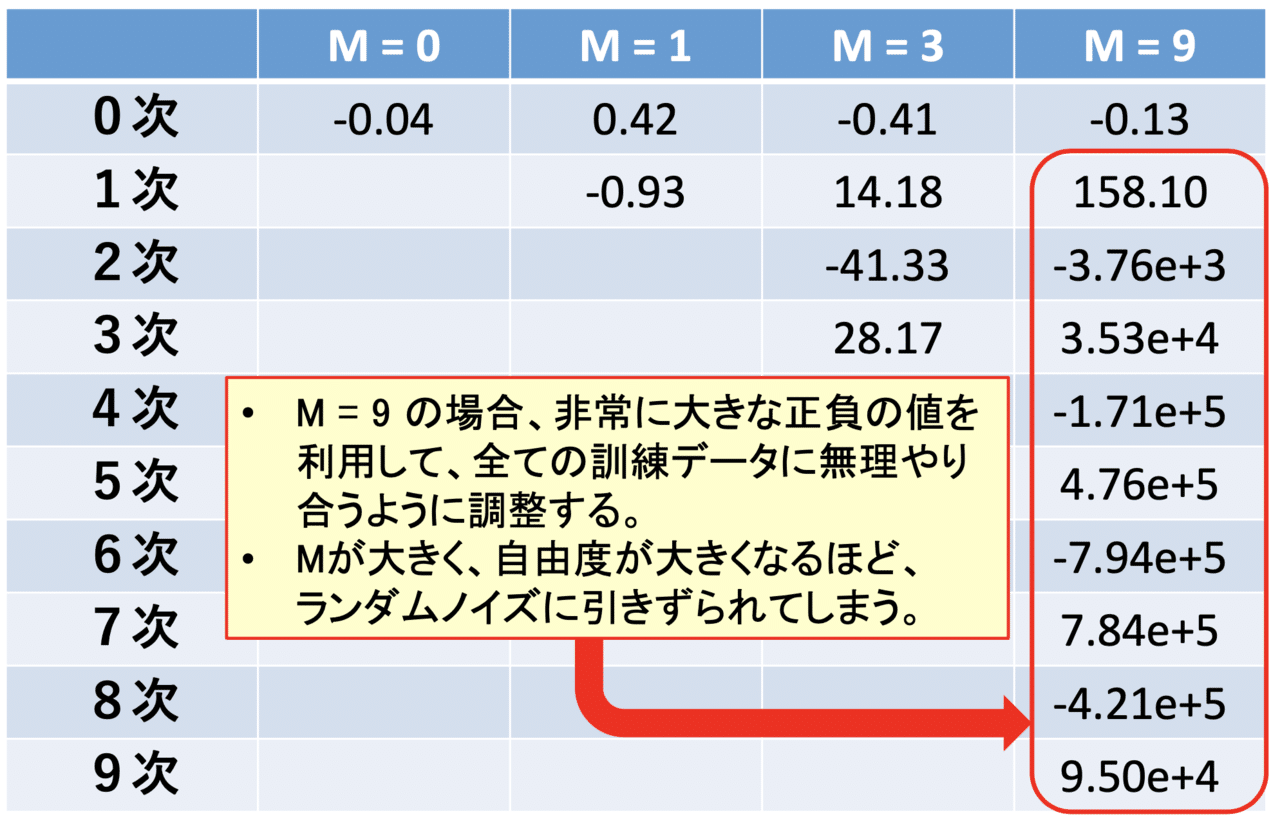
正則化の話に入る前に、過学習が起きる場合の重みパラメータ w の値に注目してみます。今回は訓練データが10個ということもあり、9次関数で近似しようとすると、非常に大きな正負の値を利用することで、無理やり全部の訓練データに合わせようとしています。このようなことが起きてしまうと、ノイズに対して脆弱になってしまいます。
正則化の定式化
上記のことから、重みパラメータの大きさを適度に抑制すると、過学習を回避できるかもしれないと考えられます。このことを定式化すると、下のスライドのようになります。
今まで見てきた二乗誤差に、重みパラメータ w のノルムの2乗を付け加えたものを目的関数に設定して、これを最小にする w を最適な w とします。こうすることで、重みパラメータも適度に小さくしなければならず、重みパラメータの大きさを抑制することができます。

※具体的にどのようにすれば、重みパラメータ w を計算できるかは上記PDFの15枚目(22とページ番号が振られているスライド)を参照してください。
正則化により重みパラメータを計算した結果
正則化項を加えた目的関数を最小にする w を使って、真の曲線の近似曲線をプロットすると、以下のようになります。ここでは正則化がないと過学習が起きてしまう9次関数で近似しました。
正則化項を加えるだけで、過学習が発生していないことが確認されます。近似の程度は正則化パラメータの値によって異なり、正則化パラメータが大きすぎると、重みが0に近づいてしまい、逆に真の曲線の近似として不適切な状態になってしまいます。正則化パラメータの選択については慎重に検討する必要があります。

※本資料はGithubにもアップロードしています。本ノートおよびアップロードしている資料について何かありましたら、noteのコメント欄までお願いします。
