
【Minecraft解析】燃費の良いエリトラの飛ばし方
1. 目的
本記事ではMinecraftの飛行アイテムである「エリトラ(Elytra)」の挙動解析結果に基づいて、「燃費が良い」(=ロケット花火の消費が少ない)という条件に注目し、最適な飛ばし方を求めた結果を解説します。
ここでは既存の動力飛行→滑空の2段階の解析にとどまらず、動力飛行→エネルギー回生→滑空の3段階飛行を提案し、2段階飛行の改善を試みます。
2. 背景
エリトラの飛行挙動は現実世界の滑空機やムササビスーツなどを模したプログラムが組まれています。(あくまでも感触を模しているだけであって原理上は全く違います)
このプログラムは前Tick(マイクラにおける計算頻度で、描写のフレームと似た概念。1秒に20回)から3方向速度・位置とカーソル角度(ピッチ・方位)を引数とし、現在Tickの3方向速度・位置を出力します。
エリトラ単体では空気抵抗で運動エネルギーが消費される現象がおおむね再現されているため、(おおざっぱではあるが)ピッチを上げて運動エネルギーを位置エネルギーに交換した分程度しか上昇できません。エリトラで高度をあげるためには、ロケット花火(Fireworks)を使うことが必要となっています。
そのため、繰り返しですが、本記事ではあくまでも「燃費が良い」(=ロケット花火の消費が少ない)条件(飛距離に比例)に特に注目し、最適な飛ばし方を求めます。
(追記:これとは別に「耐久値効率」(=耐久値の消費が少ない)の概念もあります。こちらは上記とは対照的に飛行速度(耐久値は時間に比例して減少していくため)に比例します。比較するために少しだけ触れます)
3. 計算方法
本記事に掲載した結果は全てMinecraft上で実際に飛ばして計測したものではありません。これは、飛行時・計測時に発生する誤差を避けるためでもありますが、時間と手間を大幅に節約するためというのが主な目的です。具体例を出すと、次項に解説する定常状態飛行においても179通りのフライトを一本ずつ1000tick(ラグ無しで50秒)行うことが必要で、暇人かラボ畜でもない限りとてもできません。
代わりに、マイクラのソースコードを再現したものをScilabというほぼ無料版Matlab上で実行する方法を取りました。
滑空用の再現コードはここにあります。
https://gist.github.com/samsartor/a7ec457aca23a7f3f120
(なお、Snapshot 15w42a以降では以下のような変更があります。)
line 55:
this.velY += yacc * 3.2; //Used to be 3.5ロケット花火使用時は飛行挙動が別のものに切り替わります。こちらに関してはネット上で見つからなかったので、IntelliJを用いて、自力でソースコードを読み取って再現したものがこちらになります。(1.19.2でも確認)
計算を容易にするため、以下のdurationは{Flight:1}のときの中央値を取り、25[tick]とします。シミュレーション時間と結果の解像度の兼ね合いで、ピッチ角1度刻みでシミュレーションを行います。
duration = (10*(1+Fireworks.Flight)) + rand.nextInt(6) + rand.nextInt(7);
v(1) = v(1) + pitchcos*0.1 + (pitchcos*1.5 - v(1)) * 0.5;
v(2) = v(2) - pitchsin*0.1 + (-pitchsin*1.5 - v(2)) * 0.5;
x(1)=x(1)+v(1);
x(2)=x(2)+v(2);このプログラムからわかるように、ロケット花火使用時の速度はどこを向いても一定になっています。(挙動としては終端速度に漸近しているような感じですが、いかんせん終端速度に達するまでが早い(時定数が小さい))
なお、垂直の飛行プロファイルに注目するため、水平方向の座標を1軸のみに限定します。(xとyに対してのみの計算)
4. 結果・考察
注意:Minecraftでは上向きの角度が負(-)の値、下向きの角度が正(+)の値となっています!
4.1 定常滑空飛行
ここでは初期条件の速度$${\overrightharpoon{v}=0}$$、位置 $${\overrightharpoon{x}=0}$$ からシミュレーションを開始し、tick=1000となったところで終了し、速度と位置を記録します。
記録した速度と位置を以下の図1で示します。ここでGlide Ratio(滑空比)は速度の水平成分と鉛直成分の比率 $${r = v_x / v_y}$$ であり、滑空比が大きければ大きいほど、同じ下降の分で飛行できる距離が遠くなります。このため、滑空比が大きいほどロケット花火の消費が少なくなり、「燃費が良い」状態と言えます。

図からわかるように、滑空比は $${\phi=0\degree}$$ で最大値 $${G=11.2 : 1}$$ を取っており、その近傍を見ると、正の値側(マイクラでは下向き)では緩やかに降下するのに対し、負の値側(マイクラでは上向き)では急降下することがわかります。
最大値 $${\phi=0\degree}$$ で飛行することがもっとも「燃費の良い」状態ですが、ずれて負の値側に入ることを回避するために、少しだけピッチダウン(2~5°)が現実的です。
一方で、水平速度 $${v_x}$$ に注目すれば、$${\phi=55\degree}$$ 付近の最大値では滑空比が4:1程度しかありません。そのため $${0\degree≤\phi≤55\degree}$$ の間では燃費(飛距離)対飛行速度(耐久値効率)のトレードオフだと考えられます。
この結果は以下のサイトにも非常によく一致しています。
4.2 動力飛行(2段階)
ロケット花火による動力飛行→滑空 からなる飛行の1サイクルのを考えます。
ここでは同じく初期条件の速度$${\overrightharpoon{v}=0}$$、位置 $${\overrightharpoon{x}=0}$$ からシミュレーションを開始します。$${0 < t ≤ 25[\mathrm{tick}]}$$ の間、上向きの一定のピッチ角( $${-89\degree≤\phi≤-1\degree}$$ )でロケット花火による動力飛行を行い、それ以降は前段階と異なる一定のピッチ角( $${-89\degree≤\phi≤89\degree}$$ )で滑空を行います。初期の高度 $${y=0}$$ に戻れば1サイクルは終了し、シミュレーションを打ち切ってデータを記録します。
以下の図2では飛距離 $${x_{max}}$$ と平均水平速度 $${v_{avg}}$$ の分布を色で示します。 $${v_{avg}}$$ は飛距離と総飛行時間の比であり、以下のように求めます。
$$
{v_{avg} = \frac{x_{max}}{t_{max}}}
$$
ここで動力飛行時のピッチ角を $${\phi_{f}}$$ 、滑空時のピッチ角を $${\phi_d}$$ とします。
最大飛距離は $${x_{max}=708.9883\mathrm{[m]}}$$ で、この時の平均速度は $${v_{avg}=21.5\mathrm{[m/s]}}$$ 。


図2 動力飛行時のピッチ角 φ_f(x軸)、滑空時のピッチ角 φ_d(y軸)に対する飛距離 x_max と平均水平速度 v_avg の分布
注)x軸は左右反転してあります
以上の図より、こちらに関しては割と当然の結果直観に即した結果ではないかと思います。
図(a)より、動力飛行時ピッチ角 $${\phi_{f}=-77\degree}$$ 、滑空時ピッチ角を $${\phi_{d}=-1\degree}$$ では $${x_{max}}$$ が最大値となっていることがわかり、燃費効率が最大になると考えられます。また、最大値近傍を見ると、最大値の山がx軸方向(動力飛行時ピッチ角)に広く伸びている一方で、y軸方向(滑空時ピッチ角)には狭く、$${\phi_{d}=0\degree}$$ を境に不連続な分布になっています。特に滑空時ピッチ角上向き側では、ピッチを上げると一気に $${x_{max}}$$ が降下してしまうことがわかります。
図(b)から見てとれるように、平均速度 $${v_{avg}}$$ は $${\phi_{d}=0\degree}$$ を境に上半分が全体的に高く、下半分が全体的に低くなっています。これは滑空時の挙動が原因であると考えられ、図1にも同じ傾向が見られます。また $${\phi_{d}>0}$$ 域では左側が $${v_{avg}}$$ の値が大きくなっています。これはロケット花火使用時の速度がどこを向いても一定で、上ではなく前に向けると、当然サイクル全体の平均速度が上がります。このことより、動力飛行時ピッチ角 $${\phi_{f}}$$ が燃費と飛行速度のトレードオフになると考えられます。
この結果は以下のサイトとよく一致しています。(なおこちらはロケット花火を2回打ちで、平均速度(耐久値効率)に焦点を当てています)
https://pillow.rscheme.org/blog/2017-05-15-minecraft-rocket-powered-elytra-efficiency/
4.3 動力飛行(3段階)
ロケット花火による動力飛行→運動エネルギーの回生(上昇/垂直速度が正の値)→滑空(下降/垂直速度が負の値) からなる飛行の1サイクルのを考えます。
ここでは同じく初期条件の速度$${\overrightharpoon{v}=0}$$、位置 $${\overrightharpoon{x}=0}$$ からシミュレーションを開始します。$${0 < t ≤ 25[\mathrm{tick}]}$$ の間、上向きの一定のピッチ角 $${\phi_{f}}$$ ( $${-89\degree≤{\phi_{f}}≤-1\degree}$$ )でロケット花火による動力飛行を行った後、残った運動エネルギーの一部を位置エネルギーに変換するために上向きのピッチ角 $${-89\degree≤{\phi_{a}}≤-1\degree}$$ を維持し、それ以降は一定のピッチ角(燃費の最大化に注目するので $${\phi_{d}=0}$$ で固定)で滑空を行います。初期の高度 $${y=0}$$ に戻れば1サイクルは終了し、シミュレーションを打ち切ってデータを記録します。
以下の図3では飛距離 $${x_{max}}$$ と平均水平速度 $${v_{avg}}$$ の分布を色で示します。点線の斜線は $${\phi_{f}=\phi_{a}}$$ の条件を示しており、動力飛行→運動エネルギー回生を同一ピッチで飛び続ける実用的な飛行プロファイルとなります。(以降では4.2と区別するために「回生2段階」と呼びます。)


図3 動力飛行時のピッチ角 φ_f(x軸)、回生時のピッチ角 φ_a(y軸)に対する飛距離 x_max と平均水平速度 v_avg の分布
点線は回生2段階飛行の条件φ_f=φ_aを示す
注)x, y軸はスケール反転してあります
図3で示した結果から、3段階飛行では2段階飛行よりも飛距離の改善が見られ、同時に、燃費最適飛行における平均速度も増加しました。世の中こんなおいしい話あるんだ
3段階飛行で得られた最大飛距離は $${x_{max}=843\mathrm{[m]}}$$ で、この時の平均速度は $${v_{avg}=25.7\mathrm{[m/s]}}$$ です。図(a)にも示すように、動力飛行時ピッチ角 $${\phi_{f}=-49\degree}$$ 、回生時ピッチ角 $${\phi_{a}=-25\degree}$$ では $${x_{max}}$$ が最大値となっていることがわかります。
回生2段階飛行においても(普通の)2段階飛行より飛距離と燃費最適飛行における平均速度ともに向上することがわかりました。図4では $${\phi_{f}}$$ に対する $${x_{max}}$$ と $${v_{avg}}$$ を示す。
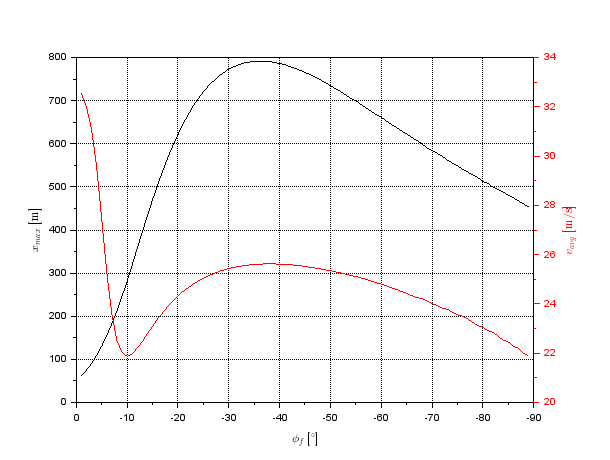
図4からわかるように、 $${x_{max}}$$ のピーク(最大値)と $${v_{avg}}$$ のピークの一つ(極大値)がちょうど重なっていて、燃費最適飛行時でも平均速度は十分速く、実際、最適飛行時の $${\phi_{f}=-37\degree}$$、 $${x_{max}=792\ \mathrm{[m]}}$$ において $${v_{avg}=25.6\ \mathrm{[m/s]}}$$ の値を取っていて、2段階飛行と比較して両方改善したことがわかりました。また最大値附近は緩やかなピークなので、 $${30\degree<|\phi_{f}|<40\degree}$$ の範囲内のどこを取っても大きく効果が減少することはありません。
また $${\phi_{f}=0\degree}$$ 付近では $${v_{avg}}$$ が最大値を取っていますが、ロケットを水平に打っているだけなので自明です。
本当に美味しい話すぎるので検算したいという方は大歓迎です。おそらく間違いはないようには再三にわたって確認したつもりでいます。
4.4 おまけ:成績係数
ここでは詳しく説明しませんが、飛距離 $${x_{max}}$$ 平均速度 $${v_{avg}}$$ の結果をブレンドすることでいい塩梅を取ることもできます。
筆者はここで足し算の重み平均ではなく、以下の式のような掛け算の平均を用います。(そもそも平均とは言わないかもしれませんが私も名前知りません)
$$
{perf = {x_{max}}^{C_{1}}{v_{avg}}^{C_{2}}}
$$
上式で得た成績係数の結果を図5で図示します。
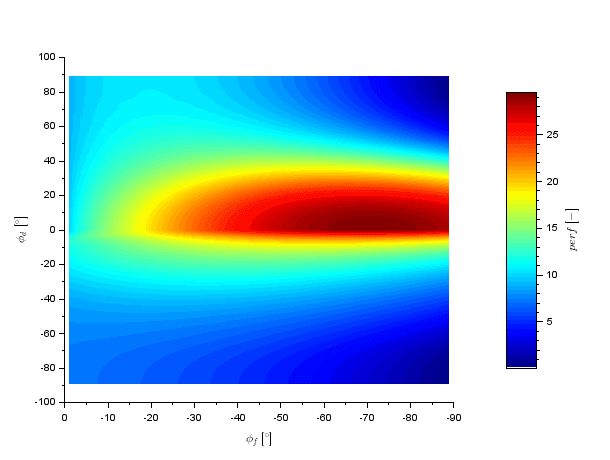

図5 成績係数の計算結果 (C1=C2=0.5)
5. 結論
本研究(?)ではScilab上の計算シミュレーションを用いて、エリトラの燃費最適飛行を求めました。定常滑空飛行の結果に基づいて動力飛行の2段階飛行を解析し、また、3段階飛行(並びに回生2段階飛行)を提案し、2段階飛行よりも飛距離(燃費)とともに平均速度を改善することができました。
実用的な数字を出すと、
2段階飛行では $${\phi_{f}=-77\degree}$$ → $${\phi_{d}=-1\degree}$$、
3段階飛行では $${\phi_{f}=-49\degree}$$ → $${\phi_{a}=-25\degree}$$ → $${\phi_{d}=0\degree}$$ 、
回生2段階飛行では $${\phi_{f}=\phi_{a}=-37\degree}$$ → $${\phi_{d}=0\degree}$$
を目指して飛行してください。
あとがき:F3開いてあるいはHUD MODなどを使ってどんどんやってみてください。
実際はロケット花火の起動時間ガチャもありますがそれでも実感としてはかなり花火節約してると感じました。
また回生2段階飛行は角度をキープしているので花火の連打もより効率的になるかと思います。(感覚的な感想でしかないので要検証)
追記(2024/7/10):エリトラ「回生」挙動の実例
私がこの挙動を発見したのは偶然のことでした。FlightHUDという戦闘機のHUDみたいなのが出るModを入れていて、そのModでは姿勢の表示だけでなく速度ベクトルがどこ向いているかも表示してくれます。
ところがある日、スピードを上げて滑空した後に20~30度程度に頭上げの姿勢を取ると、急に速度ベクトルが頭上げ分以上に上を向いてくることを発見しました。マイクラの疑似揚力は侮れない
実際の飛行軌跡を見るために、4.3項の回生2段階飛行の単発シミュレーション( $${\phi_{f}=\phi_{a}=-35\degree}$$ )を行い、tickごとの速度と位置ベクトルのデータを記録しました。時間に対する速度と位置の鉛直(y)成分を図6で示しています。
図では $${t=25\ \mathrm{[tick]} = 1.25\ \mathrm{[s]}}$$ 以降、ロケット花火による速度制約(視点方向に一定の終端速度)が外れ、鉛直速度が突然上昇する様子が見て取れます。余った運動エネルギーが位置エネルギーに変換される(保存則が成り立っているかは要検証)ことからこの挙動を「回生」と名付けることにしました。
実際の原理までは踏み込めなかったですが、実態としてはこのような結果となっています。

