降圧スイッチング電源の入出力電圧[詳細導出過程有り]

本記事では、PWM制御をする非絶縁降圧スイッチング電源回路の入出力電圧関係式の導出方法を解説します。

今回導出する式と導出の流れ

最終的に導出する式を先に提示します。
入出力関係式：Vo＝DUTY×Vin
Vo：出力電圧[V]
DUTY：1周期あたりのON時間の割合[%]
Vin：入力電圧[V]

導出の流れは以下の通りです。
①定常状態=出力電圧Voが既に一定の電圧になっていることを想定する
②スイッチがONのときとOFFのとき、それぞれの回路を描く
③それぞれの回路の電流の流れとコイルの両端電圧を考える
④V=Ldi/dtの式を使って、ON時の電流増加分とOFF時の電流増加分の式を立てる
⑤上の式をイコールで解いていく

正直これらの式を覚えるより大事だと思うこと。

個人的にはこれらの式より「スイッチON／OFF1周期のコイル電流増減分は等しくなる」という考え方を覚えるべきだと思います。これだけ覚えていると回路形式が変わっても導出出来ます。

降圧スイッチング電源の回路構成

まず、対象の回路を確認します。

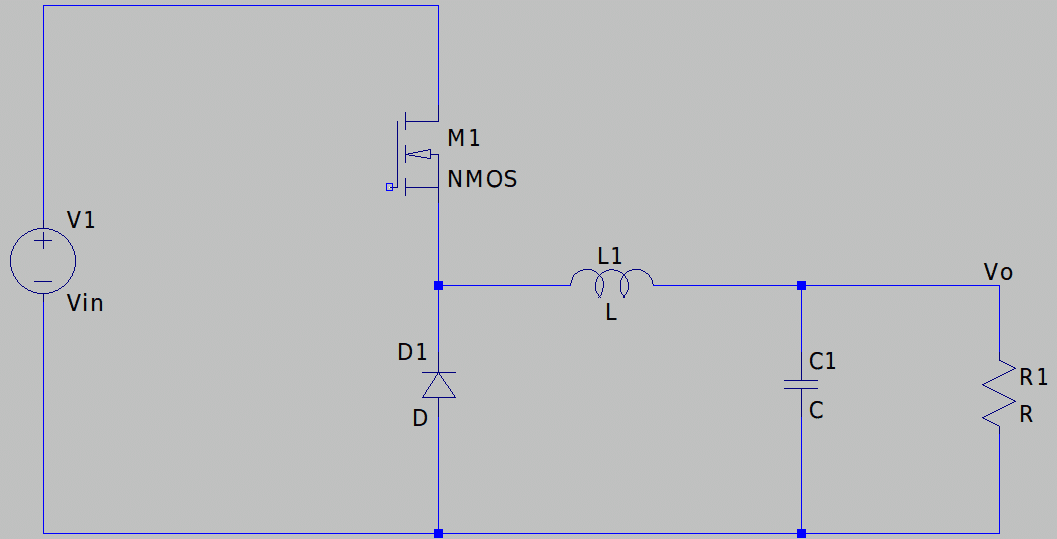
動作としてはスイッチM1をON/OFFを繰り返します。このON時間、OFF時間を調整してVoを一定電圧にします。

事前知識

コイルの式：V＝L×di/dt
高校？中学？の物理で出てきますね。私は未だによく忘れます。まぁ忘れたら調べればいいだけです。それでは、導出をやっていきましょう。

①定常状態=出力電圧Voが既に一定の電圧になっていることを想定する。

最初にスイッチング電源の動きを勉強しようとする人の中には、Vo=0[V]と想定してどうVoが所望の電圧に上がっていくんだろう。。。と考える人がいるかも知れません(昔の私がそうでした。)が、入出力電圧の関係やコイル電流を考えるときにはVoは既に所望の電圧が得られていると想定しなければ導出できません。ここは一旦、Vo=Vo[V]なんだ！！と置いてください。

②スイッチがONのときとOFFのとき、それぞれの回路を描く。

SW=ON/OFFのときに回路がどうなるかを分けて考えます。
SW=ONのときは簡単で電源と繋がってる回路を描けば良いです。
問題はSW=OFFのときです。このときは下に繋がっているダイオードがONします。回路図は以下のようになります。(ダイオードがONするとVf電圧0.数[V]が生じて正確には繋がった状態にはなりませんが、今は簡単のために0[V]とします。)

なぜ、SW=OFFのときはダイオードがONするのでしょうか。これはコイルの特性によるものです。コイルは「電流を流そうとすると拒んで、流すのをやめようとすると流し続けようとする」性質があります。
つまりどういうことかというと、SW=ONのときは電源からコイルに電流が流れます。そのときコイルは流すまいとして、ゆっくり電流が上がっていきます。それがSW=OFFとなり電力供給がなくなるとコイルは逆に電流を流し続けようとします。でも電源からは電流を流せないので、ダイオードがONするまでコイルの左端電圧を下げてダイオードから電流を引っ張ります。
ここが初めて勉強する方には最も難しいところではないかと思います。「電流を引っ張る？」、「左端電圧が下がって、右端がVo[V]なら電流流れないんじゃね？電流は電圧が大きいところから小さいところに流れるんだから。」と私は最初全然納得出来ませんでした。でもコイルがいるとこういうことが起こります。最初はイメージしづらいですが、何度も動作を見ているとなんとなく掴めていくと思います。

③それぞれの回路の電流の流れとコイルの両端電圧を考える

まず簡単なSW=ONのときを考えます。これは電源からコイルに向かって電流が流れます。コイルの両端電圧はVinとVoになります。
次にSW=OFFのときはコイルが電流を流し続けようとして、ダイオードがONしてダイオードから電流が流れます。このときコイルの両端電圧は0[V]とVoになります。

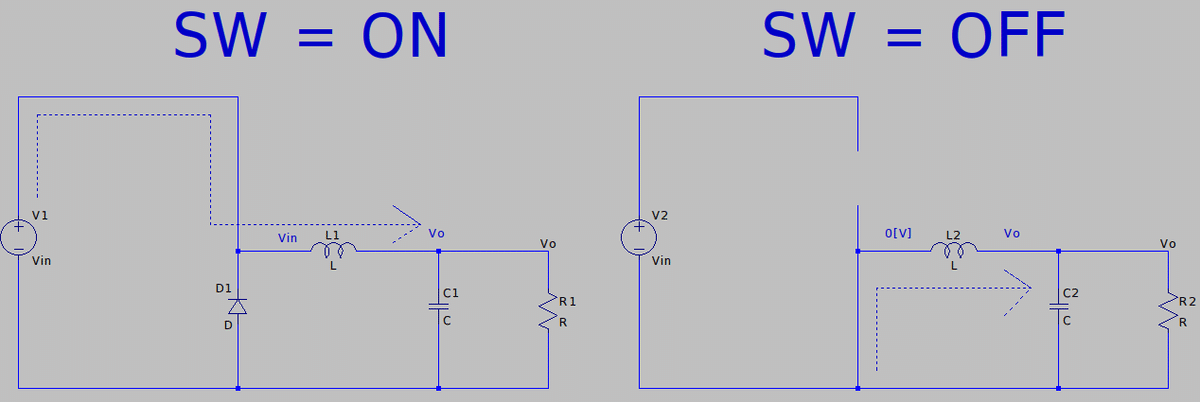
SW=ONのときはLにはVin - Voの電圧がかかっており、
SW=OFFのときはLには0 - Voの電圧がかかっております。
Vo - 0ではありません。電流の向かう方向に計算していくので、0 - Voです。

④V=Ldi/dtの式を使って、ON時の電流増加分とOFF時の電流増加分の式を立てる

di/dtは何か難しく感じますが、diとは電流増加分=Δi、dtとは経過時間のこと。ON時間をton[sec]、OFF時間をtoff[sec]と書いて差し支えありません。
まずはこの式を電流増加を求める式に変形します。

Δion = V / L × ton
Δioff = V / L × toff

このVとはコイルにかかる電圧、つまりコイル両端電圧の差分です。
③を見返して、ONのときOFFのときの両端電圧の差分をVに代入します。

Δion = (Vin - Vo) / L × ton
Δioff = (0 - Vo) / L × toff

これがON時、OFF時の電流増減分を表した式になります。
SW=ONの式をみると、(Vin-Vo)/LはVin>Voなので、正の定数になります。つまりΔionはtonに応じて右肩上がりに一定に上がっていくことがわかります。
一方SW=OFFの式では-Vo/Lは負の定数になります。こちらはtoffに応じて右肩下がりに一定に下がっていくことがわかります。
この電流の関係を図に描くと以下のようになります。

⑤上の式をイコールで解いていく。

あとは上で立てた式を繋いで、解いていくだけです。
まず、Δion + Δioff = 0になることを利用して式を立てます。

(Vin - Vo) / L × ton + (-Vo) / L × toff = 0

この式をVo=〜の式に直したら、最初に提示した式が得られます。
一旦Δioff項を右辺に持っていきましょうか。

(Vin - Vo) / L × ton = Vo / L × toff

Lが消せそうなので、消します。

(Vin - Vo) × ton = Vo × toff

左辺を分解します。

Vin×ton - Vo×ton = Vo×toff

Voでまとめます。

Vin×ton = (ton + toff) Vo

ton + toffで両辺を割ります。ついでに左辺と右辺を入れ替えます。

Vo = ton/(ton + toff) × Vin

ton + toffは1周期を表しており、ton/(ton + toff)は1周期間のON時間の割合を表しています。これを表す言葉にDUTY[%]というものがあります。これに置き換えると

Vo = DUTY × Vin

と最初に提示した式が導出されます。

まとめ

入出力電圧の関係式：Vo=DUTY×Vin
この式はON/OFF時のコイル電流の増減分が等しいという考え方で立式していけば、導出できます。
個人的にはOFFのときに0[V]からVo[V]に電流が流れるというのが、初めての方には掴みづらいところなのかなぁと思います。私はコイルは天邪鬼なやつだと思い自分を納得させました。。。