第37章　分数のわり算がムズすぎる話・後編

昨日は勢いに任せて「分数のわり算は一生使わない」という話を書いたのですが、少し補足というか、小学校でなぜ分数のわり算を習うのかという話の私なりの解釈を書こうと思います。

分数のわり算に込められている数学的な意味についてです。
実は、分数のわり算には「逆演算」と「逆数」という概念が込められています。
順を追って説明しますね。

1. 逆演算とは

難しく考える必要はありません。
例えば「ひき算」は「たし算」の逆演算です。

この式の四角に入る数字を求めるとき、3 に何を足せば 5 になるか、というのを計算するのが「ひき算」です。
つまり、下のような式の四角に入る数字を計算します。

答えは 2 ですよね。
たし算は可換なので 3 と四角の順番が逆でも問題ありません。
つまり、下みたいな式を書いても一緒です。

せっかくなので小さい数から大きい数を引く場合も考えてみましょう。

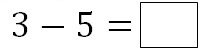
これは小学校では「ひけない」と習いますが、中学校では 0 よりも小さい「負の数」の概念を習うので解くことができます。
やることは同じです。

5 に何を足せば 3 になるか、0 よりも大きい「正の数」ではありえないので、答えは負の数の中にあります。
答えは −2 ですね。

以上が、「たし算」とその逆演算である「ひき算」の関係です。
「かけ算」と「わり算」の関係も同じです。「わり算」は「かけ算」の逆演算ということになります。

上のような式の四角に入る数値を求めるとき、3 に何をかければ 6 になるか、というのを計算するのが「わり算」です。
つまり、下のような式の四角に入る数字を計算します。

答えは 2 ですよね。
かけ算もたし算と同じく可換なので 3 と四角の順番が逆でも問題ありません。
ためしに下みたいな式を書いても答えは同じになるのがわかると思います。

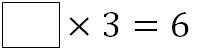
それでは、次のような式はどうでしょう？

小学校では最初、2 あまり 1 というふうに習うと思います。
わりきれない数の場合は「あまり」が発生します。
2 が「商」で、1 が「あまり」。
わりきれるかどうかを判断できるというのは重要で、これは「因数」の概念を理解する助けになりますし、中学校で習う「因数分解」の基礎になります。
一次関数 y=ax + b のグラフの切片を求めるときにも使います。

というわけで、重要ではあるんですが、二つも数字が出てくるのはちょっと面倒くさいですよね。
さっきまでの逆演算の考え方で見てみましょう。

この式の四角に入るのは商の 2 でもなければ、あまりの 1 でもありません。
無理やり書くとこうなります。

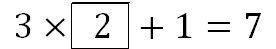
たし算がまざっちゃって、あまり美しくないですね。
ここで活躍するのが「分数」です。
四角に当てはまる便利な数字を作ってしまったわけです。

まずは説明を簡単にするために、ちょっとだけ式を変えます。

これを計算するのに逆演算の式を考えると

わからないので、ためしに逆にしてみても

やっぱり当てはまる数がありません。
ここでこんな数字を作りました。

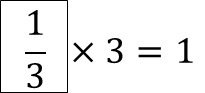
3 をかけたら 1 になる数を 3 分の 1 という数字にしましょう。

なんじゃそら！

と思うかもしれませんが、これが使ってみたら結構便利です。
割れない数字を割らないといけない場面は結構あります。
例えば、1 個のケーキを 3 人で平等にわけないといけないとき。
3 分の 1 個ずつ切り分けるとちょうどいいですよね。

一応ねんのため、かける順を逆にしても同じく成り立ちます。

7 を 3 でわるときも同じように分数を使います。

3 をかけたら 7 になる数を 3 分の 7 という数字ということにすれば、われなかった数がわれるようになって解決です。

これが「分数」が生まれた理由です。
分数に対して、3 や 7 のような数字を「整数」と呼びます。
さすがにそれは知ってますね。

2. 分数のかけ算

分数が生まれた理由がわかったところで、まずは分数のかけ算についてです。
分数をかけ算するとどうなるんでしょう？
分数のルールを紐解きながら解説します。

まずこれは余裕ですよね。答えは 1 です。
だってそういうルールで分数を作ったわけですから当然です。

これも余裕ですよね。答えは 2 です。
この分数の横棒の上の数を「分子」って呼びますよね。化学に出てくる分子と同じ字なのでちょっとややこしいですが。
下の数は「分母」です。
それでは続けましょう。

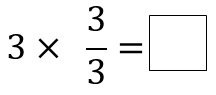
これの答えは当然 3 です。つまり

ここで気づいてほしいのは、

この計算で四角に入るのは 1 ですよね？
ということは 3 分の 3 は 1 と同じということになります。
これはもちろん当たり前です。
3 をかけたら □ になる数を 3 分の □ という数字ということにしたのが分数ですから、3 をかけたら 3 になる数である 3 分の 3 は 1 と同じ意味です。

こういう当たり前のことを確認するのは数学のルールを作る上で大事です。
別の角度から見ても矛盾しないことが数学のルールの大前提です。
それでは続けますよ。

なんとなく法則が見えてきますね。
3 分の 6 は 2 と同じだし、3 分の 9 は 3 と同じです。
分子の数が分母の数でわりきれるとき、分数は整数と同じになります。

それではちょっと応用問題です。

急にむずかしくなりましたね。
はてさてどうしてくれよう…。

「バカにするな」という声が聞こえてきそうです。
さすがに知ってますよね。答えはこうです。

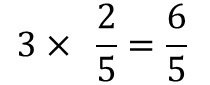
小学校3年生以上ならほとんどの人が解ける当たり前の計算ですが、なんでこの計算があってると言えるのでしょうか？
いったん、小学校で習った分数の計算のルールを忘れて(使わずに)、ここまでに決めたルールだけで考えてみましょう。
図を描いたりして説明すれば理解できることも多いですが、ここはあえて分数の成り立ちの話を使って考えてみます。

5 をかけたら 1 になる数を 5 分の 1 というルールにしましたよね。
5 をかけるということをたし算であらわすと下のようになります。

5 分の 1 を 5 回たしたら 1 になるわけです。
そして思い出してください。1 は 5 分の 5 と同じでした。
つまり、式で書くと

こういうことになりますよね。
5 分の 1 を 5 回たしたら 5 分の 5 になることがわかりました。
では、5 分の 1 を 3 回たしたらどうなりますか？

なんとなく 5 分の 3 になりそうな気がしますね。
でもまだ分数のたし算のルールを決めていなかったので、本当にそうなるかわかりません。確かめてみましょう。

5 をかけたら 3 になる数が 5 分の 3 でした。

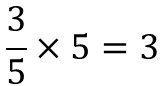
つまり 5 分の 3 を 5 回たせば 3 になるはずです。

ここで、5 分の 1 を 5 回たしたら 1 だったので、それを 3 セット
つまり 5 分の 1 を 15 回たしたら 3 になるはずです。

めちゃくちゃ長い式になりました。

こう書いたら楽ですよね。かけ算って便利！
でも、今はたし算のまま式をいじります。
ここでいったん、5 分の 1 を 3 回たした数に戻ります。

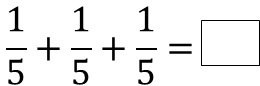
これ、とりあえず答えがわからないものとして四角で表します。
5 分の 1 を 3 回たした数を四角として、5 分の 1 を 15 回たした式にあてはめてみます。

四角を 5 回たしたら 3 になることがわかりました。
これってつまり、5 をかけたら 3 になる数ということですよね。

つまり、四角に入る数は 5 分の 3 です。

みんなが当たり前だと思っていることが、やっぱり正しいことが証明されました。
この理屈でいけば、少なくとも分母が同じ分数のたし算であれば問題なく同じ計算が成り立つはずです。
つまり

ですから、

となりますし、かけ算は可換なので

も同様に成り立ちます。
ここでわかることは、分数と整数のかけ算では、分数の分母はそのままに、分数の分子と整数をかけたら答えが求まるということです。
みんなが小学校で習って計算方法は知っているはずですが、証明するのには手間取りました。

ここでもう一つ面白い性質があります。
6 をかけたら 2 になる数を分数で表してみましょう。

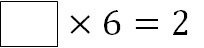
これまでの話から、素直に考えると四角に当てはまるのは 6 分の 2 ということになります。

でもちょっと待ってください。

これも成り立ちますよね。だって、上の方で紹介した通り 3 分の 6 は 2 ですから。というわけで

この二つの分数は同じものだということがわかりました。
3 分の 1 の分母と分子に 2 をかけたら 6 分の 2 になり、6 分の 2 の分母と分子を 2 でわれば 3 分の 1 になる点に注目してください。
この組み合わせに限らず、分母と分子に同じ数字をかけたものは、同じ分数ということになります。
分数の分母と分子が同じ数でわれる場合に、わって見た目の数字を小さくすることを「約分」と呼びます。
逆に、分数の分母の数字をそろえてたし算、ひき算の計算ができるように調整することを「通分」と呼びます。
約分や通分をしてもその分数は元の分数と同じ数です。

それでは、次はようやく分数同士のかけ算です。

お、おう・・・
強敵あらわる。

できますか？
さすがにこの計算は知っているという前提で、話を進めますね。

この計算はほとんどの人が問題なくできるものですが、じゃあ、なんでこんな計算になるのか、これまでのルールで説明できますか？

◯が△個みたいな話をするとき、△の中にはふつう整数が入りますよね。
△に分数が入ると、とたんにイメージしづらくなります。

しょうがないので、かけ算の「分配法則」というものを使います。
まず分配法則について説明しましょう。

これは九九ができれば誰でもできる計算です。

これももちろん余裕ですよね。
さて、6 は 2 を 3 回たしたものと同じです。

これを 5 × 6 の式に照らし合わせたときに

こうやって分解することができます。
つまり 5 × 6 の計算結果と 5 × 2 を 3 回たしあわせた計算結果は同じなのです。
これは、6 が 2 を 3 回たしたものとして分解できるからです。
これをかけ算の分配法則と呼びます。
ふつう整数のかけ算をするときに、こんな面倒くさいことをする人はいないと思うのですが、これが分数のかけ算のときには役立ちます。

さて、この式を分配法則で分解してみましょう。

上の式を使います。

4 つの同じかけ算に分解できました。
これで、この赤い点線でかこったかけ算さえできれば、答えが出せそうです。というわけであらためて

この式の答えについて考えてみましょう。
このままだとやっぱりわかりませんので、分数のルールを思い出してみます。
3 をかけたら 1 になる数が 3 分の 1 でした。
上のセットを 3 つたしてみましょう。

ここで

ですから、さっきと逆の手順で分配法則を使います。
つまりこうなります。

今、かなりややこしいことをやったように見えたかも知れませんが、分配法則の逆の手順を使っただけです。下から順に式を見てもらえればわかります。
というわけで、四角を 3 つたしたものと 3 分の 2 が等しいということがわかりました。
今の流れ、さりげなく方程式を使ったんですが、まあバレなきゃイカサマじゃないってことで許してください。

つまりこういうことです。

さらにかけ算になおすとこうなります。

だいぶすっきりしましたけど、まだ問題があります。
3 をかけて 3 分の 2 になる数って無くない？
実はあるんですよね。
約分・通分の出番です。
3 分の 2 の分母と分子にそれぞれ 3 をかけて通分してやります。

これなら問題なくできますね。

ようやく、上の方の式で出てきた赤い点線でかこった部分の答えが出ました。

あとはこれを 4 回たす（4 をかける）だけですので

・・・できた！
長かった！

で、この計算の途中の過程をよくよく見てみると、結局のところ分子同士と分母同士をかけただけなんですよね。
たったこれだけのことを理由をちゃんと説明するの、難しいですね。
まあ、私の能力不足のせいかもしれません。

さて、ようやくかけ算ができたところで、いよいよ本題の分数のわり算です。

3. 逆数の話

小学校で習う分数のかけ算の話で、ずいぶんと長々と話してしまいました。
わり算についてはさらっと行かせてもらいます。

だって一生使わないですから。

とはいえ、これから話す逆数の概念は数学をやる限り使うことになるので、その話を中心にしたいと思います。

もう、おわかりかと思いますが、わり算はかけ算の逆演算です。

この計算をするとき、小学校では「分母と分子をひっくり返してかける」と習いますよね。
なんでそんなことをするのか、そんなことをしてなんで正しい答えが出てくるのか、理由は逆数の性質にあります。

「逆数」とは、ある数にかけて 1 になる数のことです。

3 の逆数は 3 分の 1 です。
3 分の 1 の逆数は 3 です。

わかりにくいという人は式の順番を換えてみてください。
お互いに逆数の関係になっているのはわかりますよね。

3 分の 4 の逆数は 4 分の 3 です。
分数は分母と分子をひっくり返したら逆数の関係になっています。
この計算結果が正しいとすぐ判断できない人は実際に計算してみてください。
ちゃんと 1 になります。

それでは分数のわり算です。

3 分の 2 を 3 分の 4 でわるということは、3 分の 4 をかけて 3 分の 2 になる数を求めるのと同じです。

式の両辺に 4 分の 3 をかけてみてください。

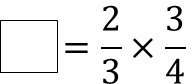
ほら、3 分の 4 でわることは、逆数の 4 分の 3 をかけるのと同じになっているでしょ。
これが「ひっくり返してかける」理由です。
今、もう隠すことなく方程式と同じ演算をやって見せたわけですが、方程式を解くときには、まさにこうやって逆数をかけて分数を 1 にしてしまうという演算をやることが多いです。
もしかしたら、方程式を解くときに「かけ算だから移項してわり算にして」みたいなことをやっている人がいるかもしれませんが、そんなことせずに「両辺に逆数をかける」で全部片付くんですよね。

だから、分数のわり算なんて要らんのですわ。
もう一回言いますけど、「一生使わん」。

4. 最後に

想定よりだいぶ長くなってしまいました。
かけ算はちょっと丁寧にやったほうがいいかなと思ったので。
小学校でこの「分数のわり算」を習う理由について考えてみましたけど、おそらくは

• 「かけ算」をやるのにその逆演算の「わり算」をやらんわけにはいかん

• 「逆数」の概念の導入？

• 分数に対する理解を深める？

あたりかなと思うんですが、正直、理解できている人があまりいないことを考えると、やっぱりやらんでええんとちゃいますかね？
やるなら、「逆数」の概念からちゃんと教えるべきだと思います。
勘の良い人はとっくに気づいてると思いますが、「かけ算」の逆演算は「わり算」ですが、「逆数をかける」ことと同じになっています。
別に「分数のわり算」に限らず、「わり算」と「逆数をかける」は同じ演算です。
そしてそれが分数の成り立ちと結びついてるわけです。

こういうことも含めて「いや、ちゃんと小学校で教えてるよ」ということならごめんなさい。

以上です。