弧度法は円周上の長さの指標である
弧度法はいったいどんな用途で使用できるのかを伝えたいと思います。
前書き
私が高校の時代、弧度法は数学Ⅲで学びますが、その当時は数学Ⅲは選択式だった。しかし、私は数学Ⅲを選ばなかったので、独学で数学Ⅲを学んだ。(私は当たり前のように弧度法を使ってきたが、よくよく考えれば学校で教わらなかったことを今になって思い出した。)その私が、弧度法が何のためにあるのかを簡単にお伝えする記事です。
最も、数学Ⅲを学ぶ高校生からすれば当たり前の内容なのですが、実際に弧度法による計算を用いると、3DCADデータを作成するうえですごく便利です。弧度法の本来の目的を明らかにする形で伝えることができればと思います。
弧度法とは何か
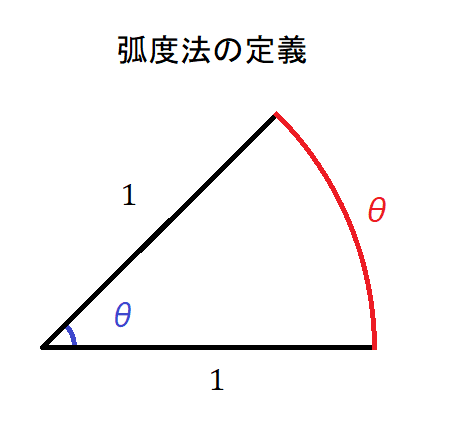
弧度法とは、任意の扇形の半径を1にしたときの弧の長さであり、それを「角度」と呼んだものが弧度法です。ですから、
弧の長さ=弧度法の角度×半径
になります。
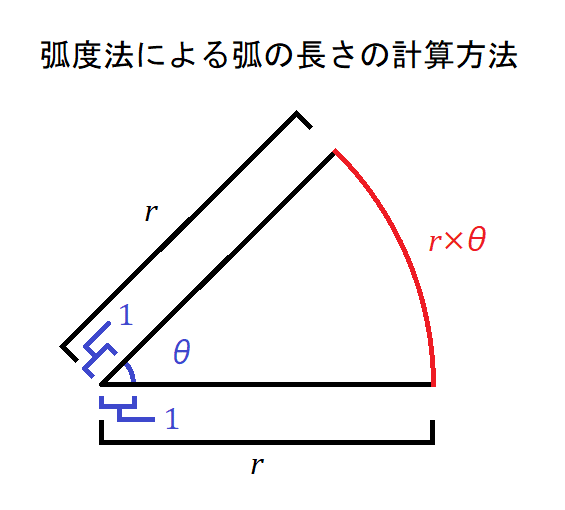
度数法の360度が弧度法の2πなのは、上記の説明の通り、半径1の円の円周が2πだからです。
CADソフトが弧度法に対応していない場合は、度数法に単位変換を都度してあげれば問題ありません。
役立つ場面
円周上の距離を測る面で役立ちます。例えば、直線に引き伸ばした状態で1センチであっても、半径3センチの円周上では曲がっているので、それに沿って厳密な位置を計算します。

例えば、地球上で測定する場合、小さい値であれば距離を直線として捉えますが、丸い地球で大きなスケールでの測定を行いたければ、
地球上の距離=地球の中心からの角度×地球の半径
という解釈になります。丸い対象に這わせて扱う場合には弧度法を用いることができます。
まとめ
弧度法とは、扇の半径を1にしたときの弧の長さである。
弧の長さ=弧度法の角度×半径
円周上の長さや位置を測定する面で役立つ。
いいなと思ったら応援しよう!