
オーケイ、この宇宙は計算可能だ——『プロジェクト・ヘイル・メアリー』の精緻な世界を無粋にも計算してみる
計算せずにはいられない、いますぐ計算したい。
警告! この記事には小説『プロジェクト・ヘイル・メアリー』のネタバレが大量に含まれている。
だから『プロジェクト・ヘイル・メアリー』を読了後に読んでほしい。ふだんなら「ネタバレを許容できる人だけ〜」という言い方をするのだが、今回ばかりは強く訴える。なにしろ原作が、ネタバレ厳禁なタイプの作品だからだ。
読んでない人は、まずは原作を読んでみてほしい。話はそれからだ。下のリンクをクリックするだけだ。
ちなみに映画版については、この記事の対象外だ。なにしろ、まだ「製作中」だからね! ——とのんびりしていたら、数日前に映画がクランクインを迎えてしまった! こいつはまずい。映画の情報がどんどん出てきたら、この記事は無意味になってしまうかもしれない。執筆を加速させなければ……
LET’S GOOOOOOOO pic.twitter.com/mRlf3rpccF
— Christopher Miller (@chrizmillr) June 3, 2024
まあ、そんなことはどうでもいい。ともかく、いいたいのは「ネタバレ注意」ということだ。
覚悟はいいか?
……オーケイ。
それでは、ネタバレ全開で行くことにする。
この記事は何がしたいのか? なぜこんな酔狂な記事を書いているのか?
このnoteは、アンディ・ウィアーのSF小説『プロジェクト・ヘイル・メアリー』(以下、PHMと呼ぶ)に出てくるあれやこれやを、ざっくり計算してみよう! という非常に酔狂な記事だ。
見よう見まねで計算して「うわあ! アンディ・ウィアー、ガチで設定作り込んでる!」と驚いて楽しむのが目的だ。彼がガチ勢であることは『火星の人』のときからわかってた話だけど、今回やってみたら予想以上にガチだとわかったので、せっかくなので記事にしてみたってだけの話だ。
* * *
ウィアー作品の主人公は、とにかく計算しまくる。まあ、どれも極限状態で生き延びるために必要な計算なので必然ではあるのだが。
計算だらけでうんざりだという読者も多いかもしれないが、個人的にはすごく好きな姿勢だ。科学への強い信頼を感じるし、作品世界そのもののリアリティラインが爆上がりするからだ。
記憶喪失の主人公は、どうやって自分の置かれた状況を認識するか? 計算だ。直感とか、情況証拠とかじゃない。完全に計算と物理学の知識だけから、自分が宇宙船の中にいること、他の星系にいることを把握していく。小説の書き出しが「2足す2は?」で始まっているのは、実に象徴的だ。「初めに計算があった(In principio erat Computatio)」。
計算によって世界を理解し、制御していく主人公、ライランド・グレース。計算によって世界を緻密に構築していく作者、アンディ・ウィアー。二人が世界に立ち向かう姿勢に共通しているのは、科学的方法論であり、それを支える計算の数々だ。
とんでもなくクールだと思った。
だから、そのほんの一部でも追体験してみたいと感じたんだ。
これはけっしてふわふわした夢物語なんかじゃない。この世界の延長線上にかれらがいる——ぼくらとかれらの宇宙は地続きで、おなじ物理法則に従っている。ということは、小説に書かれていないことでさえ演繹的に推論できるのだ! それを、手を動かしてたしかめてみたくなった。
幸いにも、この小説には具体的な数字が大量に出てくる。さあ、計算してみろ! と言わんばかりに。数字を見ると検算したくなるのが、理系オタクという生き物だ。
かつて、ロッキーはいった。「計算は考えることではない」と。
計算は考えることではない。計算は手続き。記憶は考えることではない。記憶は貯蔵容量。考えることは考えること。問題、解決。
この記事もそうだ。これは考察とか解説とか、そんなたいそうなものじゃない——なにかを深く考えた結果ではない。ただ決まった「手続き」に沿って、なにも考えず手を動かしてみたってだけだ。考察や解説、レビューは、得意な人におまかせしたい。検証というような、大上段に構えたものでもない。ただのひとり遊びだ。
* * *
言い訳、というか注意点をいくつか書いておく。
この記事はくそ長い。うんざりするほど長い。全部通しで読むのはさすがに苦行だと思うのでお勧めしない。ただの自己満足なのでスルーしてくれてかまわない。ただ、最後の節だけは「PHMをもっと楽しむための情報源」をいろいろ紹介しているので、気が向いたらそこだけ読んでもらえれば個人的には満足だ。ウィアー自身による設定資料の話や続編構想の話などを紹介している。ショートカットはこちらだ(noteアプリやスマホだとうまく飛べないかもしれない。上にある目次から、★をつけた最後の節に飛んでもらったほうがよいかも)。
計算の導出過程を長々と述べるのがこの記事の主眼じゃない。素人がググった式をもってきて、結果だけ比べて、ワオ! 合ってる! すごい! しあわせ、しあわせ、しあわせ! って喜ぶだけの記事だ。専門知識は前提としていない。なにしろ、書いている本人がよくわかっていないのだ。
だから決してマウント目的とかではない。だけど、もしそう感じさせてしまったとしたら申し訳ない。
今回チャレンジしている計算、とくに相対論や天文学については完全に素人だ。正直、中学の理科すらあやしい。必死にググって見つけたそれらしい公式を、よくわからないまま適用しているだけだ。くわえて、英語も不得手だ。たぶん、まちがいだらけだと思う。うん、まちがいだらけにちがいない。バグもあると思う。だから鵜呑みにはしないでほしい。もし少しでも怪しい点を見つけたら、どうか教えてもらえないだろうか。コメント欄からでもツイッター(@alltale2037)からでもいい。こちらとしても、まちがいを堂々と広めたくはない。
厳密な計算はやっていない。ざっと雰囲気をつかめればそれでいいというスタンスだ。ナプキン裏計算とかボールパーク見積もりってやつだ。
計算結果から勝手に類推したことも書いてあるけど、公式見解でもなんでもない、単なる妄想なので、おなじく鵜呑みにはしないでほしい。
計算結果と本文の記載が合わない部分についても書いてある。だけど、「ウィアーの計算はまちがってる!」と言いたいわけでは決してない。たぶんこっちがなにかをまちがえてるんだろうけど、わからないので皆様のお知恵をお借りしたいっていうだけだ。万が一、もしウィアーの計算にまちがいがあったとしても、それを非難するつもりは毛頭ない。ただ、この作品世界をより深く理解したかっただけだし、おもしろさはまったく損なわれない。そもそもこれはフィクションだ。でも、そんな重箱の隅をつつくような指摘をしやがって、と思われる方はいるかもしれない。無粋なのは自覚している。申し訳ない。
内容は科学の中でもかなり物理学に偏っているかもしれない。生物学、特にエリディアンについては、(この記事の最後でも紹介するが)すでにアンディ・ウィアーが設定集を大公開しているので、もはや語るべきことがほとんどない。アストロファージやタウメーバについては気になる点は多いが、情報が少なすぎる。
PHMのファンダムはとんでもなく巨大だ。発刊から数年経ったいま、膨大な情報がそこに集積されているのはうすうす気づいてはいる。Redditとかにはアンディ・ウィアー自身が降臨してたりする。海外はもちろん、国内にも詳しい方がたくさんいるのだと思う。でも、かれらの活動についてはぜんぜん把握できてない。申し訳ない。すでによそで100万回言われている話だらけかもしれないが、許してほしい(むしろ先行研究を教えてください!)。
単に「オーケイ」とか「ワオ」とか言いたいだけの記事なんじゃないかって? うん、そうだな。その推測はきっと正しい。実際、ウィアー作品を読むとなぜか「ワオ」「オーケイ」っていいたくなるんだ。ウィアー作品の文体汚染能力はとんでもなく高い。まるでタウメーバみたいにこっちの言語野のすきまに中途半端に潜り込んでくるんだ。日本語翻訳版には「ワオ」は33回、「オーケイ」にいたっては176回も出てくるから、そのくらいは許してほしい。
最後に、これについては何度でも強調したいが、この記事は決して主人公の「なりきり」とかじゃない。さすがにそんなイタい企画ではない。ライランド・グレースとぼくは完全に別人だ。ぼくは彼とちがってぜんぜん頭もよくないし、科学の知識も乏しいし、行動力もない。単に、最近になってようやくPHMを読んだだけの、そして「オーケイ」って言いまくりたいだけの、頭のいかれた日本人だ。共通点はせいぜい、ダイナーで食べる朝食が大好きだってことくらいだろう。
オーケイ。
まえがきはこのくらいにして、本編をはじめたいと思う。
ライランド・グレースはいったい何歳なんだ?
そもそもぼくが酔狂な計算をやってみようと思い立ったのには、きっかけがある。「ライランド・グレースはいったい何歳なんだ?!」ということが、唐突に気になってしまったからだ。
小説のラストにこんな記述がある。
いま五三歳だと思うが、断言はできない。時間が遅れる旅をだいぶやってきたので。いちおういっておくと、地球では、ぼくが生まれてから七一年の歳月が流れている。これは正確な数字だ。
ラストで53歳(自称)らしいことはわかった。じゃあ小説の大部分を占める、タウ・セチにいたころの彼はいったい何歳なんだ? 彼はいったい何歳のときに地球を出発したことになる? 地球に残った人たちは何歳になっているんだろうか?——
オーケイ。彼のいる状況下では「同時性」なんて概念をもはや日常的な感覚で使えないってことは、なんとなくはわかっている。なにしろ、彼の時間はさんざん遅れまくっているのだ。つまり、特殊相対性理論的解釈が必要ってことだ。
だけどぼくは、相対論なんてまったく学んだことがない。だから、ひたすらググった。幸い、世の中には特殊相対論の公式をわかりやすく解説してくれているサイトがたくさんある。たとえばこれだ。
ここには「一定加速度1Gで加速し、中間点でひっくり返って1Gで減速するロケット」の話がでてくる。ワオ。これを1.5Gにすれば、ヘイル・メアリーそのものだ! ありがたい。というわけで、ここに書いてある式を、意味もわからずそのまま使わせてもらうことにする。
まずタウ・セチやエリダニ40はどこにある?
まず、そもそも、本作に出てくるいろいろな天体は、地球からどのくらい遠いのだろう? それがわからないことには話がはじまらない。目的地までの距離が、時間の遅れに効いてくるからだ。
主人公は、地球からタウ・セチの距離は11.9光年だといっていた。ググって、SIMBADという星のデータベースみたいなものがあるのを知った。おかげで、より正確には11.912光年とわかった。
エリダニ40(一般的にはエリダヌス座オミクロン2星っていうみたいだ)の位置もさっきのSIMBADに出ている。その情報をもとに、まずはソル(ぼくらの太陽)、エリダニ40、タウ・セチの位置関係を、ソルを原点とした銀河座標系で描いてみる。
こんなふうになった。
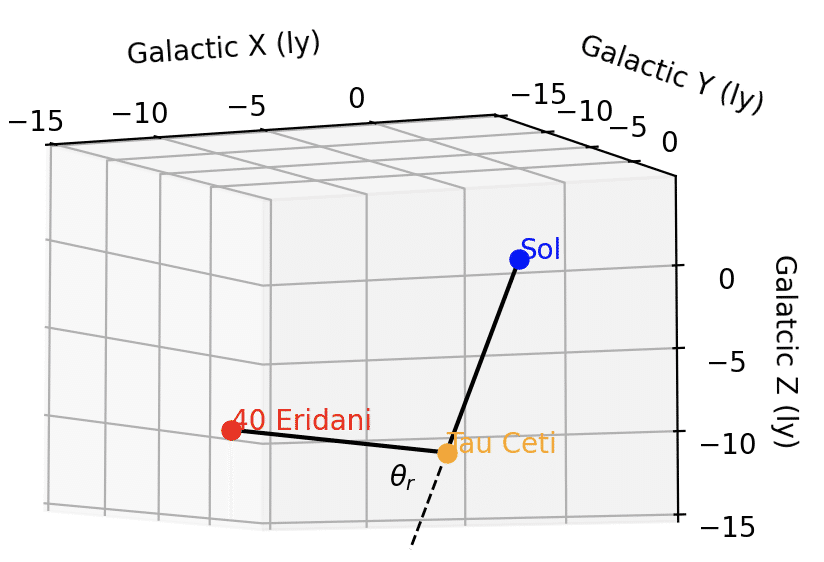
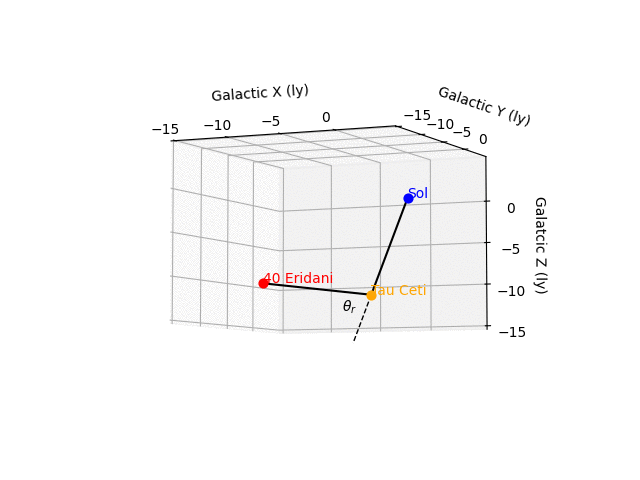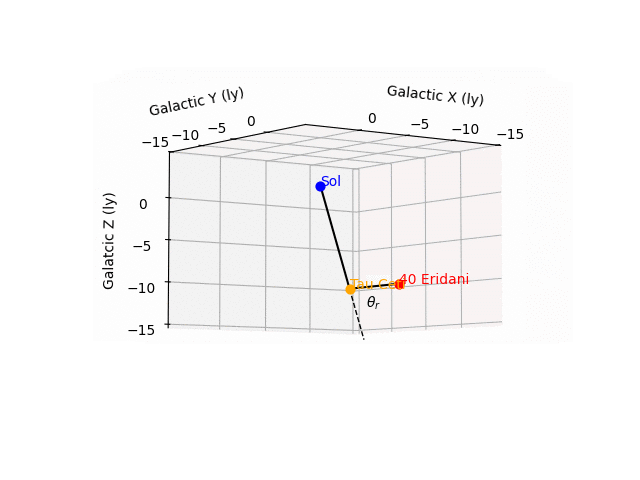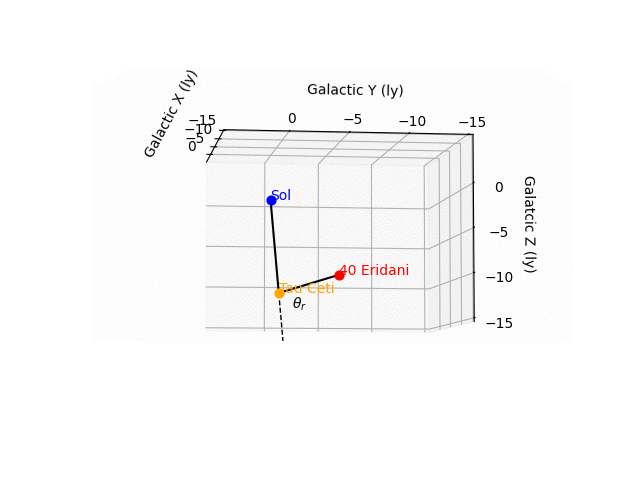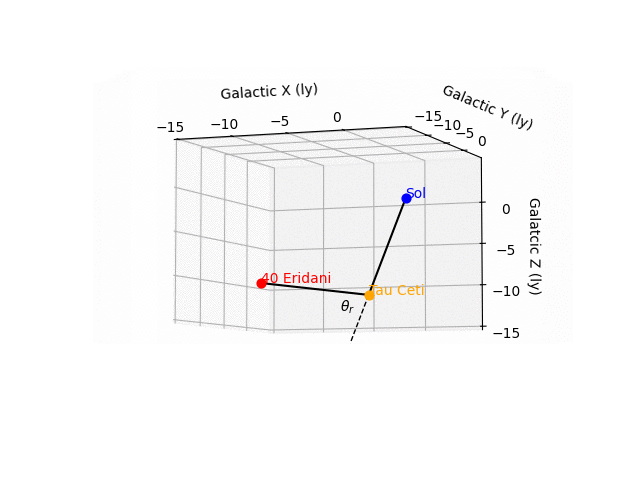
ワオ。クールだ。
ヘイル・メアリーの最高にクールな公式ミッションパッチ(サイン本といっしょに配布されたらしい)を思い出してしまう。もっとも、エリダニ40は当然ながら載ってないけど。
UK fans, join our virtual book tour on the 5th May for an exclusive UK and Ireland event. More info at https://t.co/bl2gAqQ6ja
— Andy Weir (@andyweirauthor) March 31, 2021
Special bonus: buy book with ticket and you can claim an exclusive Project Hail Mary mission patch. pic.twitter.com/2i6Cn4MdH3
ロッキーが主人公にくれた近隣の恒星の3次元模型も、がんばれば作れそうな気がしてくる(でも、ググったらとっくに3Dプリンタで作ってた人がいた)。
図をしげしげと眺めてみる。ソルからタウ・セチに向かう線とエリダニ40からタウ・セチに向かう線は直角に近い交わりかたをしている。図の中の $${\theta_r}$$ は 82.3 度だ(rがついているわけは後述する)。そしてエリダニ40からタウ・セチまでは9.700光年だとわかる。作中では10光年といっていたから、たしかに整合する。
オーケイ。これでぼくらは宇宙の地図を手にいれた!
これはおまけ情報だが、こちらには他の恒星も含めたもっと詳しい地図がある(2次元だけど)。タウ・セチ星系で生まれたアストロファージがどうやって太陽系やエリダニ40星系に伝播していったのかが推定されている。太陽系へは、意外と遠回りしているのがおもしろい。しかも、原作で言及されているWISE 0855-0714という天体が実は恒星じゃないらしく、それでもアストロファージは繁殖できるのか? なんて考察をしている。最高だ。
ヘイル・メアリーがタウ・セチに向かうと何年かかる?
では、地球からタウ・セチに加速度1.5Gでヘイル・メアリーが向かった場合、時間の遅れがどうなるのかを計算してみたい。
加速度 $${a}$$ で距離 $${d}$$ の天体に飛ぶ(中間地点で向きを反転して、$${-a}$$ で減速する)場合を考える。上記の特殊相対論のサイトによると、船内時間 $${t}$$、地球時間 $${T}$$、中間地点で到達する最高速度 $${v}$$ は、
$$
\displaystyle t = \frac{c}{a} \sinh{\frac{aT}{c}} = \sqrt{(d/c)^2 + 2d/a} \\
$$
$$
\displaystyle T = \frac{c}{a} \sinh^{-1}\frac{at}{c} = \frac{c}{a} \cosh^{-1} (ad/c^2 + 1) \\
$$
$$
\displaystyle v = c \tanh\frac{aT}{c} = \frac{at}{\sqrt{1 + (at/c)^2}}
$$
らしい(光速を $${c}$$ とする)。sinh とか cosh とか tanhっていうのは双曲線関数という、三角関数のいとこみたいなものだ。Excel とかにもふつうに入っている。Excel でも計算できる……そう考えると思ったほど難敵じゃない! もっと複雑な、意味不明の式が出てくるのかと思っていたので拍子抜けした。
これならぼくでも計算可能だ。いや、正確にいえば、計算するのはぼくじゃない。Excel だ。あるいは Python だ。「計算は手続き」。この数式の意味がまるでわからなくても、ただ手続きにしたがって値を代入すれば、答えが出るはずだ。
さあ、$${a}$$ に主人公が振り子で実測した加速度(1.532G)、$${d}$$ に 11.912光年を(SI単位系に換算して)代入してみよう。
その結果、こんな数字が出た。
船内時間 $${t}$$:3.84年(3年10ヶ月)
地球時間 $${T}$$:13.12年(13年1ヶ月)
最高速度 $${v}$$:0.995c
原作を見てみる。地球時間は13年、船内時間は約4年(3年9ヶ月)とある。
ワオ。
だいたい合ってる!
船内時間が1ヶ月ずれてるのは、もしかするとウィアーはきっかり11.9光年とかで計算してるのかもしれないし、加速度の計測誤差もあるかもしれない。
相対論の計算ってもっとややこしいのかと思ってただけに、こんなに簡単にウィアーとおなじ結果がえられたことにびっくりする。
オーケイ、この宇宙は計算できる! アンディ・ウィアーによって、そう作られている!
なんだか、プレイしていたゲームが物理演算エンジンで動いているのに気づいてしまった瞬間の感動に近い。でも、これはゲームじゃない。小説だ。おいおい、この小説は物理演算エンジンで動いているぞ!
ちなみに主人公は、加速度を0.9Gにすれば船内時間は5年半、ともいっていた。ついでにこれも計算してみよう。
船内時間 $${t}$$:5.52年(5年6ヶ月)
地球時間 $${T}$$:13.90年(13年11ヶ月)
最高速度 $${v}$$:0.988c
一致した! 相対論はすごい!
ブリップAがタウ・セチに向かうと何年かかる?
調子にのって、こんどはロッキーの船、ブリップAについても計算してみる。
ブリップAの加速度はあきらかになっていない。だけど、主人公はロッキーに「きみの船はぼくのより加速が大きい」といっていた。また、ロッキーの母星エリド(エリダニ40A b)の表面重力は地球の約2倍という記述が原作にあった。そこで、とりあえず2Gと仮定して計算してみる。
船内時間 $${t}$$:2.99年(2年12ヶ月)
地球時間 $${T}$$:10.62年(10年7ヶ月)
最高速度 $${v}$$:0.996c
主人公はロッキーに「きみは三地球年以内にエリドに着く」といっていた。だとすると、これはなかなかいい数字といえるんじゃないか?
ただ、ちょっと気になることがある。相対論を知らなかったロッキーたちはタウ・セチまで6.64年かかると思い込んでいた。しかし、だ。もし単純なニュートン力学 $${x=at^2/2}$$ での2Gの加減速を想定していたとすると、さっきの相対論のページにあった公式
$$
T' = 2 \sqrt{d/a}
$$
から、かれらが思い込む数字 $${T'}$$ は4.34年になるはずなのだ。たしかに相対論的経過時間の2.99年よりは長いけど、どうも合わない。どこから6.64年が出てきたのだろう? 加速度を0.85Gくらいに減らして再計算してみるとようやく6.64年になる。
まあエリディアンは寿命も長いし、人類よりは時間的に余裕がある。巡航中は動力を切って等速で飛ぶ想定だったのかもしれないな。旅路の最初と最後の9ヶ月を2Gの加減速にあてれば、ブリップAは光速の1.66倍(!)の巡航速度に達して6.64年程度で目的地に着く、と考えたのかもしれない。……うーん、無理があるか。もしなにか勘違いをしているようなら、教えてほしい。
ロッキーはどれほどめちゃくちゃな体験をしたのか?
それにしても、相対論を知らなかったロッキーたちは、さぞかし混乱しただろうな、と思う。一定加速度で加減速する宇宙船のわかりやすいアニメーションGIFが、ミズーリ大学セントルイス校(UMSL)のこのサイトにある。これを見ればロッキーの混乱をまさに追体験できる。
とりあえず2つ並んだ動画を見てほしい(下にスクショを載せるが、静止画では絶対伝わらないので、リンク先の動画を参照のこと)。

黄色い星から水色の星に小さな白い宇宙船が飛んで行く。左の動画は静止した慣性系(エリダニやタウ・セチ)の視点、右が宇宙船に乗ったロッキーの視点だと思ってほしい(細かい数値はちがうが、定性的にはおなじなので)。”turnabout"という表示はちょうど中間地点だ——船はここで反転して減速をはじめる。
右の動画では、常識では考えられないようなことが起こる。黄色いエリダニから出発したロッキーは、水色のタウ・セチがものすごい勢いで近づいてくるのにびっくりするだろう。予定よりずいぶん早く中間地点(turnabout)についたロッキーは船を反転させる。すると、どうだ。すぐに着くと思っていたタウ・セチがぜんぜん近づいてこなくなる。進んでも進んでもたどりつかない。
まさにそのようすを描写したのが、原作のこの部分だ。
「予定より早く中間地点に到達。ずっと早く。ぼくは船を反転させる。速度を落とすために推進。しかしタウ・セチは遠くなる。どうして?まだタウ・セチに向かって動いている、しかしタウ・セチが離れていく。とても混乱」
仲間が全員原因不明の病気(放射線障害)で死んでしまい、たった一人でこんな状況におかれたロッキーの困惑と焦りは察するにあまりある。
「ぼくは速度を上げる。下げる。大きな混乱。しかしここに着く。たくさんのまちがいと混乱があっても、ぼくはここに三年で着く。科学エリディアンがいう時間の半分。だからたくさん混乱」
さっきの動画を見たあとだと、もうこのあたりなんて涙なしには読めなくなってしまった。やっぱり相対論は、人類にもエリディアンにも直感的に理解しにくいみたいだ。
じゃあヘイル・メアリーがエリダニに向かうと何年かかる?
つぎは物語の終盤の旅路だ。主人公は結局ヘイル・メアリーでロッキーの故郷に行くことになった。これにはどのくらいの時間がかかるんだろう? とりあえず加速度は往路とおなじ1.532Gと仮定すると、
船内時間 $${t}$$:3.60年(3年7ヶ月)
地球時間 $${T}$$:10.89年(10年11ヶ月)
最高速度 $${v}$$:0.993c
になる。3年半もタウメーバを食べ続けたんだな……。ともかくこれで、主人公が経験した船内時間を見積もることができた。
これらの数字から推測されるライランド・グレースの年齢は?
オーケイ。必要な数字はそろった。それではいよいよ、主人公の年齢を見積もってみよう!
地球→タウ・セチ(船内):3年9ヶ月
タウ・セチ滞在期間:2ヶ月「二カ月間つきあった異星の知的生命体」
ロッキーと別れてから再会するまで:3ヶ月「別れてからほぼ三カ月」
タウ・セチ→エリド(船内):3年7ヶ月
エリドでの経過時間:16年+α「だがそれから一六年」
最終章(第
Vℓ章)での主人公の年齢:53歳くらい
そして、経過時間を全部足した23年9ヶ月を53歳から引く。
地球出発時点で29〜30歳くらい。タウ・セチでは32〜34歳くらい。
……ワオ。なかなかしっくりくる数字が出たんじゃないか?
念のため、地球側の経過時間も見積もってみる。
地球→タウ・セチ(慣性系):13年1ヶ月
タウ・セチ滞在期間:2ヶ月「二カ月間つきあった異星の知的生命体」
ロッキーと別れてから再会するまで:3ヶ月「別れてからほぼ三カ月」
タウ・セチ→エリド(慣性系):10年11ヶ月
エリドでの経過時間:16年+α「だがそれから一六年」
最終章(第
Vℓ章)における、主人公が生まれてからの地球の経過時間:71年
経過時間を全部足した40年5ヶ月を71年から引く。
地球出発時点で、ライランド・グレースが生まれてから約30年。
よい、よい、よい! 地球側の数字も整合している!
ちなみにヘイル・メアリーの建造期間は国際宇宙ステーション(ISS)の1/12だと書かれている。ISSは1998〜2011年までの13年間かかったらしい。となるとヘイル・メアリーは1年間で完成したってことになる。ストラット、とんでもないな。さらに建設のめどがたつ前には、主人公はアストロファージを培養するのに数ヶ月間を費やしているし、探査機アークライトが金星からアストロファージの入った試料を持ち帰るのにも三カ月かかっている(往路もそのくらいかかるのだろう)。なんだかんだで、物語の冒頭からヘイル・メアリーの打上げまでは1〜2年程度かかっていそうだ。
30歳前後。ちょうど博士課程を修了して、論文を書いてひどい目にあって、嫌気がさして教師に転職して数年、と考えると、なかなか説得力のある年齢が出てきたと思う。「つまりぼくは三〇代の独身で」という彼自身の推測ともぴったり合致する。
それでも不可解なアノマリーが残る?
……ところが、だ。どうしても整合しない箇所がじつはふたつあるんだ。
ひとつめは、物語の冒頭、記憶喪失になった主人公がはじめて地球での人生、マリッサとの食事を思い出すシーンだ。
ぼくらは二〇年近く前に大学院で出会った。
20年近く前に大学院だって!? どれほど優秀で飛び級を重ねていたとしても、たいていの大学院生は20代半ばだろう。仮に当時22歳だったとして、20年を足すとざっくり42歳。控えめに16年が経過したと考えても、38歳だ。アラフォーになってしまう。
百歩譲って彼が昏睡中の時間経過(3年9カ月)を把握していたとしても、まだ年数が足りない。いくらなんでも10代で大学院に行くような稀代の超天才としては彼は描かれていないように思う。
同じようなことを考える人はいるもので、Redditにスレッドが立っていた。
https://www.reddit.com/r/ProjectHailMary/comments/vhub03/how_old_is_ryland_grace/
ぼくとほぼおなじ計算によって30歳前後と結論づけている派閥と、マリッサの描写から40代と見なしている派閥にみごとに別れていて、ぼくとおなじように混乱している。
個人的には「記憶喪失なので適当な推測しかできてない」という説が気に入っている。いわゆる「信頼できない語り手」というやつだ。薬で無理やり記憶を消され、自分の名前すらわからなくなっている人間がようやく思い出した「20年前」という自己認識が、正しいとは限らないだろう? 任天堂パワーグローブのくだりも、決定的な証拠にはならないように思う。レトロゲーム機が好きな人間はアメリカにだってたくさんいる。
ちなみにこのRedditの記事で複数の人が「30代前半("early 30s")」という記載があったと書いているのだけど、そんな記載は日本語翻訳版にも原書にも見当たらない。ただ「三〇代(”in my thirties")」とあるだけだ。もしかして、初版以降で改訂されたんだろうか?
もうひとつのアノマリーは、さっきのに比べればささいなものだ。太陽の光度が復活したことを主人公が知る場面の記述についてだ。
ビートルズは地球に帰るのに12年かかるとされている(これはこのあと別の節でもふれる)。そして地球とエリダニ40のあいだは16.019光年。ビートルズが帰還後、一瞬で太陽光度が復活したとしても、その情報がエリドに届くには最短でも12+16=28年かかることになる。しかし、ヘイル・メアリーがビートルズを分離してから物語のラストシーンまでは、10年11カ月+16年+αで、およそ27年だ。
まあ、このくらいは誤差の範囲だろう。タウ・セチからエリドまでは、1.5G未満の加速で少し時間をかけて旅したのかもしれない。だって、ほら、いくら地球より近いとはいえ、ロッキーとロッキーの大量の荷物も積まないといけないし(さすがにブリップAを曳航するのは無理だろうな)。
それに、エリドでの「16年」は、当時は稚拙だったエリドのクローン技術を主人公が目の当たりにした時点が基点だ。おそらくエリドについてから、まともに彼が暮らせる環境が整うまで、1年くらいはかかったにちがいない。なにしろエリドは平均気温210℃の灼熱なのだ。いくらキセノナイトが優秀な断熱材だったとしても、並大抵のことじゃないだろう。
とはいえ、どちらにしても、やっぱりぼくがなにかをまちがえている可能性はあいかわらず非常に高いので、もし気づいたことがあればぜひ教えてほしい。
舞台はいったい西暦何年なのか?
ついでに、この作品の舞台がいったい何年なのかについてもちょっと考えてみたい。作中には、明確なヒントはない。ただ、少なくとも地球サイドについては、書籍(原著)が発行された2021年にかなり近い時代のように見える。登場人物はスマホやMicrosoft Excelを使うし、SpaceX社はすでに商用打上げを行っている。せいぜい10年以内の話だろう。
作中には「2017年のコンピュータ雑誌によると…」というくだりがある。だから、少なくとも2017年よりは後なんだろう。
ただ、これを公式情報と扱ってよいかは微妙だけど、アンディ・ウィアーは、PHMの(おそらく地球サイドの)各事象において、マーク・ワトニー(『火星の人』『オデッセイ』の主人公)はおそらく10代だろうと述べている(注意:仮定法で述べられているので、もし彼がいたら、というニュアンス。作品世界が共通かどうかは明言されていない)。
https://www.reddit.com/r/IAmA/comments/nkva3o/comment/gzf4276/
マーク・ワトニーは1994年10月12日生まれらしい(これが映画独自設定なのか原作もそうなのかはわからない)。もしこれがほんとうだとすると、PHMの地球サイドの話は2014年以前、ということになる。うーん、さすがにそれは時代が古すぎるんじゃないか、という気はする。
地球とエリドを行き来したらどうなるか?
これは、おまけの思考実験だ。エリドから主人公が帰ってきたり、逆に地球からエリドにだれかが行ったりしたらどうなるだろうか? 船はとりあえず、加速度はヘイル・メアリーと同じ仕様と仮定する。
船内時間 $${t}$$:4.20 年(4年2カ月)
地球時間 $${T}$$:17.56 年(17年7ヶ月)
最高速度 $${v}$$:0.997 c
オーケイ。船内時間は4年。地球での経過時間は17年半だ。
これなら、なんとか互いに行き来できそうな気がする。ぜひ、地球とエリドには交流を深めてほしいものだと思う。
ミンコフスキー図ってやつを描いてみるとどうなる?
ヘイル・メアリーのミンコフスキー図は?
相対論の話をググってるとやたらと「時空図」とか「ミンコフスキー図」ってやつを目にする。
時空図。ミンコフスキー図。ものすごく厨二病をくすぐられる、いや、クールな図だ。実は、なんのことはない。ものすごく乱暴な説明をすると、横軸が距離、縦軸が時間になっているグラフのことだ、と理解した(厳密な定義はここではおいておく)。難しいものじゃない。簡単なものなら、小学生だって意味を読み解けるだろう。
この図を描いてみたい。きっとすごくかっこいいにちがいない。
こちらのサイトなどを参考にして、ヘイル・メアリーの往路の船内時間1カ月ごとに、太陽系からの距離(光年)を横軸に、太陽系での経過時間(年)を縦軸に描いてみたのがこちらのグラフだ。なんかそれっぽい図が描けた! やったぜ!
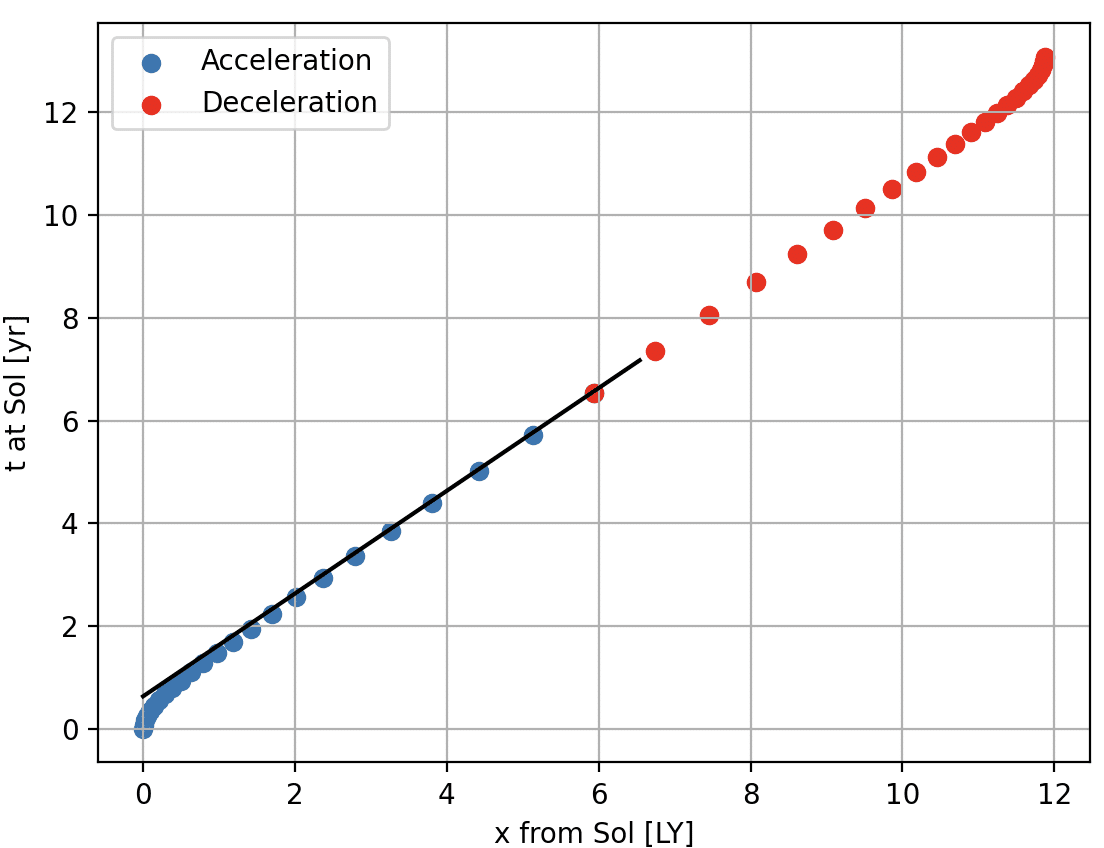
青点が加速フェーズ、赤点が減速フェーズだ。真ん中のあたりは点の間隔が開いていて、すごい勢いで空間も時間も過ぎ去ってるのがわかる。ちなみに船側の空間軸、時間軸も描こうと思ったけど、両者がローレンツ変換で傾いてほとんど重なってしまってわけがわからなくなるのでやめた(そのくらい光速に近い)。
黒い実線は青点が近づいていく漸近線で、光円錐を表している。つまりヘイル・メアリーは光の速度に近づいていく。ちなみに黒い実線と縦軸との交点は0.6年(7カ月)だ。これは、ヘイル・メアリーが出発して7カ月以上経ってしまったら、なにをどうがんばっても地球の情報は加速中のヘイル・メアリーには届かないってことを意味している。もっとも、後半になって減速すれば原理的には届くようになるけど、数年遅れで届いても意味がない。ヘイル・メアリーに地球と通信するためのアンテナがついていないのには、それもあるのだろう。なんとも潔い、無慈悲な特攻ミッションだ。
次のふたつの図は、速度がどう変化したかを地球時間と船内時間、それぞれで描いたものだ。
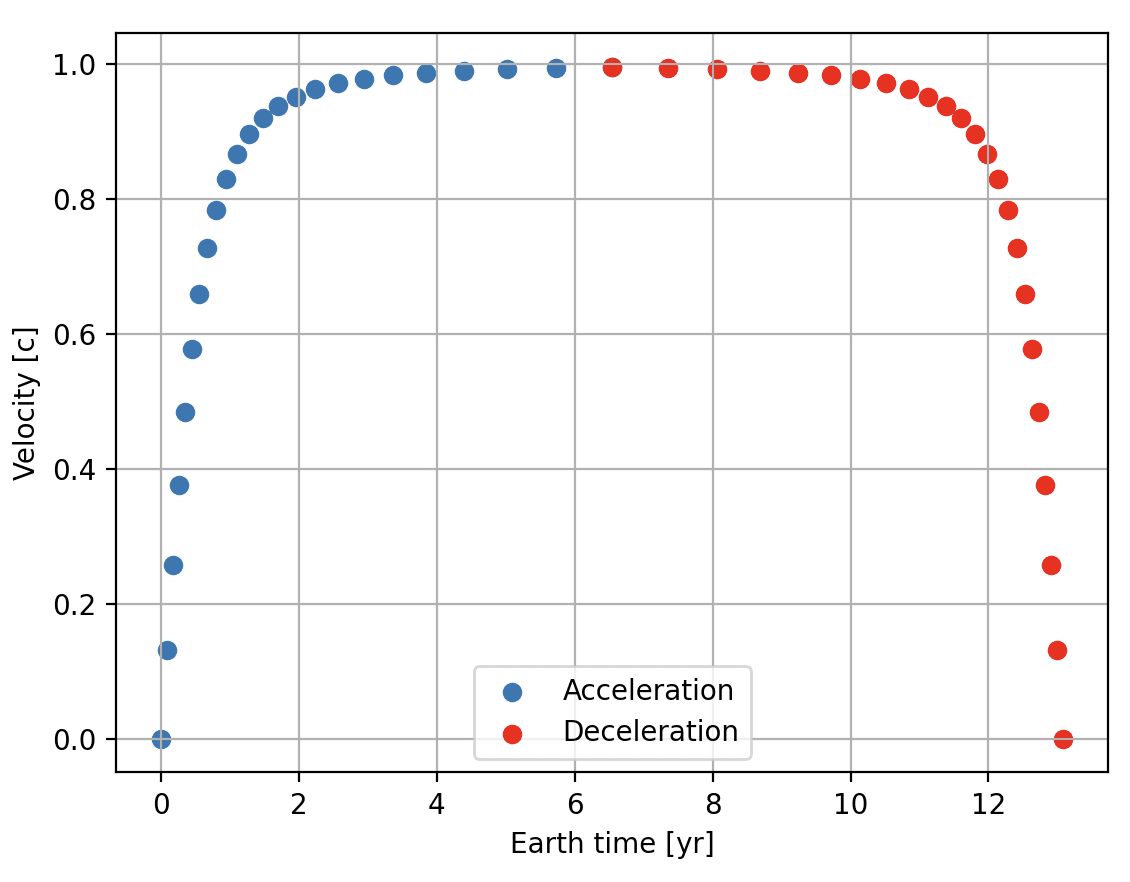
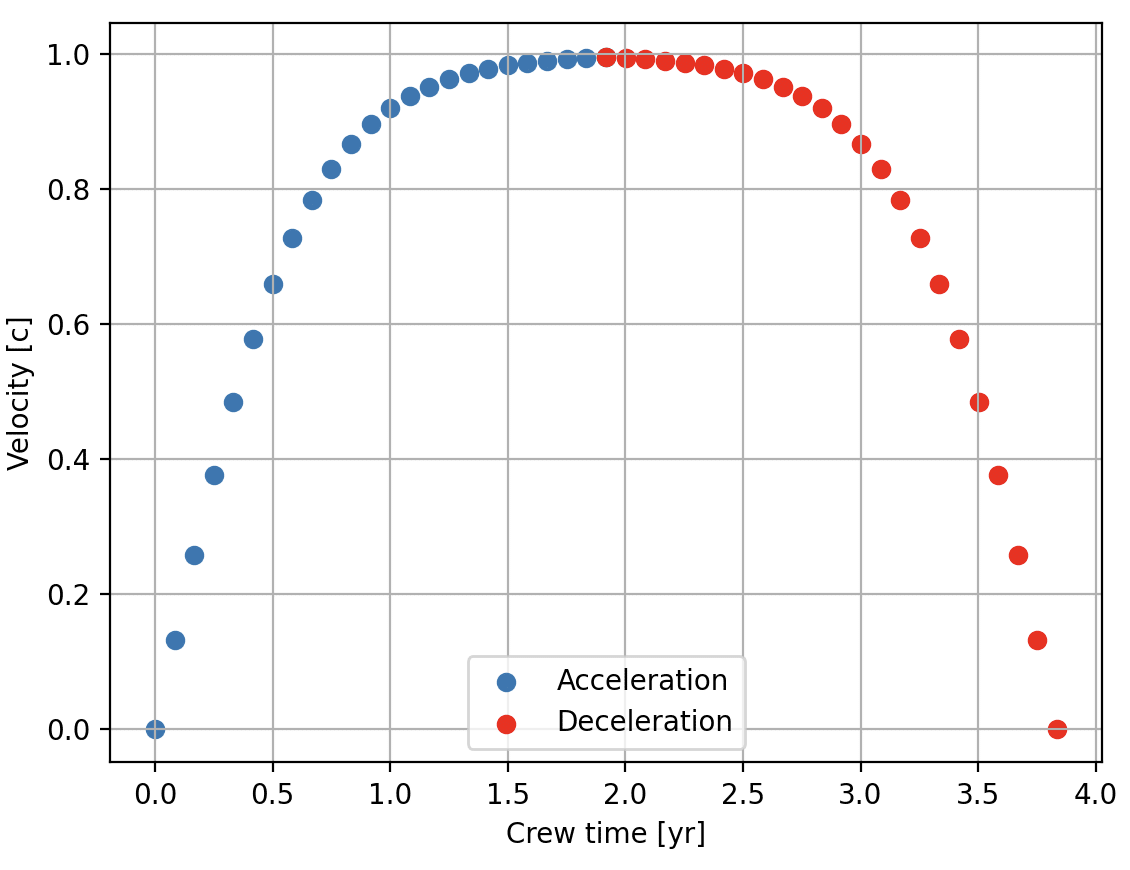
意外なことに、べつに出発後すぐに光速近くに達してしまうわけではないことがわかる。0.9cに達するのは地球でも船内でもだいたい1年後くらいだ。だから出発して最初の数カ月は、相対論的効果は非常に弱いはずだ。もっとも、互いの系を観測でもしないかぎり、相対論的効果を実感する機会はあまりなさそうだけど。たとえば船内から周囲の星空を見るとか、あるいは逆に地球からヘイル・メアリーを観測するとかでもしないと、わからないかもしれない。半年後くらいから、徐々に効果が現れるのだろう。
さらに次の図も見てみよう。ヘイル・メアリーの船内時間を横軸、地球時間を縦軸にとって、おなじく1カ月単位でプロットしたものだ。
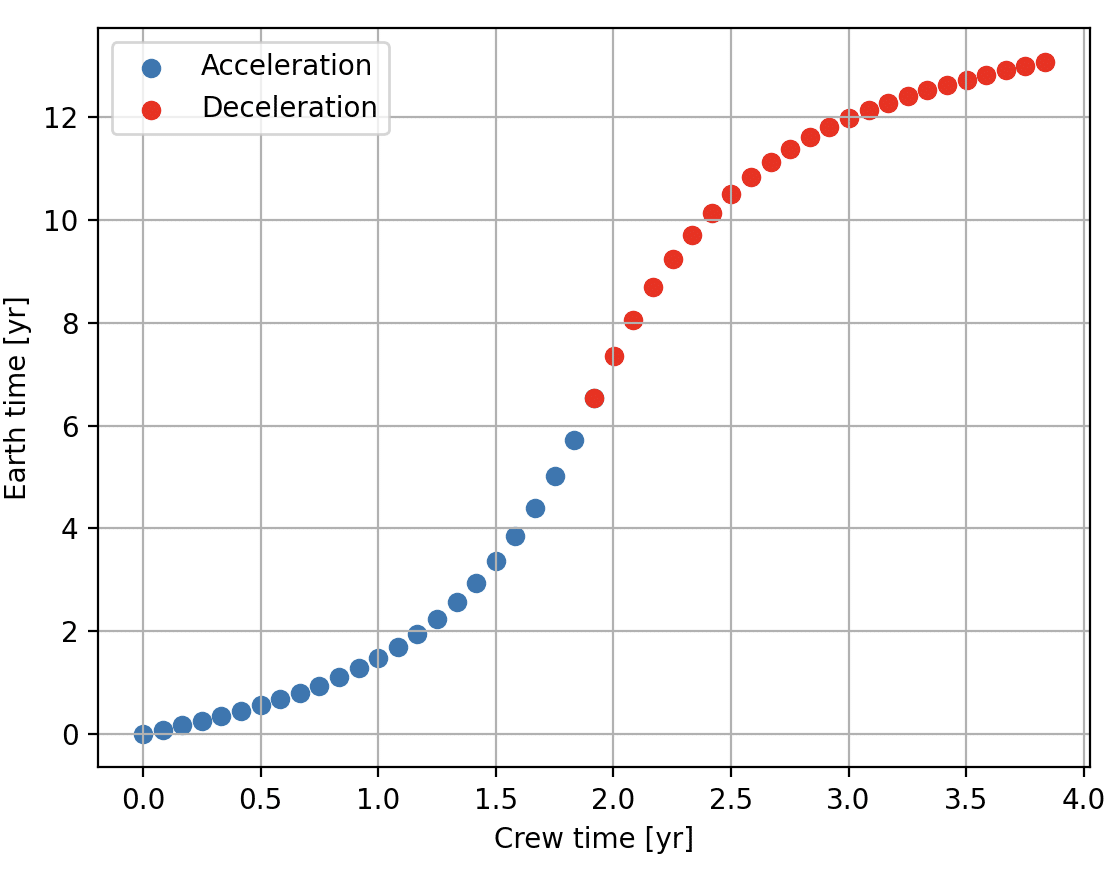
真ん中あたりの時間の進み方がすごいことがよくわかると思う。船内で3カ月(点3つ分)が経つあいだに、地球では2年が過ぎ去っている。意味がわからない。だけどおもしろい。
作中で、スティーヴ・ハッチといういかれたエンジニア(ビートルズを設計した人)がこんなことをいう場面がある。
神を信じます? 個人的な質問だってことはわかってるけど。ぼくは信じてるんですよ。で、〝彼〟は相対論をすごいものにしてくれたと思ってるんです。そう思いませんか? 速く進めば進むほど、経験する時間が少なくなる。まるで〝彼〟がぼくらに宇宙を探検しろといってるみたいじゃないですか、ねえ?
この台詞ひとつとっても、まったくいかれた野郎だと思うけど、個人的にはこのハッチと主人公の会話のくだりはけっこう好きだったりする。なにしろ今回、ぼくも相対論のことを調べるうちに「なんでこんなに宇宙は都合よくできてるんだ!?」って思ってしまったくちだ。1Gで加速すれば、アンドロメダ銀河へだって船内時間28年で行けてしまうのだから。——燃料問題さえなければ、の話だけど。なお、燃料については、このあとであらためて悩むことにする。
小説全体のミンコフスキー図はどうなる?
さっきの図は、地球からタウ・セチに向かったヘイル・メアリーのミンコフスキー図だった。同様に、物語の終盤でタウ・セチからエリダニ40に向かうヘイル・メアリー、そして地球に帰還するビートルズも含めて、ぜんぶひとつの図にしてみよう。
どうだろう? これが「全部入り」の図だ! 軌跡の始点や終点が微妙にずれているところがあるが、粗い計算のせいだ。許してほしい。
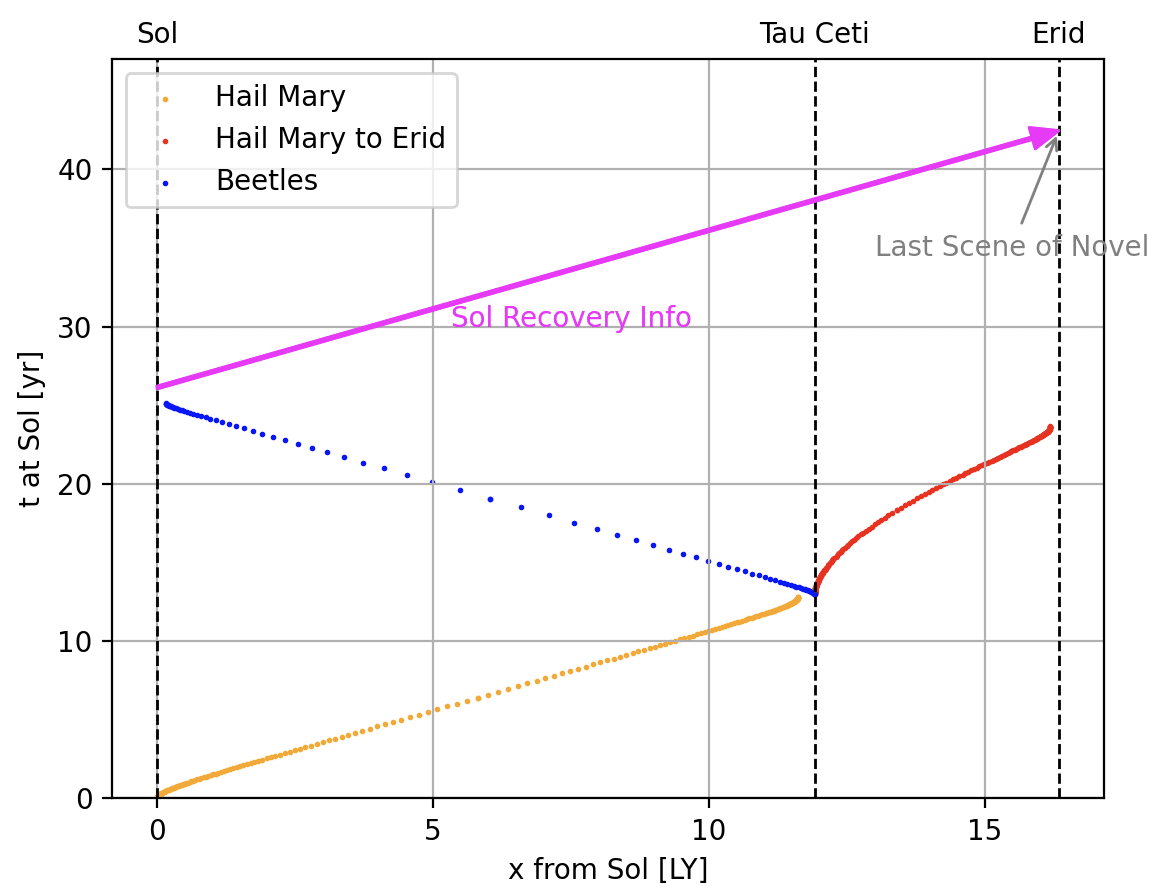
縦軸は、ヘイル・メアリーが地球を出発した時点からの地球での経過年数を示している。主人公の体験した年数ではない。
まず黄色い線を見てほしい。主人公は地球を出発して、12光年先のタウ・セチに到着する。地球時間では13年かかる。タウ・セチで2カ月ロッキーと一緒に奮闘したあと、ビートルズを分離して、ロッキーと一緒に40エリダニに行く。
青い線はビートルズだ。ここでは加速度4.8Gのケースを示しているが、500Gでもそんなに変わらない。ビートルズが地球に着くころ、地球では26年が経過している。
赤い線は、物語の終盤で40エリダニに向かうヘイル・メアリーだ。タウ・セチからエリダニまでは9.7光年だ(地球からは16.3光年)。地球時間で11年かかる。主人公はそのままエリドにとどまる。
さて、地球ではビートルズ帰還からおよそ1年で、太陽光度の復活に成功している。その情報は光としてエリドまで届く。それがマゼンタの矢印だ。光だから、単純に16.3年で伝わる。
マゼンタの矢印の先端で、主人公はソルの復活を知る。そう、ここが小説のラストシーンだ。エリドについてから約16年。地球側では40年ばかり経っている。さっきの計算結果とも整合する。
この図は、地球、タウ・セチ、エリド間のやりとりがいつ相手に届くかを考えるのに便利だ。基本的にあらゆる情報伝達は光速を超えない(超光速通信や航法を安易に導入せず、できるだけ既存の物理学の範疇でやりくりするのが、この作品の好きなところだ)。互いのやりとりをこのグラフ上に描くと、その傾きは必ず1以上になる。
たとえば主人公がエリドについて折り返し地球に連絡をしたとしよう。それが地球に届くのはビートルズ帰還から十数年後になる。地球からの連絡も同様だ。なかなかもどかしい意思疎通になるだろう。もはや、行ったほうが話が早いかもしれない。十数光年先まで飛んで行く技術はお互いすでに持っているのだし、直接会いに行く者にとってはたった数年の辛抱ですむんだから…。
燃料はほんとうに足りているのか?
質量比って何だ?
次は燃料のことを考えてみることにする。
ヘイル・メアリーは光速の99.5%まで加速する。もしかしたら、とんでもない量の燃料を積む必要があるんじゃないか? いったいどのくらいの量があれば、タウ・セチまで行けるんだろう?
燃料については、さっきの相対論のページ(知りたいことがほんとうになんでも書いてあってすごい)に、基本的な考え方が書いてある。
$$
M/m = \gamma (1 + v/c) - 1 = \exp(aT/c) - 1
$$
これは、質量 $${m}$$ の宇宙船本体を目的の速度 $${v}$$ まで加速するのに必要な燃料の質量 $${M}$$を表した式だ。宇宙船の質量と燃料の質量の比なので、質量比という。なお、$${\gamma}$$ っていうのは $${1/\sqrt{1-v^2/c^2}}$$ のことだ。ローレンツ因子というらしい。
たとえば質量比が10っていうことは、船本体の質量の10倍の燃料を積まなければならない、ということを意味する。船本体が100kgなら、燃料は1000kg必要っていうことになる。
さらに、この式はあくまで目的地をそのまま通り過ぎる場合の質量比であることに注意が必要だ。目的地で減速して止まる場合は、必要な燃料が全然違うよ、ということも、サイトに書いてある。たとえばもっとも近い恒星(たぶんケンタウルス座α星)に行く場合、通り過ぎるなら質量比は10だけど、現地で止まるなら38と書いてある。止まるにもエネルギーが要るのだ。
ヘイル・メアリーの質量比はいくつだろう?
では、これらをふまえてヘイル・メアリーの質量比を計算してみる。
中間点での最高速度:0.995c
質量比(最高速度に達するまで):19.796
質量比(タウ・セチを通り過ぎる場合):38.663
質量比(タウ・セチで止まる場合):431.470
タウ・セチで止まるには、船自体の質量の431倍もの燃料を積む必要がある、ということになる。
ところが、だ。
本文を見てみると、ヘイル・メアリーのペイロード(ドライ質量)は10万kg、アストロファージは200万kg と本文にある。つまり、質量比 20ってことだ。
うーん、おかしい。タウ・セチで止まるには燃料が少なすぎる。
20という数字は、最高速度 0.995c に達するまでの質量比 19.796 と奇妙に符合する。つまり、このままだと、中間地点で最高速度に達したところで燃料切れになってしまうはずだ。
じゃあ0.9Gで加速する場合はどうだろう?
主人公は 0.9G で地球に帰る場合の計算もしてくれている。検算のため、こちらも確認してみよう。
中間点での最高速度:0.988c
質量比(最高速度に達するまで):11.900
質量比(タウ・セチを通り過ぎる場合):23.092
質量比(タウ・セチで止まる場合):167.736
計算結果は168。
しかし、作中の計算では、燃料として 133万 kg を見積もっている。質量比 13.3 だ。やっぱり圧倒的に足りていない。しかも今回もなぜか、「最高速度に達するまでに必要な量」に近い数字になっている。
なにか計算がまちがっているのだろうか?
この資料にも「もし目的地での減速が必要なら、質量比は二乗しなければならない」と書いてある。たしかに目的地で止まる場合の数字は、最高速度に達するまでの数字のだいたい二乗くらいだ。
だいたい、ケンタウルス座α星に行く場合でさえ、質量比38だという。それより遠いタウ・セチに行くのに、質量比20でほんとうにいけるものなのだろうか……?
うーん、ほかのみんなはどう考えている?
困った。こういうときに必要なのは、先人の知恵だ。Redditをあさってみる。……やっぱり質量についての議論があった。ほんとうにRedditにはなんでもあるな!
https://www.reddit.com/r/printSF/comments/pr6fmu/spoiler_project_hail_mary_have_a_question_about/
そしてこんなすばらしい計算ページを見つけた(しかも2種類!)。どちらのサイトも、必要な値を入力すると、到着時間とか必要な燃料とか、そういったもろもろの値を計算して表示してくれるのだ。ありがたい!
このサイトでヘイル・メアリーについて計算してみると、どちらのサイトもやっぱりおなじ結果になった。巡航速度に達するための質量比は 19.79、目的地で止まるための質量比は 431.24 だ。
さらに探していくと、以下の2本のブログ記事を発見した。
うーん……。独立に書かれたこれらのブログもまた、ぼくとおなじ結果に到達していた。最初のブログがはじき出した質量比は415.6、次のブログも概算で400だ。20とかじゃない(ちなみに、2番目のブログはソーラーセイル推進なら質量比20で済む、と主張している。おもしろい。『太陽の簒奪者』だ! PHMファンにもお勧めの日本のSFだ)。
かれらはウィアーがまちがえたのではないか、「目的地で静止するための質量比」ではなく「最高速度に達するまでに必要な質量比」のほうを採用してしまったのではないか、と結論づけている。
たしかに、計算で出てくる数字は「最高速度に達するまでに必要な質量比」とほぼ一致している。
ほんとうだろうか。あれだけ緻密にすべてを計算するアンディ・ウィアーが、こんなところでまちがえるものだろうか。
ぼくはまだそう言い切れるだけの自信がない。「手続き」にしたがって意味もわからず計算したにすぎないからだ。だけど、400という数字をなにも考えず鵜呑みにするのも、なんだかちょっとなさけない。
オーケイ。うんと大雑把に、自分の頭で考えてみよう。
いったいどこから400という数字が出てくるのか?
ぱっと見では、加速フェーズと減速フェーズのちがいは、船が反対を向いているだけだ。船はただ中間点でひっくり返るだけでいい。中間点を挟んでちょうど対称な運動をしているように思える。だから一見、燃料は中間点まで加速するケースの2倍あれば充分な気がする。
だけど実は、加速フェーズと減速フェーズは対称ではない。最終的に残さなくてはいけない質量が圧倒的にちがうからだ。
時間的に逆算して考えてみる。つまり、長い旅の果てにタウ・セチに到着して静止した時点を起点として考えるのだ。
ヘイル・メアリーがタウ・セチで停止したとき、燃料をちょうど使い果たしたとする。このときの船全体の質量は10万kgだ(空っぽになった燃料タンクは一応投棄できるようになっているらしいが、いまは考えない)。つまり、最終的に10万kgが残るように燃料を積まなければならない。このとき、中間点での船の質量はどのくらいになるだろう?
中間点での船は、最高速度0.995cになっている。これを減速・静止させるというのは、速度0から0.995cまで加速するのとまったくおなじことになる。これを実現するための質量比は、さっき見たように 19.796 だ。ここではざっくり20としよう。つまり、中間点では、船の質量として10万×20=200万kgが必要になる。船体の95%が燃料ってことになる。
つぎに、中間点からさらにさかのぼって、出発時の質量を考えてみよう。速度0から0.995cまで加速するための質量比はやっぱり20だ。ここで注意しないといけないのは、今度は中間点を基点として考えないといけない、ということだ。さっき見たように、中間点での質量は200万kg。つまり、中間地点で200万kgが残るように出発地で燃料を積まなければならない。そのためには——出発時点で200万×20=4000万kgの質量がなければならない。燃料を運ぶための燃料が必要なのだ。
中間点から最終地点まで行くのに、20倍。それが出発点から中間点まで行くのに、さらに20倍。
だから、20×20=400倍もの燃料が必要になるのだ。
うん。たぶん。
正直、自信がない。合っているかわからない。
いや、正確には、これはこれで腑に落ちる。理屈は合う。ぼくだけならともかく、さっきのブログの書き手も含めて全員がなにか根本的にかんちがいをしている、とは考えにくい。
だけど、アンディ・ウィアーがなぜこの結論に至らなかったのか、がわからないのだ。こんな重要なところで計算まちがいをするだろうか? そもそも、彼にはたくさんの専門家がアドバイザーやベータリーダーとしてついているだろうに?
質量比400は「アンディ・ウィアー的宇宙」に似合わない?
うーん。ブログがいうように、アンディ・ウィアーはこの件を見落としたのだろうか。それとも彼は——あえて作劇のために大きな嘘をついたのだろうか。
もし仮に前者だったとしても、個人的にはこの作品の魅力が損なわれるものではないと感じる。こんな重箱の隅をつつくような計算をしてしまうほどにほかの部分のリアリティが高いということだし、この質量比が万が一まちがいだとしても、ものすごく惜しいところまで計算しているのはたしかなのだ!
そしてぼくは、後者の可能性——彼が意図的に質量比を20に抑えた、という可能性も、けっこうあるんじゃないかという気がしてきている。
すぐれたSFってやつは、なにかひとつの大きなハッタリをぶちかまして、その周囲をガチガチのロジックで固めることで、リアリティを高めるのが常套手段だ。本作でも、アストロファージやキセノナイトのいくつかの性質はあきらかに極上のハッタリだ(褒めている)。SF小説はエンタメであって論文じゃない。読者が気づかないところでいかにうまく嘘をついて、楽しさ・面白さをつくりだせるか、が作家の腕の見せどころなんだと思う。
考えてもみよう。船の質量比が400だったとする。その船が遠心モードになってぶん回ったり、船から船に乗り移ったり、エイドリアンの大気をかすめ飛んだり——あんなアクロバティックな活劇ができるだろうか? 少なくとも絵的に映えるだろうか?
ここで、人類がこれまでに実際に作り出した巨大な宇宙船のことを考えてみよう。たとえば、スペースシャトルの質量比は約16、アポロ計画に使われたサターンVロケットは23らしい(もちろん、推力自体はヘイル・メアリーのスピン・ドライヴとは桁違いに小さいので、恒星間航行ができるわけじゃないが)。つまり、ヘイル・メアリーの質量比20という数字は、ぼくらの知っているロケットにすごく近い。
さらに、じつはヘイル・メアリーはこれらのロケットよりかなり小さいのだ。

小説中の記載は全長47m。さらに縮尺が整合するようにファンが再計算して、ウィアーのお墨付きももらった数字が33m(詳しくは後で)。一方、サターンVの全長は110m、イーロン・マスクが開発中のスターシップとスーパーヘビーの組み合わせは120mもある。作中ではロッキーのブリップAが巨大な船として描かれていたけど、その大きさは140m。人類のロケットとたいして変わらない(ちなみにロケットエンジン部分だけ見ると、サターンVのF-1エンジンはヘイル・メアリーのスピン・ドライヴとほぼおなじ大きさなので、この記事のトップ画像にも使ってみた。ヘイル・メアリーの船体の妄想のお役に立てれば幸いだ)。
しかも、サターンVの太い部分がほぼ全部燃料であることを考えると、正直、ヘイル・メアリーの燃料ベイは小さすぎる気もする。まあ、もしかしたら満腹のアストロファージの比重はすごく大きいのかもしれない。ニュートリノがみっちり詰まっているらしいので。
ともかく、ヘイル・メアリーはほぼ既存の宇宙船のイメージに近いし、既存の技術でふつうに作れそうな気がしてくる。
じゃあ、質量比400の宇宙船はどうだろう——正直ぼくにはちょっと想像もつかない。見た目も思い浮かばないし、今のロケットの延長で作れる気がまるでしない。スペースオペラの宇宙船みたいな、オーバーテクノロジーじみた絵面がせいぜいだ。少なくとも扉絵のあの形状は無理だろう。つまり、質量比というリアリティを追求することで、かえって宇宙船自体のリアリティが薄まっていってしまうのだ!
これまでの作品を読むかぎり、こと宇宙開発に関しては、アンディ・ウィアーは徹底したリアリズムを貫こうとしているように思える。魔法と区別がつかないような、発達しすぎた科学技術は決して出さない。物理的かつ工学的に実現可能と読者の多くが思えるようなものしか登場させない。だからこそ、彼の宇宙に出てくるものはすべて計算可能なのだ。もちろん「そんなわけないだろう」的な部分も探せば出てくるが、毎回それらは実にうまく隠蔽されている。今回ぼくが無粋に指摘してしまった質量比問題も、そのひとつなのかもしれない。
なんとなくだけど、質量比400の宇宙船は彼の美学に合わないんじゃないか、とぼくはひそかに思っている。少なくともぼくらの技術レベルではあまりに非現実的だし、フィージビリティが「計算可能じゃない」からだ。もちろん、質量比20での恒星間航行もまた、一種のリアリティの破壊だ。だけど、そこの筋を通そうとすると、他のリアリティが大幅に犠牲になる。ウィアーはどう見てもかなりの宇宙開発マニアなので、そこのディテールは死守したかったのかもしれない。もしアンディ・ウィアーの作品に質量比400の宇宙船が出てきたら、ぼくだったらちょっぴり興醒めしてしまうんじゃないかと思う(ちなみに、ダイダロス計画でさえ質量比100だ)。ちなみにブリップAはキセノナイトのおかげでかなり非現実的な形状をしているけど、ウィアーは頑なに船内の描写を避けている。計算可能でないものを「描写しようがない」からだ。
そして、『火星の人』の映画化をすでに経験したアンディ・ウィアーは、おそらく本作については最初から映像化を見越して書いているんじゃないかという気がする。実際に、そう思わせるようなシーンもいくつかある。明らかに『火星の人』よりもさらに映像喚起力が高い仕上がりになっているからだ(どう映像化するのか見当もつかない部分も多々あるけど)。そのうえでも、ヘイル・メアリーを「既存のロケットの延長線上にある宇宙船」として描きたかったのかもしれない。
それでもやっぱり科学的正確性こそがウィアーの要なんじゃないか?
……とまあ、自分自身を言い聞かせようとしたわけだが、ここまで書いておいてなんだけど、ぼくはまだどうしても完全に納得できていない。たしかに質量比400の宇宙船は非現実的だ。だけど、果たしてウィアーはそのために物理法則をねじ曲げるだろうか?
アンディ・ウィアーの『火星の人』時代のインタビューをいくつか読んでみたのだが(どれもほんとうに良い記事でおすすめだ)、創作に対する彼の姿勢は首尾一貫している。
I guess I just really enjoy the process of learning new things. I love doing research. When I’m writing my stories, I try to be as scientifically accurate as possible. And that’s the really fun part for me is researching and the problem solving.
(筆者訳:ぼくは本当に新しいことを学ぶプロセスが好きなんだと思います。リサーチが大好きなんです。ストーリーを書くときには、できるだけ科学的に正確になるように努めています。リサーチや問題解決はぼくにとって本当に楽しい部分です)
All that science was as technically accurate as possible, helped by feedback from Weir’s mailing list.
“I wanted to make sure that geeks like me could enjoy the book, so I put a huge amount of effort into making sure it was scientifically accurate,” he says.
(筆者訳:あらゆる科学はウィアーのメーリングリストからのフィードバックのおかげで、可能な限り技術的に正確だった。「ぼくみたいなオタクが確実に本を楽しめるようにしたかったんです。だから科学的に正確を期することを確かめるのにものすごい労力を費やしました」とウィアーは語る。)
ウィアーは科学的正確性をほんとうに大事にしている。もちろん、あらゆるSF作家は科学をないがしろにしないが、ふつうは科学的正確性の確認をこっそりやっている。あからさまに作品に書かない。でも、ウィアーはちがう。多くの計算過程をオープンにして読者がたどれるようにしている。そのプロセスがほんとうに楽しいものであることを熟知しているからこそ、読者にもその楽しみを惜しげもなく共有してくれているのだ。その甲斐あって、彼のメーリングリストの3000人のメンバーからは積極的にフィードバックが寄せられるし、ウィアーの予想どおり、ぼくみたいなオタクがまんまと引っかかってこんな記事を書いているわけだ。
そのウィアーがこんなところで妥協するとは、やっぱり思えないのだ。ましてや、3000人のコアなファンもだまっていないと思う。
うん。かなりのひいき目であることは認める。だが、ぼくはまだ、質量比20での恒星間航行を可能にする合理的な解がどこかにあるのでは、という考えに一縷の望みを抱いている。根本的になにかを自分が見落としているのかもしれない。そうであってほしい。今後もその可能性を追求しつづけたいと思う。
だから、もし上記の議論でなにか気になる点を見つけた場合は、どうかぜひ教えていただきたい——ぼくが自分だけで楽しまないでわざわざこんな記事を書いて意見を募っているのも、きっと科学ってそういうものだからだ。ぼくだけでは手詰まりなのだ。どうか、協力をお願いしたい。
ビートルズの加速はクレイジーすぎないか?
さて、ビートルズだ。
500Gという、クレイジーな加速度で太陽系に向かって打ち出されるジョン、ポール、ジョージ、リンゴ。どんなクレイジーな計算結果が出てくるのだろうか。
ビートルズの諸元はこちらだ。
〇・九三c(cは光速を表す記号)の巡航速度に達するまで五〇〇Gで加速してね。地球にもどるのに一二年以上かかるけど、最終的にそいつらが経験するのはたった二〇カ月で。
加速度500Gを入力して、同様に計算してみよう。
加速度 $${a}$$:500G
船内時間 $${t}$$:0.03年(12.35日)
地球時間 $${T}$$:11.92年(11年11ヶ月)
最高速度 $${v}$$:0.99999995 c
質量比(最高速度に達するまで):6149
質量比(太陽系で止まる場合):37825480
いやいやいや、待ってくれ。地球まで12日って。20カ月かかるはずだろう?!
そういえば巡航速度0.93c と書いてあった。この速度に達したらあとは一定速度で飛ぶのかもしれない。加速→巡航(0.93c)→減速、というプロファイルで考えてみる。
加速度 $${a}$$:500G
船内時間 $${t}$$:4.71年(4年9カ月、加減速にそれぞれ1.79日)
地球時間 $${T}$$:12.81年(12年10ヶ月)
最高速度 $${v}$$:0.93 c
質量比(最高速度に達するまで):Inf
質量比(太陽系で止まる場合):Inf
おいおい、今度は時間がかかりすぎだ! しかも質量比が Inf になってしまった。ぼくの Python もお手上げだ。——うん。まあ、質量比のことはいったん置いておこう。こんどは巡航速度をもう少し上げてみよう。たとえば、0.99cとか。どうだろう?
加速度 $${a}$$:500G
船内時間 $${t}$$:1.70年(1年8カ月、加減速にそれぞれ4.97日)
地球時間 $${T}$$:12.04年(12年0ヶ月)
最高速度 $${v}$$:0.99 c
質量比(最高速度に達するまで):1.024e+191
質量比(太陽系で止まる場合):Inf
ビンゴだ! ちょうど20カ月と出た! ……とはいえ、相変わらず質量比はふざけた値を示している。ここで、1.024e+191というのは、$${1.024 \times 10^{191}}$$ ってことだ。めちゃくちゃ巨大な数やうんと小さい数を表すのに、ゼロを191個も書く気がしないので、こういう便利な表記(指数表記)を使っている——たとえば1億円は1e8($${1 \times 10^{8}}$$)円、0.0000001 グラムは1e-7 ($${1 \times 10^{-7}}$$)グラムだ。話を戻すと、観測可能な宇宙の質量が 1e53 kg のオーダーなので、もはや宇宙のすべての質量をかきあつめてもビートルズにこの加速度は出せない。
ちなみに、500Gなんていわず 4.8Gくらいの加速にしておけば、わりと常識的な質量で、しかも20カ月で地球につく。これなら、本体を数ポンドといわず30g程度のラズパイかなんかで作っておけば、アストロファージ125kgでなんとかなるだろう。もっとも、物語の途中で主人公が重量1kgのタウメーバ農場を後付けで載せてしまったから、このままではスペックアウトだ。125kgの燃料でまかなうには、4.8Gからさらに加速度を減らす必要があるかもしれない。
加速度 $${a}$$:4.8G
船内時間 $${t}$$:1.66年(1年8カ月)
地球時間 $${T}$$:12.31年(12年4ヶ月)
最高速度 $${v}$$:0.9995 c
質量比(最高速度に達するまで):60
質量比(太陽系で止まる場合):3720
いったいどこから500Gとか0.93cという数字が出てきたのかは結局よくわからないが、もしかしたら純粋な加速度ではなくて、分離時の衝撃とか機体の振動とかいった一時的な加速度なのかもしれない。まあ、ビートルズについては、これ以上有益な情報が得られそうにないので、ここでやめておく。
で、例によって Reddit を見たらやっぱり議論されていた。0.93c は平均速度なんじゃないか? っていう意見があったりして、なかなかおもしろい。
ペトロヴァ波長はなぜ26ミクロンなのか?
さて、つぎは相対論から少し離れて、PHMに出てくるふたつの印象的な数字について考えてみたい。
25.984 μm。
96.415 ℃。
言わずと知れた、ペトロヴァ波長とアストロファージの温度だ。
作中ではこれらの数字が何度も何度も出てくる。本作を特徴づける値といっていい。アンディ・ウィアーが適当に設定したのだろうか? それにしては、やけに細かい。具体的すぎる。
あやしい。ものすごくあやしい。
推理小説に出てくる、使用人の証言とかあからさまなアリバイみたいなものだ。アンディ・ウィアーはこの値を、計算によって導き出した。そんな気がしてならない。
うん。計算せずにはいられない。
ペトロヴァ光の波長はニュートリノの質量で決まる?
ペトロヴァ光の波長は、25.984 μm だという。ロシアのプルコヴォ天文台のペトロヴァ博士が発見したから、ペトロヴァ光だ。
アストロファージが0.92cで移動するときに発せられる波長だ。厳密にいうと、金星と太陽をそんな猛スピードで往復してるのならドップラー効果で波長が変化しそうなものだが(実際、作中ではインド宇宙研究機関がそれを発見していたが)、ペトロヴァ博士は「すべておなじ波長」といっていたので、そのへんの偏移は除去したうえでの数字なのだろうと解釈する。
たとえば、この波長、25.984 μm をぼくらが知らないと仮定して、他の数字から導き出すことができるだろうか? チャレンジしてみたいと思う。
物語の中盤では、ロッケン博士によって、ペトロヴァ光は「アストロファージがニュートリノの質量をエネルギーに転換するときに発生する」ことが明かされた。アストロファージは逆に「周囲の熱エネルギーをニュートリノに変える」こともできる。かれらは物質をエネルギーに変換したり(対消滅)、エネルギーから物質を生み出したり(対生成)、ということが自在にできる。アインシュタインの $${E=mc^2}$$ を日々実践しているのだ。まったくとんでもないやつらだ。
つまり、ニュートリノの質量を $${m_{\nu}}$$ とすると、発生する光のエネルギー $${E}$$ は$${m_{\nu}c^2}$$ になる。エネルギーがわかれば光の波長もわかる。オーケイ。簡単だ!
だけど、ひとつ落とし穴がある。
残念なことに、ぼくら人類は、ニュートリノの質量を正確には知らない。少なくともいまのところは。まあ、アンディ・ウィアーのニュートリノまわりのアドバイザーはCharles Duba博士という専門家らしいので(しかも高校の友人らしい)、それらしい数字を持ってるのかもしれないが、直接の描写はされていない。
たとえばここを見ると、人類は3種類のニュートリノの合計の「上限値」しか推定できていない、とわかる。しかも諸説ある。上限値がざっくり 1.7e−37 kg (0.1 eV)くらいらしい、ということがわかっているだけだ。
ところが、だ。ロッケン博士たちはどうやらニュートリノの質量を知っているらしい。「陽子の200億分の1程度」だと言っている。仮にきっかり 200 億分の1だとすると、8.36e-38 kg になる。
ずいぶんアバウトな推定値ではあるが、この値をそのまま使ってしまおうか?
——いや、待てよ。ニュートリノが関わる反応が、作中にもうひとつある。
アストロファージの体内で起こる「ニュートリノの対生成」だ。陽子と陽子が衝突してニュートリノが対生成するらしい。
アストロファージは陽子同士を衝突させて一対のニュートリノをつくる。その反応を生じさせるには、陽子同士は、ニュートリノ二個の質量エネルギーより大きい運動エネルギーで衝突する必要がある。ニュートリノの質量から逆算すれば、陽子同士がどれくらいの速度で衝突しなければならないかがわかる。そしてその物体のなかの粒子の速度がわかれば、その温度がわかる。ニュートリノをつくれるだけの運動エネルギーを持つためには、陽子は摂氏九六・四一五度でなければならない。
彼女がいうように、ニュートリノの質量とアストロファージの温度は密接に結びついている。そして、アストロファージの温度はかなり精密にわかっている。そう、96.415 ℃だ。この温度の値を使えば、ニュートリノの質量がかなり精度良く求まるんじゃないか!?
よし、ロッケン博士たちとはまったく逆のアプローチを取ってみるとしよう。アストロファージの温度からニュートリノの質量を求めてみるのだ!
アストロファージの温度から陽子の速度を求めると?
アストロファージの中では、陽子と陽子がすごい勢いでぶつかって、一対のニュートリノができる。陽子が持っていた運動エネルギーがニュートリノのペアに変換されるのだ。だからまず、陽子の運動エネルギーがどのくらいだったのかを考えないといけない。そしてそれは温度だけで決まるのだ。
温度は、分子や原子の運動エネルギーそのものだ。温度が高いほど、原子や分子はスピードアップする。ざっくりいうと、陽子の絶対温度 $${T}$$ がわかれば、以下の式から平均速度 $${v}$$ がわかる。たぶん。$${m_p}$$ は陽子の質量、$${k_B}$$ はボルツマン定数という決まった値だ。
$$
\displaystyle \frac{1}{2} m_p v^2 = \frac{3}{2} k_B T
$$
ここにアストロファージの温度 96.415℃(絶対温度だと369.565 K)を入力すると、陽子の速度は 3025 m/s だとわかる。秒速3キロ。たとえば極超音速機 X-15 の最高速度は 2 km/s だ。
陽子の速度からニュートリノの質量を求めると?
さて、3025 m/s で互いに逆方向から進んできた陽子と陽子が正面衝突したとしよう。このときの運動エネルギーがすべて一対のニュートリノに変換されるとする。一対の、というのはニュートリノと反ニュートリノのペア、という意味だ。ロッケン博士によるとニュートリノはマヨラナ粒子——粒子と反粒子がおなじもの——らしいので、両者の質量もおなじ $${m_\nu}$$ だと思っていいだろう。
$$
\displaystyle \frac{1}{2} m_p v^2 + \frac{1}{2} m_p v^2 = m_\nu c^2 + m_{{\nu}}c^2
$$
ここから、ニュートリノ質量 $${m_\nu}$$ は 8.516e-38 kg (0.0478 eV)とわかる。陽子質量の 196 億倍だ。たしかにロッケン博士のいったとおりだ。
ニュートリノの質量からペトロヴァ波長が得られるだろうか?
これで、ようやくニュートリノの質量を求めることができた。もちろん、あくまでPHM世界における値だ。さあ、ゴールはもうすぐだ!
アストロファージは、一対のニュートリノを対消滅させてエネルギーに戻すことができる。出会ったら最後、文字通り一触即発のニュートリノのペアを、ふだんどうやって対消滅させずに体内に保存しているのかさっぱりわからないが、ともかく好きなタイミングで器用にペアをぶつけて光に戻しているのだ。
そう。ニュートリノの質量エネルギーはペトロヴァ波長の光の光子一個が持つエネルギーとぴったり一致するの。
ニュートリノの質量エネルギーが波長 $${\lambda}$$ の光子1個のエネルギーと等しい、ということを式にするとこうなる。 $${h}$$ はプランク定数という決まった値だ。
$$
E = m_\nu c^2 = hc/\lambda
$$
ここから波長 $${\lambda}$$ を求めてみると…
25.954 μm。
ワオ。
ほぼペトロヴァ波長だ! ほんとうにペトロヴァ波長が出てきた!
つくづく感心する。ウィアーの作り込みはほんとうに半端ない。
おそらく、PHMを執筆するうえで最初に決まったのは、ニュートリノの質量なのだろう。この値さえ決めてしまえば、そこからペトロヴァ波長もアストロファージの温度も決まってしまう。決してアンディ・ウィアーが適当においた数字なんかじゃない。徹底した計算可能な宇宙だ。
とはいえ、実に絶妙な数字を設定したものだと思う。
もしペトロヴァ波長がガンマ線やX線だったら——人体への影響が大きすぎる。その設定でのプロットはあまり想像したくはない。25.984 μm は、目には見えず、だけど赤外線ゴーグルなら見える、じつに扱いやすい波長だ。
アストロファージの温度も、人間がなんとか扱える程度であって、かつ水が沸騰しないぎりぎりの——おっと、水が100℃で沸騰するのはあくまで1気圧の条件においてだ。高い山の上ではもっと低い温度でお湯が沸く。ましてアストロファージがいるのは宇宙だ……
あれっ。ということは、アストロファージの細胞内は、常に1気圧以上を保っているのだろうか? 真空中でも? アストロファージの故郷と推測されるエイドリアンもべつに高圧の世界じゃない。せいぜい0.02気圧だ。
なぜアストロファージは、宇宙空間でも、地球やエリドの大気圧下でも、破裂したり押しつぶされたりしないのだろう。細胞膜がよほど頑丈なのだろうか? 科学的な棒で科学的に突っついたら破れるのに? タウメーバも、そんなパンパンのゴム風船のようなアストロファージを真空中で食べたとたんに、破裂に巻き込まれて死んでしまわないのだろうか。それともなにか、細胞内の水を液体に保つ未知の機構が存在する?
……うーん、これ以上はわからない。情報がなさすぎる。だけど、まあ、基本的な物理定数だけからこれらの設定が導き出せてしまう。それほどの世界の作り込みは、まったくたいしたものだと思う。
スピン・ドライヴの噴射光はどれほど遠くまで届くのか?
これは完全に与太話だけど、ヘイル・メアリーのスピン・ドライヴから出る噴射光についても、ちょっと考えてみたい。
スピン・ドライヴはペトロヴァ光を噴射する。遠赤外線だ。目には見えない。適度な強度なら当たったらポカポカとあたたかそうだし、焼き芋だって焼けるかもしれない。
しかしスピン・ドライヴから発せられるペトロヴァ光は、200万kgの宇宙船をタウ・セチに放り投げられるくらいのおそろしいエネルギー量をもつ。おおよそ人類が扱ったことのないような規模のエネルギーだ。作中でもわずかなアストロファージから出る光でシリコンの塊が溶けたり、大事故が起こったりしていた。
そんなに強烈な光だとしたら——もしかして、すごく遠くからでも見えるんじゃないか? もちろん、目には見えないだろうけど、たとえば遠赤外線を捉えられるカメラやサーモグラフィ、赤外線用の望遠鏡とかなら。
たとえば、タウ・セチにいるヘイル・メアリーの光やブリップAの光も、がんばれば太陽系から見えたりするんじゃないだろうか!?
どういうわけか、そんな考えにとりつかれてしまったぼくは、計算してみることにした。
ドップラー効果でペトロヴァ光の色はどんなふうになる?
本作に出てくる船は、基本的にどれも光速に近いスピードで飛んでいる。すると、常識では考えられないようなことがいくつも起こるらしい。
まずは、光の波長、つまり色が変わる。いわゆる、ドップラー効果だ。
もちろん、ドップラー効果自体は光速に近くなくても起こる。ぼくらも日常的に経験している、救急車のサイレンの音が高く聞こえたり低く聞こえたりするあれだ。
船が近づいてくるときは波長が短くなって青い側にズレるし(青方偏移)、遠ざかるときは波長が長くなって赤い側にズレる(赤方偏移)。だから、船のスピードが増すと、スピン・ドライヴから出るペトロヴァ光は、もはやペトロヴァ周波数ではなくなってしまっていることになる。
さらに、亜光速特有の現象もある。船が近づいても遠ざかってもいない、ただ目の前を横方向に通り過ぎるときでさえ、光速近辺ではドップラー効果が現れる。横ドップラー効果とかいうらしい。
たとえば太陽系から見ると、タウ・セチからエリダニ40に向かうベクトルは、$${\theta_r}$$ = 82.3度傾いている。つまり、物語の終盤でエリダニ40に向かうことにしたヘイル・メアリーを地球から見ると、ほぼ真横に進んでいるように見える。

日常の感覚だと、物体が目の前を真横に通り過ぎるだけであれば、ほとんどドップラー効果は現れないように思える。だけど光速に近づくにつれ、横方向の移動であってもドップラー効果が生じる。それが「横ドップラー効果」だ。初めて知ったよ。
じゃあ、どんな波長になるのだろう? ググったところによると、ヘイル・メアリーが太陽系から見て角度 $${\theta_r}$$ だけ傾いた方向に光速の $${\beta}$$ 倍の速度で進んでいるとき、周波数 $${f_s}$$ で光源から出た光の周波数は
$$
\displaystyle f_r = \frac{f_s}{\gamma(1+\beta \cos \theta_r)}
$$
になるらしい。$${\theta_r}$$ が 0 度というのはまっすぐ遠ざかっているケース、180度というのはこっちに向かってきているケースに相当する(sはsource、rはreceiverの意味でつけた)。
この式は、通常のドップラー効果と横ドップラー効果をまとめてひとつの式で表したものになっている。これを使って、実際に波長を計算してみたのが次のグラフだ。横軸は船の速度(光速に対する比率)、縦軸はペトロヴァ光の波長だ。
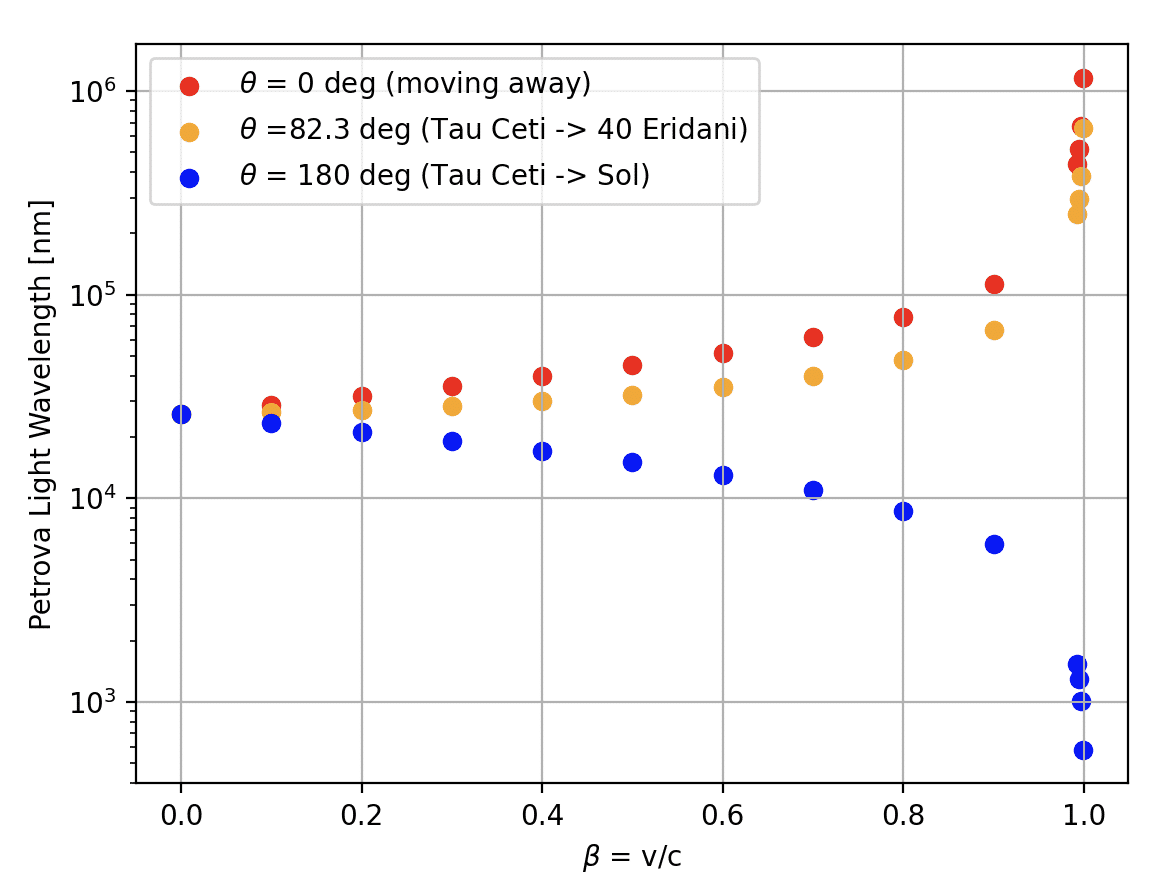
赤は、船が地球からまっすぐ遠ざかっているケース。地球から出発したあとのヘイル・メアリーがこれにあたる。船が加速するにつれて光の波長は遠赤外線を超えてマイクロ波とかサブミリ波などの電波に近くなっていく。
青は、船が地球にまっすぐ近づいてくるケース。地球に帰ってくるビートルズはこれだ、0.999cの場合、581nm。もはや可視光の波長になっている。つまり、帰ってくるビートルズの光は人の目で見える波長にまで達するってことだ! もっとも、最高速度を出しているときはまだかなり遠いはずなので、肉眼ではきびしいだろうが。
オレンジは、82.3度の角度で横向きに進んでいるケース。ちょうど、タウ・セチからエリダニ40に向かうヘイル・メアリーを太陽系から見ている場合に相当する。横向きにしては、意外と赤方偏移が大きいことがわかる。少なくとも、ペトロヴァ波長からは少しずれた波長になる。
横に進んでいるのに、船の後ろ側がなぜか見えてしまう?
でも、待てよ。真横に進んでいるのなら、船尾のスピン・ドライヴは見えないのでは? ちょうど、目の前を通り過ぎる車のテールランプが見えないのとおなじように——最初、ぼくは単純に、そう思った。
ところが、調べていくうちにぼくはさらに驚愕の事実を知った。専門用語ではテレル回転というらしいが、まあそれはどうでもいい。光速に近い速度で真横に進んでいる物体を見ると——なんと、後ろ側がこっちに向いて見えるらしいのだ!

知らなかった。ぼくはほんとうにびっくりしてしまった。本来は見えないはずの面、車であればテールランプ、宇宙船であれば船尾が見えるらしい。そんなばかな、と思ってしまうが、どうもそうらしい。ちなみに、実際に船が回転しているわけではなくて、あくまで見かけ上そう見える、というだけだ。
これらの一見奇妙な現象を楽しく遊びながら体験できるシミュレーションが京都大学の講義サイトにある。
目の前を電車が横切る、何の変哲もない風景だ。ところが電車の速度が光速に近づいていくと、なんと電車の末尾が見えてくるのだ! Cボタンでドップラー効果による色の変化をオンにすれば、赤方偏移や青方偏移(横ドップラー効果も含め)により色が変わるようすもわかるかと思う。

ちなみにこのシミュレーションでは、遠ざかるときに電車の表面に「UV」という文字が浮き上がるが、これはUV(紫外線)が出ているという意味ではなく、本来はUVだった光が赤方偏移により可視光として見えてくる、ということを表しているようだ。ちょっと紛らわしい表記方法なので、遊ぶ際には注意してほしい。
このすばらしいシミュレーションは、OpenRelativityというオープンソースのUnity用ツールキットを使って作られている。ほんとうはぼくもこれを使ってヘイル・メアリーのシミュレータを作ってみたかったが、Unityがうまく動かなくて断念した。だれか作ってくれることを期待している。
ペトロヴァ光が船の前方にどんどん集まってくるだって?
テレル回転はあくまで見かけの回転、ということはすでに説明した。実際には船は回転していない。船尾が見えたように見えるのは、単にあらゆる方向に拡散している反射光の一部がたまたまこっちの目に飛び込んできたからだ。だけどスピン・ドライヴから出る光はあくまで進行方向と反対の向きに噴射されている。だから、必ずしも噴射光そのものがこちらに向かってくるわけではないんじゃないか?
しかし調べていくうちに、さらに意味不明の現象を発見した。相対論的ビーミング効果、と呼ばれている。
いま、船が右方向にまっすぐ進んでいて、その後ろから光が噴射されているとする。このとき、船の速度を光速に近づけていくと、後方に向かって放射されていた光がだんだん前のほうに集まってくるらしいのだ! 具体的には、角度 $${\theta'}$$ のつもりが、以下の式で表される角度 $${\theta}$$ になる。
$$
\displaystyle \cos \theta = \frac{\cos \theta'+\beta}{1+\beta \cos \theta'}
$$
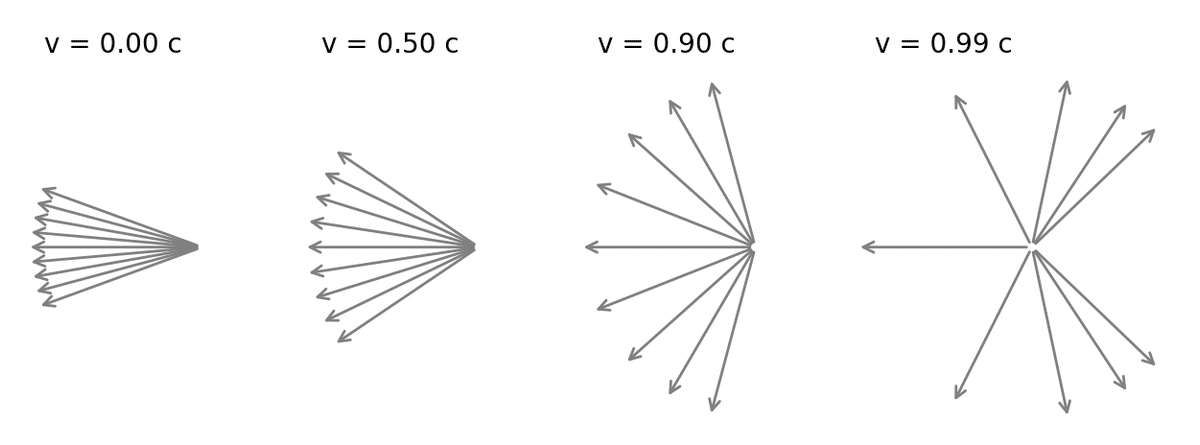
つまり、うんと光速に近づけば、船首側からでさえ、船尾の光が見えてしまうってことになる! だから、ヘイル・メアリーが地球に向かって加速しているとき、あるいはタウ・セチに向かって減速しているとき(どちらのケースも船尾はタウ・セチ側を向いている)でさえ、光がこちらから見える可能性はゼロではない。
信じられない話だが、実際に「ブレーザー」と呼ばれる天体ではこの現象が観測されているらしい。まったく……相対論ってやつはほんとうに奇妙だ。
スピン・ドライヴからはどんなふうに光が出ているのだろう?
ヘイル・メアリーの光が地球側にも飛んできているかもしれない、ということはわかった。問題は、どのくらいの明るさで見えるのか、ということだ。
スピン・ドライヴで1秒間に消費されるアストロファージは6グラムだ。$${E=mc^2}$$ より、スピン・ドライヴの光度は 5.393e+14 W になる。主人公も540兆ワットといっていたから、数字もちょうどぴったりだ(実際は消費されるのはニュートリノだけなんだけど、20ピコグラムのアストロファージがお腹いっぱいになると17ナノグラムになるらしいから、ほぼニュートリノの塊といっていい。おお……アストロファージの質量比は約850だ!)。これを1平方メートルあたりの値に換算しようとして、はたと手が止まった。
そもそも、スピン・ドライヴからはどんなふうに光が出ているんだろう?
スピン・ドライヴは直径4mのノズル3本から一方向に光を噴射している。だけどその噴射ビームも、さすがに完全にまっすぐそのままの強度で届くわけじゃないだろう。もしほんとうにそうだとしたら、もはや宇宙の秩序を乱す殺人ビーム兵器だ。たとえ何億光年離れようとも、「見えたと思った瞬間には死んでいる」ことになってしまう。実際には懐中電灯みたいに、裾野がちょっとは広がるんじゃないか? ——といっても、スピン・ドライヴの設計情報は本文にはほとんど載っていない。どれが実情に近いのか、さっぱりわからない。
というわけで、次の3種類のモデルを考えてみた。
ビーム:いちばん理想的な仮定。ノズルの幅のまま、光がビーム状にまっすぐ後方へ直進する。殺人兵器。実際にはこれよりは暗いはずだ。
コーン:中庸の仮定。懐中電灯のように、三角コーン(円錐)の形の限られた範囲に光が広がる。たとえば半頂角5度のコーンとしてみよう。
四方八方:いちばん保守的な仮定。星みたいに、四方八方に光が出る。ばかばかしいけど、相対論的ビーミング効果を考えればありえない話ではないし、ワーストケースを見積もるのには役に立つ。実際にはこれより暗くなることはないだろうってことだ。
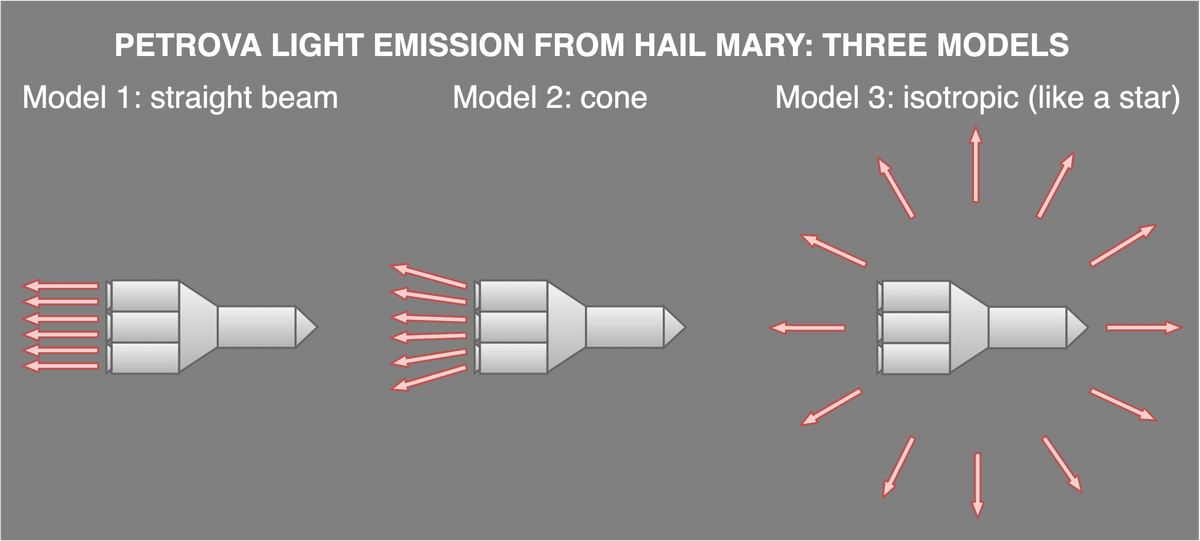
ビームモデルも四方八方モデルも、両極端の仮定だ。だから、きっとこの2つのあいだのどこかに答えがあるだろう、とあたりをつけることができる。
スピン・ドライヴが出しているエネルギー量はどれほどとんでもないのか?
さて、たとえばこれで、タウ・セチにいるヘイル・メアリーの噴射光を11.9光年離れた地球から見たらどうなるだろうか?
まず、ビームの場合だ。ビームの面積は直径4mの円筒形のスピン・ドライヴ3基分であると仮定する。この場合、スピン・ドライヴのノズルの前に立ったときとおなじ、1.430e+13 W/m2 の光が直撃する。ちなみに太陽表面でのエネルギーフラックスを計算したら 6.282e+07 W/m2 になった。
もうぼくの理解を超えている。太陽の表面も遠くおよばないほどだ。そう……太陽の表面にいるほうが、フル・スラスト時の〈ヘイル・メアリー〉のうしろに立っているより受けるエネルギーは小さいのだ。
ほんとうだ! 太陽の表面より10の6乗——100万倍もエネルギーが高いじゃないか! とんでもない殺人兵器だ。
今度はいちばん保守的な、四方八方に光を出しているケースはどうだろう。地球から見ると 3.379e-21 W/m2 だ。想像がつかないが、とんでもなく弱そうだということだけはわかる。そりゃそうだろう。ちなみに地球から太陽を見たときのフラックスは、1370 W/m2 らしい。
では、5度のコーンの場合は? 1.776e-18 W/m2。たしかに数字の上では、ビームと四方八方のあいだにはさまる、中庸な結果が出た。
ちなみに、この5度のコーンのケースで光が直撃しても死なないようにするには、ヘイル・メアリーからどのくらい離れればよいのだろうか?
地球における太陽のフラックス 1370 W/m2 と同じくらいのエネルギー強度になる距離をざっと求めてみると——4057 km。地球の半径が 6300 km なので、地球半径と同じくらい離れれば日なたぼっこくらいのエネルギーになるわけだ。
ここからわかることは、ヘイル・メアリーを出発させるときには、少なくとも数千kmくらいは地球から離してやらないと危ないってことだ! 逆にいえば、ヘイル・メアリーが太陽系のいろんな天体をビームでなぎ倒してしまうようなことはないとわかって一安心した。うっかりブリップAを蒸発させないでほんとうによかった……。ブリップAが、ちゃんとヘイル・メアリーのエンジンが停止してから近づいてきたのも、危険性をよくわかっているからだろう。
で、それは何等星くらいに見えるのか?
数字が W/m2 で出てきても、ほんとうに見えるのかどうか素人にはよくわからない。その筋の人ならわかるのかもしれないけど。
見えるとしたら夜空の星のように見えるはずだ。そこで、何等星くらいに見えるのかを計算してみることにする。なお、ここから先はこれまで以上に知識のない状態で、ググった式をなにも考えずに適用している。考え方が合っているのか、1ミリも自信がない。めちゃくちゃなことを書いていたら、どうか教えてほしい。お願いします。そっち方面の人。
1等星、2等星……ってそもそもどうやって計算するのだろう? ざっとググってみると、星の等級の決め方にもいろいろな種類があるらしい。輻射等級、ベガ等級、AB等級……頭が混乱する。どれを使えばよいんだ?
まず、一番かんたんそうな、輻射等級というやつだ。フラックス $${F}$$ の天体の見かけの輻射等級 $${m}$$ は、基準となる星のフラックス $${F_0}$$ = 2.5e-8 W/m2 を用いて
$$
\displaystyle m = -2.5 \log_{10} \frac{F}{F_0}
$$
で求められるらしい、とこのへんの資料に書いてあった。計算してみる。
ビーム:-51.89 等
コーン:25.38 等
四方八方:32.18 等
ビームは論外で当たったら即死なので無視するとして、コーンと四方八方はどんなものだろう。さすがに地上の望遠鏡では見えないだろうけど、ハッブル宇宙望遠鏡は31等まで見えるらしいし、もっとすごそうなジェイムズ・ウェッブ宇宙望遠鏡はさらに暗い天体でも見えるだろう。もしかして、今の技術でも見えるんじゃないか?(ちなみに、ペトロヴァ波長は大気をほとんど透過しない。だから宇宙から見たほうがいいのだ)
でも。さっきの資料をもう一度見返してみる。輻射等級は「すべての波長領域からの光の強さの寄与を足し合わせた」と書いてある。波長が決まっているペトロヴァ光の場合、ほかの波長成分はない。ペトロヴァ波長に全エネルギーが押し込められているのだ。だとすると、輻射等級はちょっとコンサバすぎるんじゃないか? 相変わらず自信はないけど。
というわけで、輻射等級よりもう少しめんどくさそうな、ベガ等級やAB等級とかいうものについても見てみる。ある波長帯に絞った明るさを表すことができるらしい。というか、ふつうは「等級」というと輻射等級ではなくて、これらのことを指すみたいだ。特定の波長帯に絞った明るさ——これなら、ペトロヴァ波長に向いている気がする。なんとなく。
えーと、まず分光放射密度という値に換算しないといけないらしい。単位はジャンスキー(Jy)というらしい。ジャンスキー。『コンタクト』って映画や『宇宙人かよ!』っていう漫画(どっちもぼくが大好きな作品だ。PHMが好きな人なら確実に楽しめると思う)に出てきたやつだ! と興奮する。でも意味も、Jy という単位も、今回はじめて知った。1 Jy = 1e-26 W/m2/Hz なんだそうだ。
……Hz で割る? どういうことだ? 単位にぼくは首をかしげる。Hzといえば周波数だ。ペトロヴァ周波数で割ってみればよいんだろうか? うーん。それになんの意味が?
さらにググる。ヒットしたこの資料を見ると「月に置いた携帯電話は50Jy」という計算をするのに、出力ワット数を携帯電話の帯域幅で割っている。
https://www.miz.nao.ac.jp/staffs/MarekiHonma/lecture/komaba2011-3.pdf
帯域幅? 携帯電話の帯域幅ならわかる。じゃあペトロヴァ光の帯域幅ってなんだ? ペトロヴァ光は波長が決まった単色光だ。理想的には、幅なんてほぼなさそうに思える。天体のスペクトルの輝線の幅を見積もる式みたいなのもググったら出てきたが、ペトロヴァ光には使えそうに思えない。
困った。
とりあえず、20μm付近の波長は天文学ではQバンドと呼ばれていて、一般にはその近辺の波長だけを通す光学フィルタを使って観測するらしいことだけは、わかった。ほら、主人公がアストロファージの走光性を調べるのに使っていたやつだ。Qバンドの帯域幅は、7.8μmらしい。だから、うんと大ざっぱに、フラックスが均等にこのQバンド内に分布していると仮定して、この7.8μmに相当する周波数帯域幅6THzで割ってみることにする。自信はない。まったくない。ああ、あと、ドップラー効果はひとまず無視する。
さて、分光放射密度的なものが出た。出たとしよう。これを $${F_{\nu}}$$ とする。これと、等級の基準$${F_{\nu0}}$$を使うと、等級 $${m}$$ が出るようだ。
$$
\displaystyle m = -2.5 \log_{10} \frac{F_{\nu}}{F_{\nu0}}
$$
やっかいなことに、この基準 $${F_{\nu0}}$$ にはいろいろな種類があって、「ベガ等級」(こと座の一等星ベガを基準とする測り方)だとベガの Q バンドの分光放射密度 $${F_{\nu0}}$$ = 9.70 Jy が使えそうだ(こちらのTable 7.5からもってきた。相変わらず自信はまったくない)。「AB等級」はベガを使わないで一律 $${F_{\nu0}}$$ = 3631 Jy を使うらしい。おいおい、なんで $${F_{\nu0}}$$ がこんなにちがうんだ?! 300倍もちがうぞ。いいのか。ほんとうにもう全然わからない。盛大に間違っていたら誰か教えてくれ……
これで、わからないなりに無理やり求めてみたのが次の数字だ。
ビーム:-63.48 等(ベガ等級)、-57.04 等(AB等級)
コーン:13.79 等(ベガ等級)、20.22 等(AB等級)
四方八方:20.59 等(ベガ等級)27.02 等(AB等級)
ビームは例によって無視して、とりあえずコーンと四方八方を眺めてみる。
うん、オーケイ……わからない。合ってるのかぜんぜんわからない。だけど、輻射等級よりは明るい見積もりになった。コーンの 13.79 等とかなら、宇宙望遠鏡のすごいやつとかを使えば、いけるんじゃないだろうか。
どのくらいの距離から、どのくらい見える?
さて、ここまでは、仮にヘイル・メアリーがタウ・セチにいた場合に、地球から見えるか? という話だった。
だけど、ヘイル・メアリーの出発直後、まだあまり地球から離れていない時期であれば、当然ながらもっと明るく見えたりするのではないだろうか?
ということで作ってみたのが下のグラフだ。「どのくらい離れたら、どのくらいの明るさで見えるか?」を示している。isotropicというのが四方八方、coneというのがコーンの設定。Bol、AB、Vega とついてるのはそれぞれ輻射等級、AB等級、ベガ等級だ。isotropic は少々やりすぎなので、たぶんconeを見るのがいい気がする。
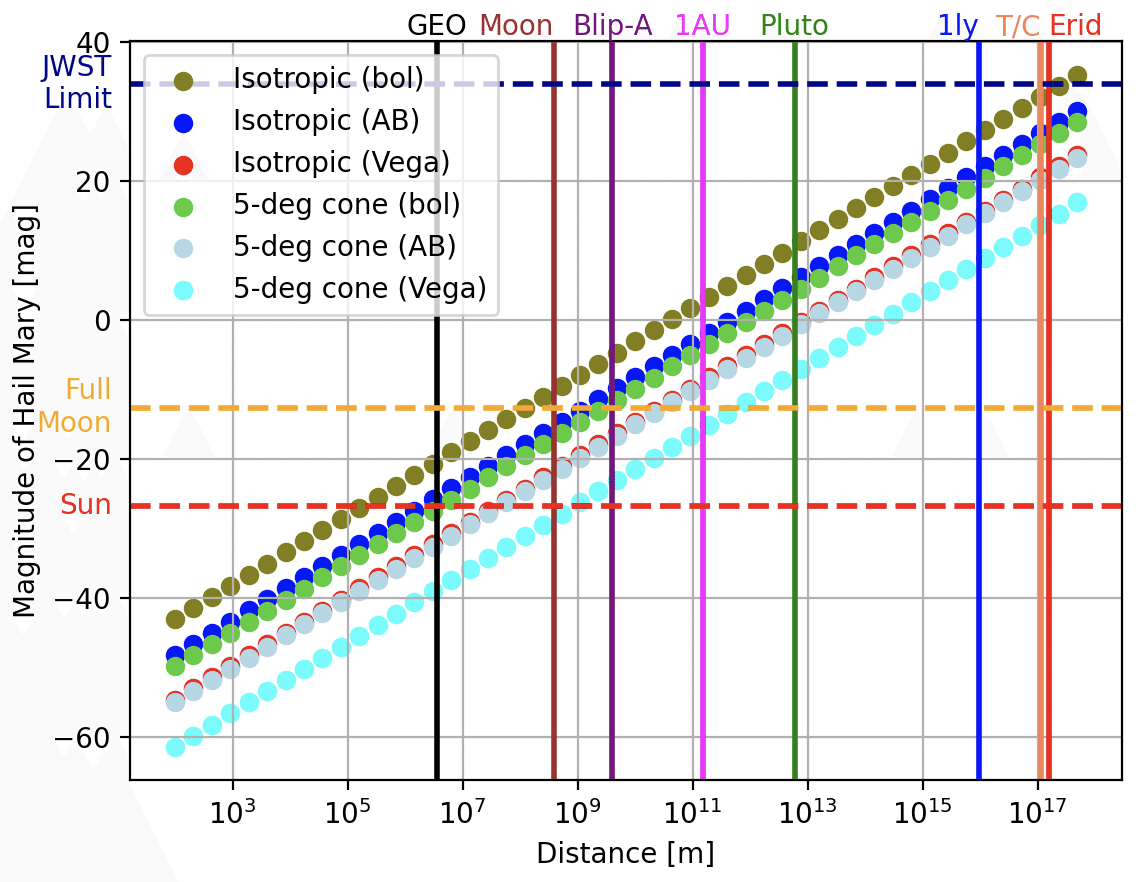
うーん、当たり前だけど、振れ幅が大きすぎる。エラーバー? 有意差? すまない、もはやそんなきちんとした解析ははぼくの手に負えない。これで許してくれ。
とりあえず、GEO(地球の静止軌道)では太陽より明るくなりそうなことがわかる。やっぱり地球のそばでスピン・ドライヴを動かしたら大迷惑だ。1AUでもまだ月ぐらいの明るさ、冥王星軌道あたりまで離れてもまだ肉眼で普通に見える。1光年くらいまでならそのへんの双眼鏡や望遠鏡で見えたりするかもしれない。
上のほうで計算したミンコフスキー図によると、1光年進むのに数カ月かかっている。つまり、ヘイル・メアリーが地球を出発してから、数カ月くらいはずっと見え続けてたんじゃないだろうか? ただし、ペトロヴァ光の波長はそもそも目に見えないし、地球大気をほとんど通らない。だから地上から人の目で見えたわけじゃないと思う。実際、ペトロヴァ博士もアタカマ天文台とかに確認をお願いしてようやくペトロヴァ・ラインを発見したわけだし。
ちなみに、Blip-Aと書いてあるのはちょうど400万kmの距離。これは、物語の終盤で主人公がタウメーバ漏れを発見して、ロッキーの船をいそいで探すときの両者の距離だ。スピン・ドライヴの殺人ビームをあたりかまわず振り回して大丈夫なんだろうか? と思ったけど、どうやらロッキーの位置から見れば太陽よりは確実に暗いらしくて、ちょっとほっとした。とはいえ、結構な閃光であることはまちがいない。ロッキーがブリップAのペトロヴァ光を定期的に光らせて、太陽系内での灯台代わりに使っていたのもうなずける。たしかにちょうどいい光源だ。
さらにちなみに、またもや Reddit でこんなポストを見つけた。先にタウ・セチに来ていたロッキーから、ヘイル・メアリーの光が見えたんじゃないか、という話題だ。
そりゃ、見えるだろう! といまなら自信をもっていえる。視覚を持たないエリディアンでさえも他の手段で気づくくらいには、ヘイル・メアリーの逆噴射はまばゆく輝いていたにちがいない。上のグラフをタウ・セチからの距離に適用すれば、少なくともあのファーストコンタクトの数カ月前くらいには、ロッキーは「ペトロヴァ光を放出する何かが近づいてくる」のに気づいてたんじゃないだろうか?
ちなみに、この質問者がこの考察をもとに書いた二次創作がAO3にある。ちゃんと計算に基づいて、ロッキー側の状況を丁寧に描写していて、すごくおすすめだ。
じゃあ、ビートルズは?
オーケイ。ヘイル・メアリーは意外と遠くからでも見えるらしいことがわかった。
では、ビートルズは?
ヘイル・メアリー本船と違い、ビートルズのスピン・ドライヴの具体的な出力は書かれていない(見落としていたら教えてほしい)。ただ、作中では3機のビートルズを使っていろいろアクロバティックなマヌーバをやっていたので、アンディ・ウィアーであれば確実にその出力を仮定したうえで、成立性を見積もっていたんじゃないだろうか。
読者が持っている情報は、アストロファージが125kg積まれていることのみだ。ビートルズはおそらく、加減速でこれをちょうど使い切るのだろう。ビートルズの加減速の仕方にはいくつか解釈がありうる、ということは上で見たとおりだけど、ここでは一番加速が穏やかな「4.8Gで20カ月」コースを採用して考えてみることにする(クレイジーな「500Gで12日間」コースだと、当然もっと明るくなる)。
ヘイル・メアリーは540兆ワットのエンジンで、200万kgのアストロファージを3.84年で使い切る。
ビートルズは「???」ワットのエンジンで、125kgのアストロファージを20カ月で使い切る。
ここから、単純にスピン・ドライヴの出力がアストロファージの消費率に比例するとするならば、
$$
\displaystyle 5.393 \times 10^{14} \text{[W]} \times \frac{125 \text{[kg]}}{20 \text{[mons]}} \div \frac{2 \times 10^6 \text{[kg]}}{3.84 \text{[yrs]}} = 7.793 \times 10^{10} \text{[W]}
$$
がビートルズのスピン・ドライヴの光度となる。ほんとうだろうか。あいかわらず自信がない。が、とりあえず先に進もう。同じようにグラフを描いてみる。
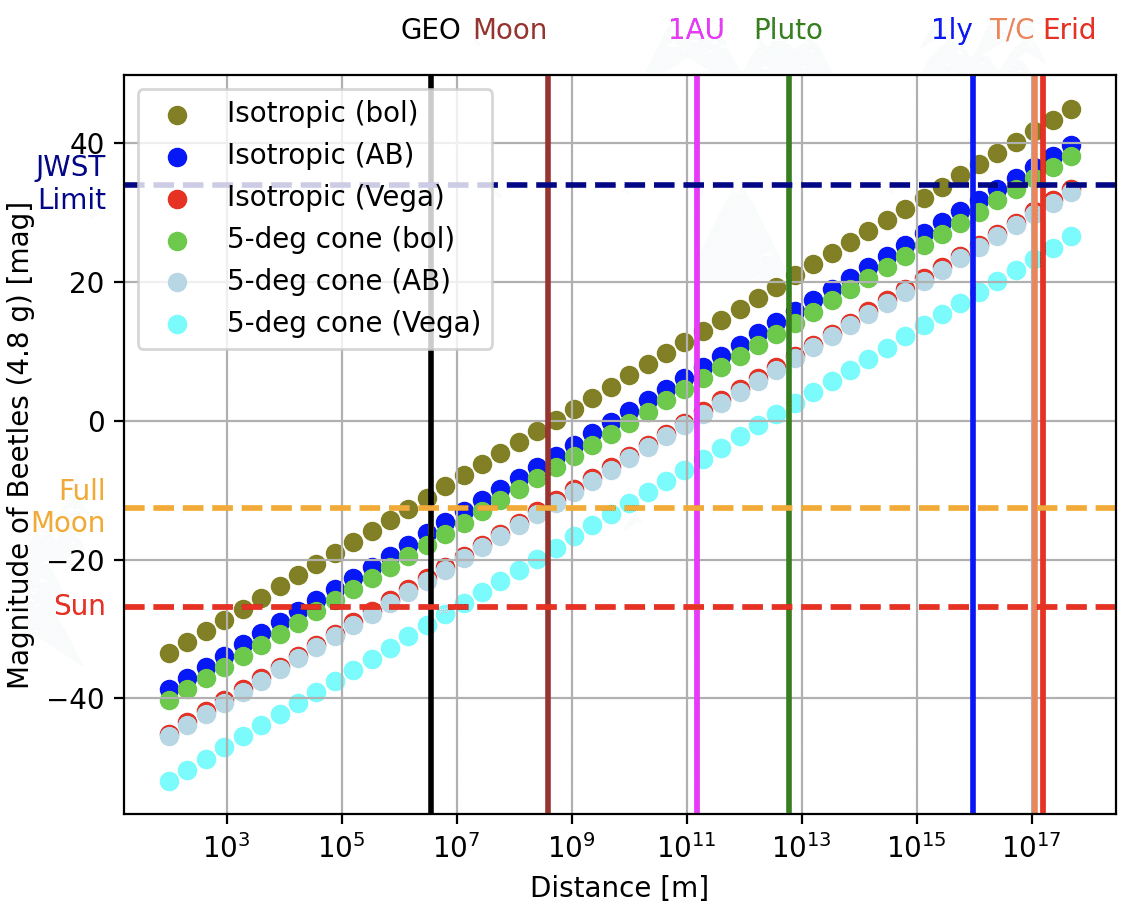
さすがに、ヘイル・メアリーよりはずっと暗い。どんなに楽観的に見積もっても、1光年以上離れたビートルズを見るのはかなり厳しそうだ。だけど、ビートルズが冥王星軌道あたりまで戻ってくれば、軌道上の望遠鏡であれば見えそうだ。
スティーヴ・ハッチは、ビートルズが「土星の軌道あたりまでもどってくれたら」地球からの電波を受信して、自分の位置や全データを地球に送り返すといっていた。だけどこの図をもとに考えると、きっと人類はもっと早い段階で——たとえば冥王星軌道のあたりで——ビートルズが帰ってきたことに気づけるんじゃないだろうか? 電波が届くよりも先に、スピン・ドライヴの光が見えるわけだから。
もっとも、そのためにはペトロヴァ光を軌道上から見張る必要がある。しかし、アストロファージという強力すぎる推進剤を得ている人類なら、今よりは宇宙開発のハードルがぐんと下がっていると思いたい。エネルギー的には、太陽系のどこに行くのも朝飯前になっているだろう。たとえ、ストラットのいう「地獄」のまっただ中に人類がいるとしても。ぼくは、そう信じたい。
(追記)噴射光の熱でエンジンが融けたりないのか?
この記事を読んで下さったなる10さん(ありがとうございます!)からこんな疑問が呈されていた。
そう言えば噴射光の熱でヘイル・メアリーのスラスターが融けてしまわないのは何でだろう… https://t.co/GTfwSKFqI1
— なる10🍥 (@naru_t_o) June 16, 2024
なぜスラスタが融けないのか。うん、さすが、至極もっともな疑問だ。
ジェットエンジンだろうがロケットエンジンだろうが、おおよそこの手の推進システムの開発はひたすら熱との戦いの歴史だったからだ。
ひたすら冷やす。熱くなる前に冷やす。ジェットエンジンはタービンブレードから空気を吹き出しまくるし、ロケットエンジンは極低温の燃料そのものをノズルスカートの周りに張り巡らせて冷やす「再生冷却」を用いている。らしい。完全にこちらからの受け売りだ。
ヘイル・メアリーも基本的にはロケットエンジンと同じことをやっている。いかにも既存技術をできるだけ生かすウィアーらしい発想だ。だけど既存のエンジンに比べてヘイル・メアリーが圧倒的に有利な点がひとつある。
アストロファージだ。やつらは96.415℃ 以上の熱はいくらでも吸い込む。すべてエネルギーとして蓄えてしまう。こんな理想的な冷却剤はない!
ヘイル・メアリーの船殻には、アストロファージの配管が張り巡らされている。放射線防壁にもなるし断熱材にもなる。もちろん燃料にもなる。なんて都合のいい存在なんだ! だからロッキーはアストロファージをエアコン代わりにもしていた。
「きみの船はアストロファージ冷却されている、質問?」 「イエス。アストロファージが船を冷やしている」 アストロファージ・コンジットはこういうときのために船体中にめぐらせてある。
オーケイ。たしかに船体はそれで断熱できるだろう。
しかし、スピン・ドライヴのスラスタそのものについてはどうだろう? 噴射光がまさに出ていく、いちばんホットな場所だ。船体とはわけがちがう。
そもそもエイドリアンでは、大気からの反射光ごときで、アストロファージ冷却されていた船体が融けたじゃないか?!
ぼくは船体が溶けることはないと思っていた。アストロファージが冷やしてくれているんだから、と! だがもちろん溶けるのだ。たとえアストロファージが完璧な熱吸収体だとしても(たぶんそうだとは思うが)、熱はアストロファージに吸収される前に金属に伝わってしまう。分厚い船体を通して熱がアストロファージに伝わるより早く船体の外層が融点に達してしまえば、アストロファージはなすすべがない。
うん。それについても、ウィアーは抜かりない。ディミトリは光のブラストが船に一切当たらないようにスピン・ドライヴを設計しているのだ。
普通のロケットエンジンの中では、燃焼ガスから生まれる推力は本来特定の向きを持たない。それを船尾の方向にすべて押し出すために、ノズルがある。ノズルは四方八方に向いた燃焼ガスの運動エネルギーを受け止めて、スロートから噴き出させる。だからノズルはめちゃくちゃ熱くなるのだ。
だけど、アストロファージは明確な走光性——赤外線(IR光)に向かっていく性質を持つ。だから、船体側から赤外線を当ててやれば、やつらはペトロヴァ光をかならず反対側に放射する。これが生物のすごいところだ。エネルギーは船体を一切直撃しない。だから、船体が熱くなることはない。ノズルも必要ない。
ぼくはかがみこんでじっくりと見た。「なるほど……これなら船のどの部分も光のブラストの範囲に入ることはないわけか」
文章よりもスピン・ドライヴの図や動画を見るのが早いだろう。素晴らしい図解や動画が公開されている。どちらも日本語なのでありがたい。動画はReddit のこちらの記事を参考にしているらしいが、記事のポスト主はアンディ・ウィアーに直接メールを送っていろいろ質問したうえで図を描いたようだ。
ああ、オーケイ。完璧だ。
噴射光は船にかすりもしない。ほんとうによくできている。
ただ、そうは言っても油断は禁物だ。満腹のアストロファージ1匹は1.5 MJのエネルギーを溜め込んでいるが、スピン・ドライヴではそれをたった4秒ですべて使い果たして死んでしまう(なかなか哀れではある)。1.5MJ ÷ 4秒 = 375 kW。ちなみに溶接用レーザは 1kW くらい、レーザ兵器は数十 kW くらいらしい。たとえ一匹でも、うっかり船体に向けて光を出さないよう、万全の注意を払う必要がありそうだ。
★『プロジェクト・ヘイル・メアリー』をもっと楽しむためのおもしろ情報源
さあ、まだまだ遊びたいネタはあるが、さすがに記事が長くなりすぎた。
ここから先は、ぼくが見つけた公式・非公式のPHMおもしろ情報を紹介していく。基本的にこの部分だけ楽しんでもらえれば個人的にはじゅうぶんだ。どれも、あまり日本のファンに知られていないんじゃないかと思っての紹介だけど、もしみんなとっくに知ってたら適当にスルーしてくれ。
「公式の」エリディアン設定集:エリディアン生物学
Reddit にはときどきアンディ・ウィアーが降臨しているのだが、とんでもないブツを見つけてしまった。
なんと、執筆時に使っていたエリディアンの設定集を惜しげもなく公開してくれているのだ!
(たまになぜか上記のスレッドに鍵がかかってしまっているときがある。その場合は下記のInternet Archiveを見てほしい。なお、設定集自体は以前と変わらず世界に公開されている)
とにかく、ダウンロードしてのけぞってほしい。情報量がとんでもない。英語が苦手な人も、DeepLやChatGPTを使って読んでみてほしい。ぼくもAI翻訳にひたすらお世話になりながら少しずつ眺めているけど、まだ全部読み切れてない。ぼくはいわゆる設定厨なので、こういうのにはほんとうに弱いんだ。
惑星エリドの性質や生態系にはじまり、エリディアンの見た目、生理学、生態学、文明……。作り込みのすごさに畏怖の念すら覚えるレベルだ。ぼくはこれを勝手にエリドペディアと呼ぶことにした。逆にロッキーたちエリディアンも、ラップトップの地球のWikipediaを読んでおもしろがってるんだろうなあ。この記事で生物学のことをほとんど扱っていないのは、ここに全部書いてあるからだ!
ちなみにエリディアン以外の項目についてはほとんど書かれていない。でもアンディ・ウィアーはきっと、あらゆる設定についておなじくらいすごい設定集を作っているにちがいない。アンディ・ウィアーも設定厨だ。ぼくはそう確信している。
日本語に翻訳しておられる方もいるみたいだ。
著者によるプロジェクト・ヘイル・メアリーの設定資料集eridian.docx↓↓
— 猫鮫 (@ScrrdSlsShnStr) December 7, 2023
全文Englishですhttps://t.co/eegljeMpKy
例のラジオで翻訳したものを共有してます↓↓ https://t.co/5CpBhyHpW1
ちなみに惑星エリド——40 Eridani Abという惑星は、実在する可能性が2018年に報じられて一躍注目を集めた(ちなみに一般には、『スター・トレック』シリーズの「バルカン星」候補としても知られている)。アンディ・ウィアーはおそらくこの報告の諸元(公転周期など)を作品に取り込んだのだろう。しかしこのたび、惑星かと思われていた信号が実は恒星由来であったという調査結果が報じられた。つい先週のことだ。
2018年の報告が否定されてしまったのは、PHMファンとしても残念だ。だがこれは決して「エリドが存在しない」ことを主張するものではない。なにかが「ない」ことを証明するのは非常に難しい。振り出しに戻っただけだ。エリダニ40の系外惑星については、さらなる研究の進展を待ちたいと思う。
ウィアー自身による『プロジェクト・ヘイル・メアリー』続編小説構想
アンディ・ウィアーのRedditでの発言のなかでも、とくにセンセーショナルなのは続編の構想だろう!
本気で続編執筆に取り組んでいるのか、まだ単なる構想段階なのかはわからない。だけど、少なくとも以下の2つのアイディアをアンディ・ウィアーは紹介してくれている。どちらも『プロジェクト・ヘイル・メアリー』本編の後日談、ヘイル・メアリーが地球を去ったあとの地球に関するものだ。あのあとの地球がどうなったか——読者なら気にならずにいられない部分だ!
まず、Saharan Caliphate という新国家の存在だ。うーん、日本語でどう訳せばよいのだろう。Caliphate はカリフ制国家のことだ。たとえばかつてのイスラム帝国がそうだった。1924年オスマン帝国を最後に正式に廃止されたが、最近になってカリフ制国家建設を主張する一派が現れたりと、ある意味でホットな話題だ。
この国家は2030年頃に誕生した、とコメントへのリプにある。また、決してその成立は平和的なものではなかった、とも。
https://www.reddit.com/r/vexillology/comments/15m5vai/can_i_request_some_flags_from_you_folks/
サハラ砂漠は、レデル博士がアストロファージを大量生産するためのブラックパネルを敷き詰めた地域にほかならない。この事業により、北アフリカの環境がめちゃくちゃになるだろうことは当初の段階から予想されていた。そして、アストロファージはヘイル・メアリーに搭載されて終わりじゃない。むしろ、その後の地球の命運を握る新エネルギー源そのものだ。アストロファージ産業は現在の石油産業を完全に置き換えるだろうし、その莫大な利権をめぐってきっとおだやかではない状況がいくつも発生したことだろう。
もうひとつは、アメリカによるカナダ併合だ。
https://www.reddit.com/r/vexillology/comments/15m5dzw/i_was_told_to_post_this_here/
世界が寒冷化した結果、カナダはどうやら居住不能になるらしい。アメリカはカナダの人々に市民権と居住権を与え、代わりにカナダの天然資源を得る、ということのようだ。アルバータの油田なども理由みたいだが——でもきみたち、96.415℃の永久熱源を持っているわけだよね? 6g で 540 テラジュールを生み出せる手段があるのに、1リットルで数十メガジュールしか生み出さない資源にしがみつく理由がある、質問?
うん、まあ、そんな単純な話ではないんだろうな。世界がアストロファージを持つ者と持たざる者に分断されていてもおかしくない。このあたりの話はきっと、ライランド・グレースよりエヴァ・ストラットのほうが一家言あるにちがいない。
カナダに住めないなら、アメリカの北部もほぼダメだろう。とはいえ、南極の氷を溶かしまくったから、南部の標高の低い土地だって決して安泰じゃない。歴史専攻だったストラットは(彼女の母国オランダもほぼ水没しているだろう)、何を思い、どう行動するだろうか、とつい考えてしまう。日本がどうなっているのかは想像もつかない。松家博士(英語がしゃべれないのが日本人としてリアリティ高い。でも研究者としてそれで大丈夫なのか)はどうしているんだろう。
アンディ・ウィアーはどうやら旗オタクのようで、星条旗の星の部分にメープルの葉が追加されたなかなか衝撃的な旗のデザインがポストされてたりするし、Saharan Caliphateの旗のデザインを募集したりもしている。「カッコいい旗に合わせて話を書き換えるくらいのことはするよ!」みたいなことまでいっている。まあ、その気持ちはよくわかる。旗とかロゴマークとかミッションパッチとか、そういうものは大切だ。
オーディブルに収録されている「ロッキーの声」
ロッキーの声!
そう、オーディブルだと、ロッキーの声が聴けるのだ! 和音で構成されたエリディアン語だ。
じつはロッキーの声は英語版と日本語版でかなり異なっていて、それがまたとてもおもしろい。
英語版は、周波数方向にも時間方向にも明確に離散的だ——おそらく人類とほぼおなじ全音階と、音符表記に忠実なはっきりした拍をもつ。たとえば「イエス」を表す♫♩はちゃんと「タタタン」というリズムで発音されるし、コードとして採譜もできるから、ラップトップでの解析も容易だろう。
ここにある記述によると、オーディブル版の制作にあたり、音符を実際の音に合わせたとのこと(ただしこの説明の一次ソースは不明なので、ほんとうにアンディ・ウィアーの言葉なのかはわからない)。
日本語版は、周波数方向にも時間方向にも連続的だ——音のピッチは連続的に上下し、拍という概念もなさそうだ(だから書かれている音符とは必ずしも一致しない)。チャープ信号とかポルタメントに近い。音の上げ方や下げ方(周波数の時間微分)にもなにか豊かな情報が乗っていそうな気がする。これは解析がむずかしそうだし、こちらからの発話はさらに骨が折れそうだが、「クジラの声」に近いのはこちらかもしれない。
あと、英語版は上下分冊になってないのでお得感があるし、なにより英語の勉強にもってこいだと思う。
ヘイル・メアリーの未公開図面(とアンディ・ウィアーの自宅と愛犬)
お次はCBSによる取材記事だ。2:13あたりのところを見てほしい。書籍に載っていた図とはすこしちがうヘイル・メアリーの図面が大写しになる。それほど目新しい情報はないが。
ほかにもこのインタビューにはいろいろとおもしろい部分がある。
彼の愛犬の名前はココアだ。白い犬だ。茶色ではない。散歩のシーンがある。
ガレージにいろいろな工作機械があって、「アルテミス時計」とかを自作している。完全にオタクだ。ぼくもオタクなのでよくわかるが、彼のオタクっぷりはすばらしい。
「COVID-19は人類史において最後のパンデミックになるだろう」という発言。うん、この潔いまでのベクトル、正直いってぼくはかなり好きだ。これぞ、彼の作品にいつも流れる、人類と科学に対する圧倒的な信頼と楽観性そのものだ。このインタビューを見て以来、スティーヴ・ハッチの脳内イメージが完全にアンディ・ウィアーになった。
ヘイル・メアリーの搭乗券
劇中でまさか実際にこんな搭乗券があったわけではないだろうが、どうやら本の販促用のようだ。バーコードを読み取ったら本のISBNだった。
Check out cool stuff about my next book: https://t.co/EP4lPGP7FK pic.twitter.com/Kpc9xVHEPw
— Andy Weir (@andyweirauthor) March 23, 2021
この搭乗券でぼくが好きなポイントは、「ペトロヴァ・タスクフォース」のロゴが入っているところだ。ストラット率いるあの超法規的な国際機関のことだ。日本語翻訳版では「ペトロヴァ対策委員会」と翻訳されていたけど、個人的には「ペトロヴァ・タスクフォース」と呼びたい。かっこいいので。
ヘイル・メアリーのミッションパッチ
上のほうでも紹介したけど、読み飛ばした人も多いだろうから、何度でも貼っておく。これもサイン本についていた販促用非売品だ。
UK fans, join our virtual book tour on the 5th May for an exclusive UK and Ireland event. More info at https://t.co/bl2gAqQ6ja
— Andy Weir (@andyweirauthor) March 31, 2021
Special bonus: buy book with ticket and you can claim an exclusive Project Hail Mary mission patch. pic.twitter.com/2i6Cn4MdH3
さて、ここから先はファンメイドの作品を紹介したい。
エリディアン時計シリーズ
オーケイ、みんな、エリディアンの数字の読み方は覚えてるかな? 位取りありの六進法を使っている(人類は10本の指から十進法になったのに、なぜエリディアンは5本の脚から六進法になったのだろう。ふつうは5を単位としてひとまとめにしそうなものだが)。ちなみに小説の最終章はVℓ章=50章(六進法で)=30章(十進法で)だった。ややこしい!
0:ℓ
1 :𝙸(セリフ体の「I」)
2:V
3:λ
4:+
5 :
V(よく∀で代用されているが、アンディ・ウィアーは実際には「V」+取り消し線でこの数字を表現している。さっき紹介した Eridian Biology がWord で書かれているので、そんなことまでわかるのだ!)
0、1の形はアラビア数字に近いし、2〜5も突起の数から類推しやすいので、慣れてくるとけっこう読めたりする。そんなエリディアンの時刻表記で、地球の時刻を表示してくれるサイトがある。
こちらはエリディアン時計の3Dプリンター用モデルだ。ちゃんと突起があって、エリディアンでも安心だ。どうせなら動いてほしかった!
こちらは、ほんとうに動くおしゃれなアナログ壁掛け時計だ。ただし、残念ながら時計の針はたぶん地球時間に合わせて進むんだと思う。
https://www.redbubble.com/i/clock/Project-Hail-Mary-Eridian-Clock-by-karistina/82912258.1X49C
ヘイル・メアリーの2D・3Dモデルとレゴ
本の冒頭にある(ネタバレ全開の)ヘイル・メアリーの全体図、どうも縮尺がいろいろと合わない。全長47mという記述もあったけど、そうするとものすごく細長い宇宙船になってしまう。
例によってRedditではみんな似たようなことを悩んでいるようで、より正確な縮尺で描き直したというポストがあった。アンディ・ウィアー本人にもOKをもらったという。これによると全長33mになる(上記のサターンVとの比較にはこの縮尺を使っている)。相変わらずどこに質量の20倍の燃料が積めるのかよくわからないが、バランスは良いと思う。
で、それを元にBlenderで作られたCG動画がこちらだ。ヘイル・メアリーが推進モードから遠心機モードに移行するところを描いている。ちょっと再生してみてほしい。
ワオ。言葉が出ないくらい最高だ。
やっぱり、宇宙機のリアルな機動には定番の『美しく青きドナウ』がよく似合う。とても優雅だ。
遠心モードのシーンを見ると、1周するのに18秒程度かかっている。本文中では毎秒20.71度で回転して1.00Gを生み出しているとのことなので、これは早回しでもスローでもない、実時間映像なのだろう。タウ・セチの光を浴びて回転するヘイル・メアリーの絵面はクールというよりむしろクレイジーで、こんなものを一か八かで放り投げたPHM世界の人類はやっぱり最高だと思う。
CG以外にも、超本格的な宇宙開発シムとして有名なKerbal Space Programでヘイル・メアリーを飛ばす人たちも現れている。やりたくなる気持ちはすごくよくわかる。
最後に、レゴを紹介しよう。レゴ社にはLEGO IDEASという、一般からアイディアを募集して製品化するクラファン的な企画がある。全世界から寄せられたアイディアのなかに、PHMがある。
企画自体は残念ながら期限切れになってしまったけど、すごくよくできている。ヘイル・メアリー、ライランド・グレース、ロッキー、星図(角度もたぶん合ってる!)がついている。船はパカッと開けて中にライランドを入れることができるし、遠心モードにもできる。
PHM映画版の監督であるフィル・ロードとクリス・ミラーは、『レゴ・ムービー』シリーズで一躍有名になったキャリアをもつ(『レゴ・ムービー』は大傑作なので大人にこそ見てほしい)。だから、レゴとPHMの組み合わせにはなんだかニヤニヤしてしまう。
* * *
——オーケイ。さすがに書き疲れた。だけど、あれこれ手を動かして計算してみる作業は、個人的にはほんとうに楽しかった。ウィアーの計算をなぞるだけの作業でさえ、きれいに理論と整合すること、さらにそこから小説に書かれていないことまで推測できてしまうことが、楽しくてしょうがなかった。相対論や天文学のびっくりするような雑学も知ることができた。最後にもう一度いうが、まちがいやおかしな点があったら(たぶんかなりある)どうか遠慮せずに指摘してほしい。
重箱の隅をつつくような野暮な指摘もかなりしてしまった。でも、アンディ・ウィアーは以前、こんなことをいっていた:
I slowly accumulated this core group of about 3000 readers over ten years of posting stuff to my website. And they’re all dorks, hard-core science geeks – because that’s the sort of stuff that I wrote. I’m one of those guys that’ll nit-pick every little physics problem in a movie!
(著者翻訳:ぼくはウェブサイトに作品をアップして、10年かけてこの3000人のコアな読者グループをゆっくり積み上げてきました。みんなガチの科学オタクです——だってぼくが書いたのはそういうやつなんです。ぼくも、映画に出てくるあらゆる物理について重箱の隅をつつくタイプなんです!)
ああ、なんだかすごく勇気をもらえる発言だ……(重箱の隅つつきに対する本作の防御が異様に堅いのは、ウィアー自身がそのタイプだからなのかもしれない。おおよそこちらが考えるようなツッコミはことごとく対策されているように思える)。
それであれば、この無粋な記事のことも許してもらえる、と信じたい。もちろん、もしなにか失礼なことや気分を害する内容を書いてしまっていたら、申し訳ない。修正したい。
このPHM世界には、まだまだいくらでも計算に値するネタが転がっている。今後もなにかおもしろいネタがあれば追記するかもしれない。
こんな酔狂な、長すぎる自己満足記事を一部でも読んでいただけたことに、ぼくはほんとうに感謝している。
そしてなによりもPHMの作品世界を細部まで計算可能な宇宙として設計し、検算し、描写し、共有してくれたアンディ・ウィアーに、心から敬意と感謝を表したいと思う。
* * *
「スキ」(♡)頂けると励みになります!
(noteのアカウントなくても匿名で押せます)
* * *
いいなと思ったら応援しよう!


