いろいろな力
独自研究です。要所要所ですっとぼけたことを言っている可能性があります。参考図書を提示しておきながら、その解釈を間違えていることすらありえます。そういう間違いをした時に参考図書の所為になったら嫌だな、という思いからの独自研究発言です。
色々な用語と定義
コンピュータによる流体力学 単行本(ソフトカバー) – 2012/6/5
J.H.ファーツィガー (著), M.ペリッチ (著), 小林 敏雄 (翻訳)
の場合
外力:圧力差、重力、せん断力、回転力、表面張力
これらは面積力(圧力、せん断力、表面張力など)と体積力(重力、回転力、遠心力、コリオリ力及び電磁力など)にわけられる。
数値流体解析の基礎 - Visual C++とgnuplotによる圧縮性・非圧縮性流体解析 - 単行本 – 2020/1/9 肖 鋒 (著), 長崎 孝夫 (著)
の場合
外力は面積力と体積力に分けられる。
面積力は圧力、粘性応力など
体積力は重力、電磁力など
外力(がいりょく)
ある物体に物体外部から作用する力。物体自身からは生じていない力。ベクトル量。
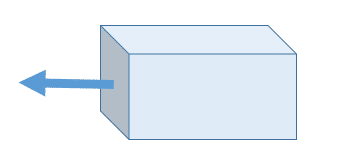
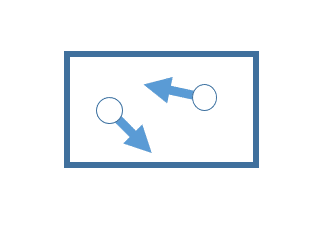
2次元にした分かり易いイメージの外力。
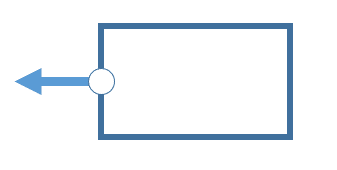
これも外力。
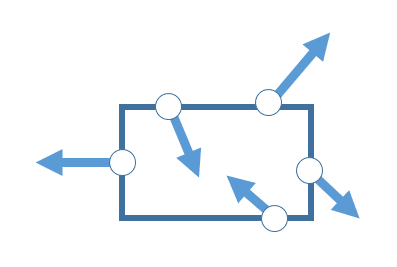
しかしながらこういうのも外力。
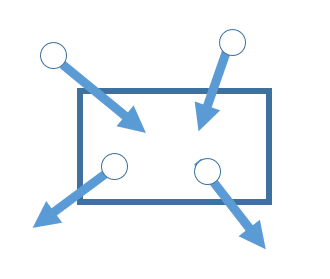
あまつさえこれも外力。
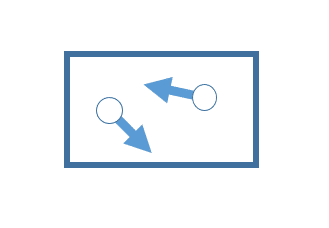
物体以外の出所から物体に対して与えられる力は全て外力である。打撃のように物体の位置的な外部から分かり易く与えられる外力もあれば、重力のように物体の位置的な内部であっても物体以外を出所として与えられる外力もある。
つまり空間上の位置や場所は必ずしも外力を定義しない。しかし位置や場所が物体を定義する上で欠かせない物であるなら、外力は位置や場所によっても定義することができる。
下図
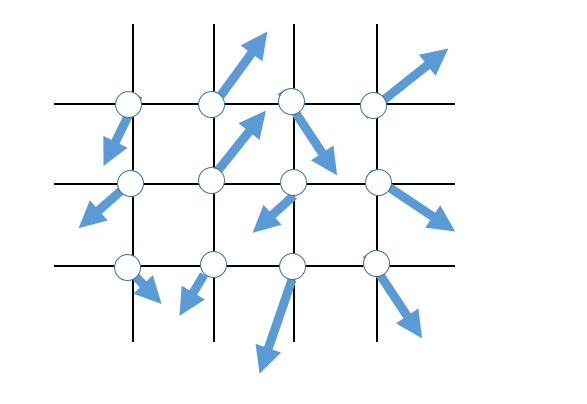
空間上の一点(二次元なら(x,y)、三次元なら(x,y,z))を指定した時に、その座標に生えているベクトルとしての外力。ベクトル場としての外力。例えば重力。
弾性力学 (日本語) 単行本 – 2011/11/10 荻 博次 (著)
表面外力、体積外力という呼称がある。
表面外力の場合、単位面積あたりに掛かる力をpとすると、ある点まわりの微小面積ΔΩを乗ずることでその点に掛かる外力ベクトルを得る。
体積外力の場合、単位体積当たりに掛かる力をGとすると、ある点まわりの微小体積ΔVを乗ずることでその点に掛かる外力ベクトルを得る。
表面力(面積力)
物体の表面積に比例する力を表面力(面積力)という。
例えば圧力、応力、摩擦力。他の物体との接触によって生ずるもの。
面積に比例するという以上の意味を持たないため、内力としても外力としても考えることはできる。応力はほとんど内力。というか応力は内力。とりわけ応力ベクトル(単位面積当たりの内力)は完全に内力。
物体力(体積力)
物体の体積に比例する力を物体力(体積力)という。
例えば重力、電磁気力、遠心力、コリオリ力。
体積に比例するという以上の意味は持たないが、文脈上ほぼほぼ外力とみなされる。というか物体力は外力。
多分、内力の定義が外力に抵抗するというだけというゆるやかなものならば、外力としての応力や内力としての重力も考えるだけなら出来ると思われる。
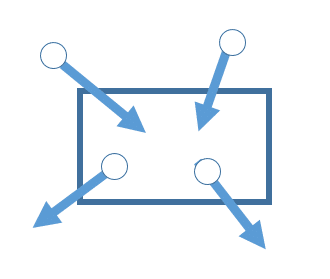
表面力と物体力を、外力の分類として見るやり方もある。
設計技術者が知っておくべき 有限要素法の基本スキル 青木隆平 (著), 長嶋利夫 (著) p19
有限要素法入門 (日本語) 単行本 – 1994/12/1
三好 俊郎 (著)p103
物体に作用する力は2種類(表面力と体積力)~物体にこれらの外力が作用するとその物体の内部にはその外力に抵抗する力が生じる。この力を内力という。
内力(ないりょく)
物体に外力が作用した時、外力に抵抗するために物体内部に発生する力を内力という。ベクトル量。
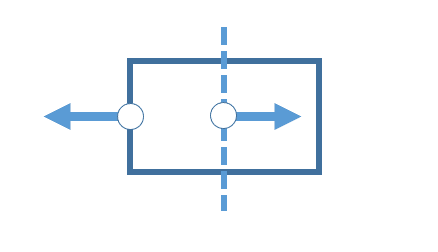
単純な位置関係で外力内力が決まるとは限らない的な話の通り、内力の内力たるゆえんは外力に抵抗するという部分であるであろう。外力に対する内力が無い場合、物体はふっとぶ、あるいは千切れる。(物体に作用する力が釣り合っている時、物体は静止するか等速運動する)
ただし力学などで用いる質点系や、プログラムなどで用いる離散系では外力内力を位置によって見ることができたりできなかったりする。なぜならば物体と物体以外を区別するのに空間中の位置を用いたり用いなかったりするからである。
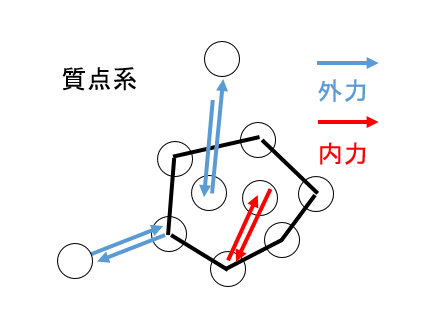
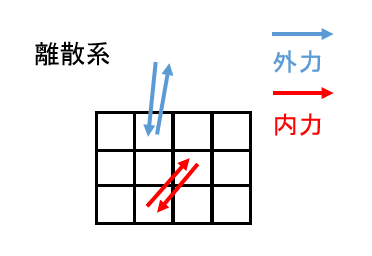
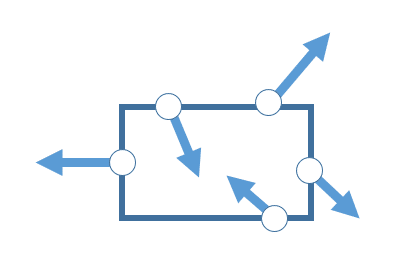
これは結局、ベクトルを始点終点の二点から求めているのであって、始点終点共に物体の内部であるならば内力。そうでないなら外力である。
また前提として、あるいは暗黙の内に、ある要素の近くの要素にしか力が及ばないというような約束事を導入してあることがある。特にプログラミング的なアルゴリズム、あるいは近似による数値計算を用いる場合にはそのようになるであろう。
このような図の見方をした場合、図におけるベクトルの長さは、力の大きさを意味しない。
二点によるベクトルを用いるならば、以下の図はやはり内力である。
応力:材料系
$$
応力[MPa]=\frac{力[N]}{単位面積[mm^2]}
$$
垂直応力は$${\sigma}$$、せん断応力は$${\tau}$$
古い圧力単位$${kgf/cm^2}$$とMpaは
$$
1[kgf/cm^2]=0.098[MPa]\\1[Mpa]=10.197[kgf/cm^2]
$$
ひずみ
$$
ひずみ=\frac{長さの変化}{元の長さ}\\ \varepsilon=\frac{\Delta l}{l}
$$
フックの法則
$$
\sigma=E \cdot \varepsilon
$$
せん断応力の場合
$$
\tau=G \cdot \gamma
$$
EとGは弾性係数
バネの伸びとして表される
$$
F=kx
$$
と同じもの。
ポアソン比
材が伸びるとそれに応じて断面積が小さくなる。その比。
$$
\mu=\frac{\varepsilon_l}{\varepsilon}
$$
$${\varepsilon_l}$$が横ひずみ
$${\varepsilon}$$が縦ひずみ
応力:連続体力学
ストレートな切り口はこちら
応力ベクトルと応力テンソルがある。
ただ単に応力と言った場合、とりわけ弾性力学や連続体力学では応力テンソルとみなすべきと思われるが、材料力学や構造力学の文脈では応力ベクトルである場合がある。あるいは応力テンソルの成分であることもある。あまつさえ内力一般である場合すらある。有限要素法の文脈では著者のキャリアによる。
物体に作用する力が釣り合っている時、物体内の任意の断面には内力T、及び単位面積当たりの内力である面積力tが発生している。この時のTを内力ベクトル。面積力tを応力ベクトルという。
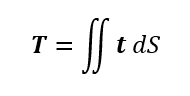
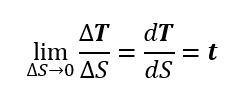
おそらくスカラーから作っていくパターンもある。この場合tは合応力と称する。
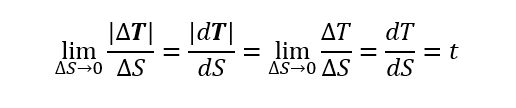
また
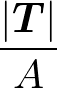
なるを単純に応力とすることもある。
断面に垂直なベクトルを法線ベクトルというが、面積力ベクトル(応力ベクトル)tは断面に垂直である必要はない。
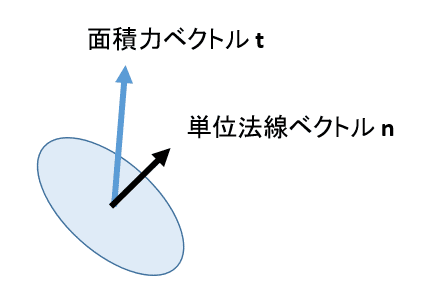
断面が微小領域ならば断面の形状は多分なんとでもなるのであって、それが三角形ならばxyz軸に張り付けることもできる。
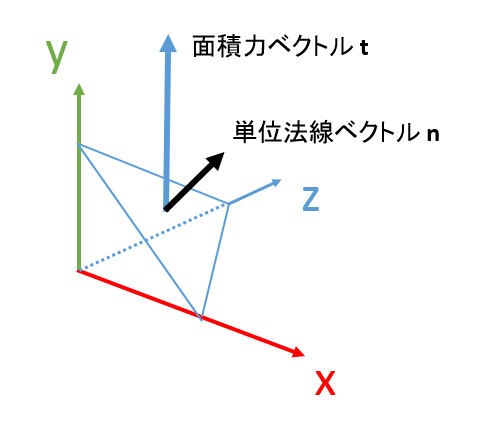
この時、微小単位のxy平面、yz平面、zx平面からも面積力ベクトルは生えてるのであって、やはり必ずしも各面に垂直とは限らない。

この時、過程は教科書
よくわかる連続体力学ノート 単行本(ソフトカバー) – 2008/12/19
京谷 孝史 (著), 非線形CAE協会 (編集)
を見てもらうとして、微小体積における力の釣り合いから
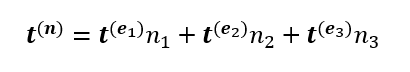
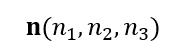
となる。各面積力ベクトルtは、右肩に乗ってる単位法線ベクトルによってどの面から生えているかを示す。すなわちtは肩に乗ってる単位法線ベクトルと同じ微小面から生える。(e1はyz平面、e2はzx平面、e3はxy平面から生える。教科書と軸の位置が異なるのは3Dグラフィックスの影響である)

ここでxyz軸からなる3つの平面の面積力ベクトルからなるマトリクスを応力テンソル

とすると

となる。これは
任意断面の面積力ベクトル(応力ベクトル)=(3平面の面積力ベクトルからなるマトリクス=応力テンソル)(任意断面の単位法線ベクトル)
となっている。

つまるところ、ある3次元空間中に存在する任意角度の微小平面に着目した場合、その微小平面から生える適当な面積力ベクトル(応力ベクトル)があって、その適当な面積力ベクトルを3次元空間の基本となる3つの直交かつ微小な平面(xy,yz,zx平面)から生える3つの面積力ベクトルに分解した時、それらの対応のための係数群となるのが応力テンソル。
逆に言えば座標軸に沿った素直な微小体積を考えた場合、3つの直交かつ微小な平面(xy,yz,zx平面)から3本の適当な面積力ベクトルが生えていると考えるなら、そいつらの成分全部集めたのが応力テンソルである。
任意面に掛かる内力に対する垂直・せん断応力は
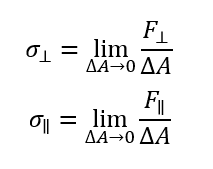
と定義されて、この時
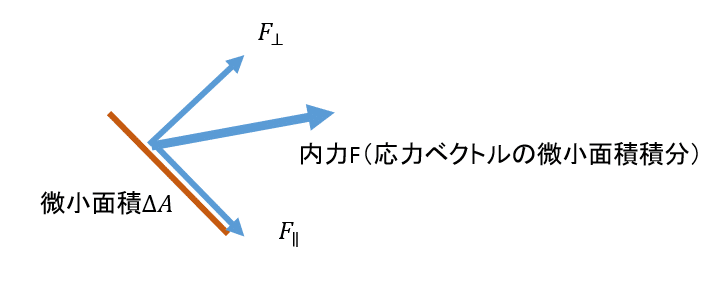
である。単位面積当たりでみると
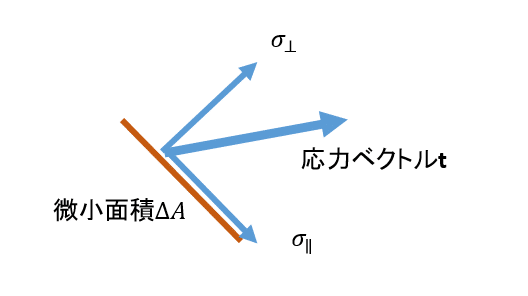
あるいは
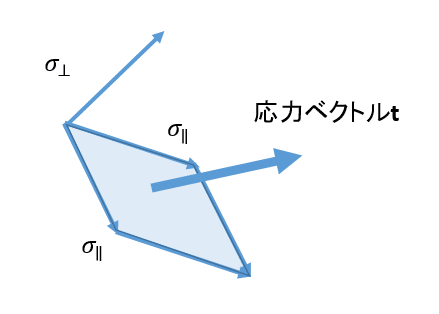
これを直交座標系の各面で見た場合
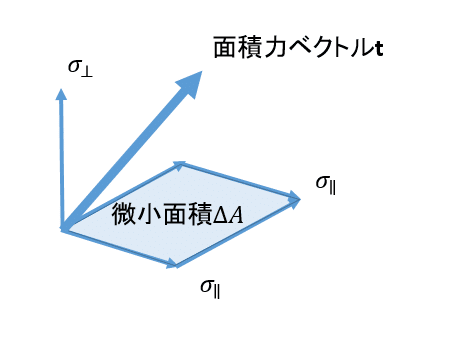
となって、上記の微小領域あたりの面積力ベクトル*3を求めるとその成分は応力テンソルの成分となる。その応力テンソル成分も垂直応力・せん断応力と呼称される。

材料力学系はある程度大雑把な概念から入る。
ごりごりの数学やら物理やらは連続体力学や弾性力学。
