[3D]座標の変換、及び座標系の変換①
※この記事の正当性は保障されません。
※2次元座標で記述しておりますが、必要に応じて3次元、4次元、あるいは同時座標に読み替えてください。
2次元の座標系は2つの基底ベクトルの組からなる。
系Aは最も基本的な基底ベクトル(1,0)(0,1)からなるとする。
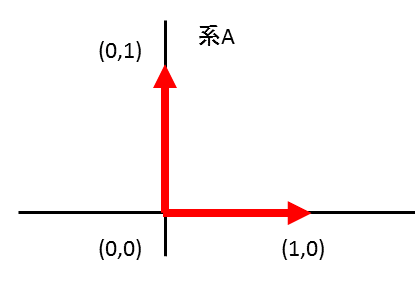
系はただのベクトルの組であるので行列で表すことができる。ここでは系を行列で表す時は縦ベクトルとして格納することを約束する。
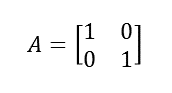

座標系がただのベクトルの組からなるのであれば、それらのベクトルを回転、拡大縮小、平行移動するなどすれば、別の新たな座標系になるであろう。
ここで系Bは系Aを反時計回りに45度回転させたものとする。
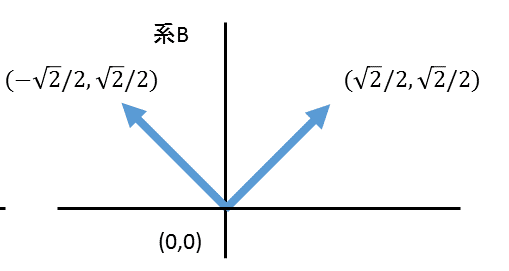
この時、系Bを行列で表すと
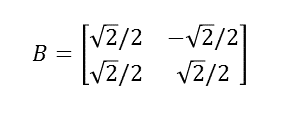

ある系における座標は、他の系から見てどのように見えるであろうか。
例えば系Aにおいて(1,1)にある座標は系Bからみてどんなもんであろうか。
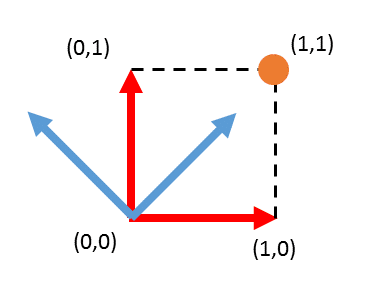
これはピタゴラス的に簡単に計算できて
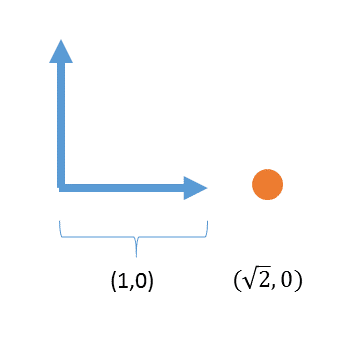
このことから、系Aを反時計回りに45度回転させた系Bから見た座標(√2,0)というのは、もともとの座標(1,1)を時計回りに45度回転させたものであると分かる。
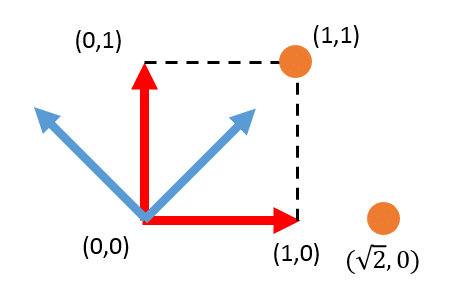
座標と系の関係を数式で見てみると、だいたい以下の関係になっていることが分かるであろう。系は基底ベクトルの組であり、系上の座標は基底ベクトルの線形和(基底ベクトルに係数掛けて足す)であるから
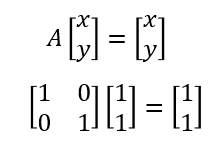
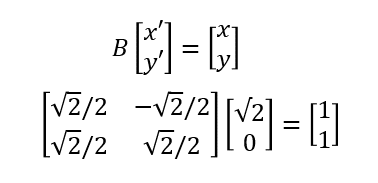
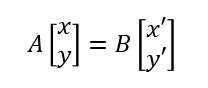
系Aの座標(1,1)を時計回りに回転させると(√2,0)になるのであったから
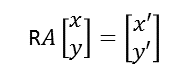
ここで回転行列は
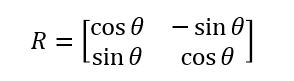
みたいな形をしていて、y軸+の方向に回転する(ディスプレイ座標ではy軸+の方向が下を向くため、回転が逆になることに注意を要する。最下部リンク参照)。とりま、時計回りに45度というのはここではマイナス45度の回転を意味していて
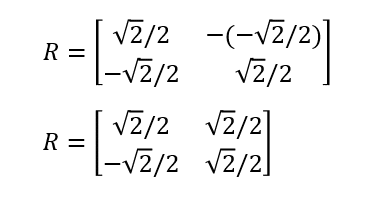
であるから
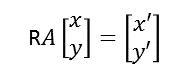
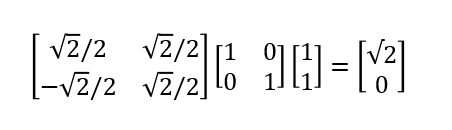
このことから結局
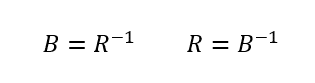
なのであって、簡単のために変換行列を回転だけにしてあるが、多分その他の変換、スケール、平行移動、スキュー、鏡映、投影についても似たようなことはできるであろうから、変換をまとめてMとすると
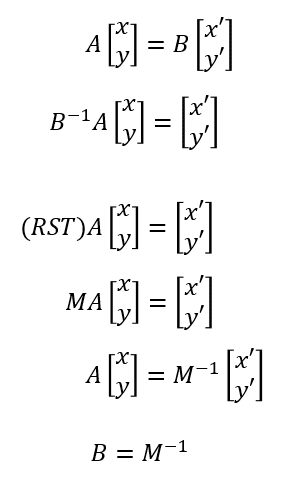
みたいになっているであろう。ただし平行移動は次元を一つ増やす必要がある。
これはつまり変換先の系、すなわち変換先の基底ベクトルの組が既知であるならば、その系の逆行列を取れば座標に対する変換行列は即座に求まるということである。
3*3や4*4の逆行列は力ずくで求めることができるし、それが直交行列であればただ単に転置すれば良い。
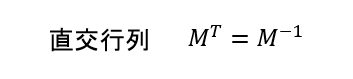
上の理屈でいうと、3Dグラフィックスで良く出てくるローカル座標→ワールド座標の変換(モデル変換)は
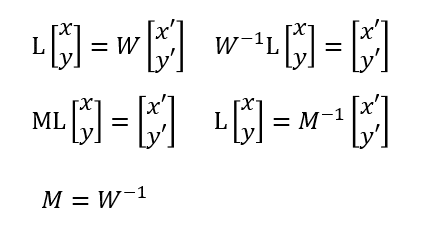
ワールド系を最も単純な正規直交基底、すなわち単位行列以外にする理由が特になければ、この変換はオブジェクトに応じてMから作った方が作り易いであろう。最も簡単なMは単位行列である。
ワールド座標→カメラ座標の変換(ビュー変換)も同じ要領のはずで
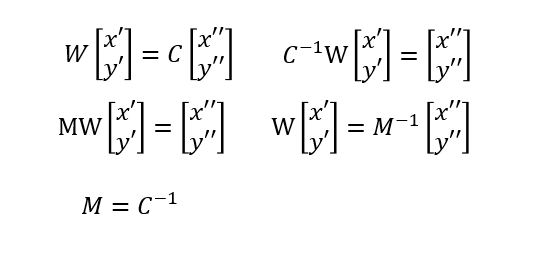
以下のプリントは以前に書いたやつ

カメラの位置座標と、見るべき対象物の座標、あるいはその2つのベクトルから導かれる視線の向きが決まっているなら、グラム・シュミット法的にカメラ系(基底ベクトルの組)を構築することができて、
Computer Graphics: Principles and Practice(Third Edition)のp304によれば

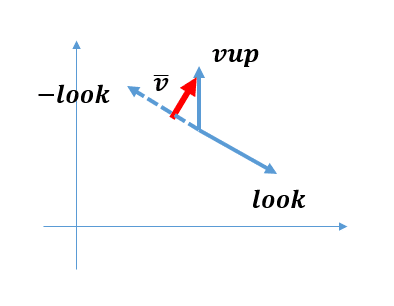
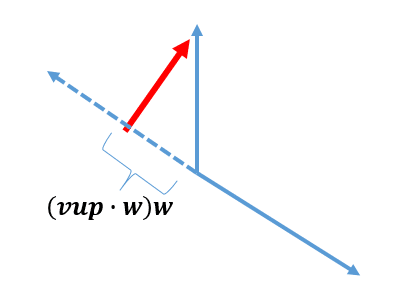
ここでvupは上方向、ワールド系の上方向ないし絶対系の上方向、よく読んでないが多分(0,1,0)あたりで良いであろう。(vup・w)wはvupが視線軸に落とす影ことprojectionであるからして、vup-(vup・w)wは視線軸からvup先端へ向かう垂直射影ベクトルとなる。以下参考。
二次元回転と加法定理
3Dグラフィックス入門:回転行列と右手系左手系の罠
C# : グラムシュミット法によるQR分解とQR法
