2023共通テスト生物問題解説シリーズ1 第6問A
2023年1月15日に行われた共通テストの生物の問題について考察をしていきます。問題の順番は順不同です。調べがついたものから解説していきたいと思います。
1 まず問題を見ておく。
まず『第6問A』のパートから。問題は以下のようなものです。


2 ヒカルさんとユウさんが見つけた論文とは?
二人が見つけた論文は、こちらだと思われます。

著者の井口恵一朗先生は現在長崎大学の教授で保全生態学がご専門であり、日野輝明先生は現在名城大学の教授で群集生態学がご専門である。井口先生が一貫してアユの研究を行っているので、井口先生が中心に行った研究なのだろう。井口先生は当時、中央水産研究所に所属していたようで、手短なまとめもWeb上に残っている。
この論文において、同じ大きさの水路に3匹、6匹、10匹、15匹、50匹のアユを放流した設定(図2(a))、そのあと個体数を変えて変化を追った設定(図3(b))が同じである。ほかにここまでよく似た設定の論文があるとは考えにくいし、現状ではほかに類似の論文は見つけられなかった。

Webのまとめによると本研究の成果は以下のようなものとなる。
以下引用
個体数密度が高くなるにつれて、なわばり個体の出現数は増加した(図1)。
個体数密度が高くなるにつれて、1個体当たりのなわばりサイズは減少した。(図2)
個体数密度が高くなるにつれて、各個体の成長速度は鈍くなるが、群れ個体がなわばり個体の成長を上回ることはなかった(なわばりは機能していた)(図3)。
アユのなわばりサイズは概ね1m^2であるという従来の所見は、否定された。
以上
3 論文から改変された部分
この論文に照らして問題を検証してみることにしよう。
まず表1の妥当性だが、「放したアユの個体数」「縄張り個体の数」「群れ個体の数」は該当論文と同じだが、「縄張りの大きさ(平均値,m^2)」は改変されているようです。

論文に掲載されている、魚の密度と縄張りの大きさの関係のグラフです。水路(池)E(50匹投入)での平均の縄張りの大きさは、目分量では0.5よりは大きいように見えます。

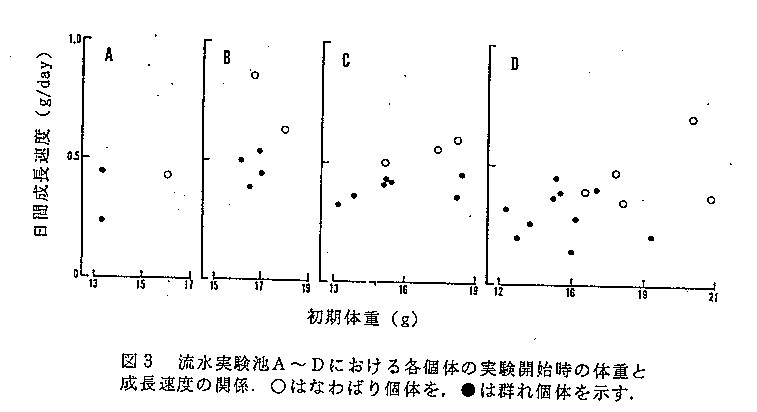
論文のFig.2を見ると分かるように、水路Eでは水路A~Dよりも縄張りの総面積が大きいのですが、共通テストの問題では、総面積が小さくなっています。これでは論文で示された「個体数密度が高くなるにつれて、各個体の成長速度は鈍くなるが、群れ個体がなわばり個体の成長を上回ることはなかった(なわばりは機能していた)」という知見が維持されるとは限らなくなります。Webのまとめページのグラフでは水路(池)Dでは、平均的には縄張りアユが成長速度が大きいが、縄張りアユと群れアユで成長速度が逆転する例が観察されています。論文のtable2に示されたデータによると、8月(3匹の縄張りアユと6匹の群れアユを取り除いた後※)では、成長速度の平均値が逆転しています。平均の縄張りのサイズが0.5m^2まで落ちたときに、縄張りアユがより成長できるといえるかどうかは、そのようになった場合を観察してみる必要があります。
※ In Pond C, two residents and four floaters were accidentally killed during removal and two new fish were introduced (group size = 6). From Pond D, three residents and six floaters were removed (group size = 6).

4 論文には存在しない実験2
さて前節で述べたように、実験2は論文には登場しない。一旦、縄張りを形成させてから、個体を加えたり、取り除いた実験はあるが(前節の※)、水路(池)Dからは3匹の縄張り個体と6匹の群れ個体を除去したものであり、水路(池)Eは8月しか実験をしていない。したがって、実験2の結果が実際にはどうなるかは、分からない。
5 選択肢を検討する
さて、選択肢を見ていくことにしよう。選択肢を掲載しておく。

① 最初から大きい傾向のあった縄張りアユの成長速度が大きく、小さい傾向のあった群れアユの成長速度は小さいことから、おそらく差が開いたであろうと想定できます。ただし、最大個体と最小個体の体重データは示されていないので、ひょっとすると差を縮める例もあるかもしれません。つまり全体の分散が問題になっているのか、最大個体と最小個体の差が問題となっているのか読み取りにくく、読み取り方によっては真偽の判定が困難です。
②縄張り個体数×縄張りの大きさを計算すると分かります。
水路A 7.2×1=7.2
水路B 3.6×2=7.2
水路C 3×2.4=7.2
水路D 5×1.3=6.5
水路E 10×0.5=5
さて、これが「違う」と言えるかどうかは微妙です。それぞれ一回の実験ですから、分散も分からず、有意差があるのかどうかも判然としません。高校生は統計的な検定の知識もないし、試験時間中にそんな計算をしている時間もないので、数値が少しでも違っていれば「変わらない」とは言えないと判断するならば誤りですが、科学的には判然としません。改変前のデータでも、縄張りの総面積は他より大きくなっているように見え、それをもって「変わった」と判断できるのであれば、データを変更する意味はなかったことになります。
③ 実験2については、論文に書いていない実験なので、ここからは架空の世界です。水路Dからは「縄張り個体」、水路Eからは「群れ個体」を除去しています。したがって水路Dでも当初より個体の大きさの分散は小さくなっており、そのときに「群れ個体になったアユより大きかった」という結果になるかどうかは分かりません。個体の大きさが近接している場合には、攻撃性、俊敏さなどの体の大きさ以外の要因が働く可能性が排除できません。
④ この選択肢も架空の実験に関するものです。群れ個体を取り除いているので、群れ個体が占めていた面積をめぐって、縄張り個体間の争いが起こり、その争いに敗れて縄張りを放棄した個体も現れたようなので、放棄しなかった個体がもっている縄張りの平均面積は大きくなったものと考えられます。40匹の群れ個体を除去し、10個体の縄張り個体だけを残したので、縄張り個体が3匹、群れ個体が7匹に落ち着く可能性もありますが、論文の池Cで6個体のアユがいる場合、当初導入した場合には縄張り個体が2、群れ個体が4になってもよさそうですが、増減実験のあとには5匹が縄張り個体になっていることから、増減実験後の縄張り個体と群れ個体の割合を、当初の導入個体数と同等になると考えて予測するのは困難です。
この中から、明らかに異なるものを選ぶとすると②になろうが、他の選択肢もほとんどが真偽不明である。本当に実験を行った場合には真になるかもしれないし、偽になるかもしれない。
6 なぜ実験やデータは改ざんされたのか?
データを改ざんし、実験を捏造してまで、真偽判定不能な選択肢を作った理由を考えてみたい。
たとえば、検定を行って有意差が検出され、検定がなければ有意差がはっきりしないような場合、検定の知識がなく、あるいは仮にデータセットを与えても試験時間中に解くことが困難である場合、たとえば平均値だけを比べて、差があるかどうかを判定できるようにするなど、論文の趣旨を曲げないように簡略化することは考えられるだろう。今回の場合には、論文の主張をおびやかしかねない改ざんが行われている。
選択肢の改善を考えてみよう。
① 実験1のどの池でも、縄張り個体と群れ個体それぞれの大きさの平均値は、飼育前より1か月後のほうが差が大きくなった。
とすれば、データから読み取れる内容になる。またはTable2の内容を掲載すれば、より分かりやすくなる。
② データを改ざんせず、論文のデータをそのまま用いても、縄張りの総面積は大きいほうにぶれているといえそうである。
③・④ まず実験2を入れなくても、実験1に関する論文に盛り込まれたデータを使えば色々作問はできそうである。たとえば、「個体群密度が大きくなるにしたがって、縄張りの最大の大きさは小さくなるが、最小の大きさは変化ない(池A(3匹導入)の結果から偽-1匹しか縄張りを作らずこれが最小であり最大である)」などのようなものです。さらに実験1では個体識別を行っていますが、これに関する選択肢はありません。論文のデータでは、縄張り個体が縄張りを維持している場合を調べるなど、個体識別のデータもありますので、それも選択肢に盛り込むこともできるでしょう。
7 まとめ
以上より、実験1における50匹導入した場合のデータ改ざんや、実験2のような実際には行われていない実験を導入することで、真偽不明の選択肢を作る意味がどこにあるのかは判然としませんでした。
真偽不明な選択肢を作ると、データの解釈に慎重な、真に科学的な思考ができる受験生にこそ不利益になります。真偽の判定が可能なものと想定し、何度も問題文と選択肢の文章を読み、時間を使うからです。この問題では、「考える力」というのが、問題文中の「実験前の体重が重かった個体が縄張り個体に、軽かった個体が群れ個体になっていた」「 実験期間中の体重増加量は、どの水路でも、縄張り個体になったアユが、群れ個体になったアユよりも大きかった」「アユの食物は水路の底面に生える藻類のみであり、 同じ水路内において、縄張り個体間で縄張りの大きさにほとんど違いはなかった」といった、実態とは異なる宣言を受容し、それがあたかも条件によらず常時成立する法則とみなすという、科学からは遠い態度を涵養することになってしまっているのです。
