【合成抵抗応用】複雑な電気回路を計算していこう!! 電気回路を解き明かすには。授業でつまづきやすいところや資格挑戦レベルまで。

はじめに

　今回はついに、本格的に電気回路へ取り組んでいきたいと思う。物理の授業や、電気工事士、欲を言えば電験三種でも、基礎として出題されるような問題となってくる。電気系の資格取得を考える人や、高校生で電磁気学を復習しようという人は、軽々と解いてしまってほしい。また、電気回路を解く手段は数多ある。たまたま私と波長の合う人はいいが、違う方法で解けてしまうのなら問題ないので、そこだけは注意してほしい。逆に私も思いつけないものかもしれないので、自信のある人には是非コメントして教えていただきたい。もしかすると記事で紹介するかもしれない。
　また、今までに書いてきたことは、今回とこれ以降の基盤となるものであるから、電気基礎に自信のある人（そんな人はそもそもこの記事を読んでいないだろうが）を除いて一度は確認しておいてほしい。

↓特にこの内容はわかっていなければ話にならない

確認

　私たちにできることは以下の通りだ。

①抵抗とそれに加わる電圧、および流れる電流の　　値を求めること。（オームの法則）
②複数の抵抗を、一つのものとみなすことで纏めること。（合成抵抗の計算）

この二つのから、複雑な回路でも抵抗を少しづつまとめていき、簡素な回路となればオームの法則により値が求まるということだ。これを頭に入れて、「回路を解くために何がしたいか」自分で考え付くことが重要だ。

問題

　以下の回路を使って練習してみよう。ab間の合成抵抗を求めるなんて問題が電気工事士の最初の問いではよくある。

出典：令和6年度下期第二種電気工事士試験

ここでは、ab間に24Vの電圧を加えたことににして解いていこう。24V電池の＋をa、－をbにつないだのと相違ない。また、「回路を解く」とは、「どこにどれだけ電流が流れて、電圧降下がどれだけ発生するのかを明らかにすること」としていて、今後もそうする。
　簡単に求まる値から順に出していこうとすると、まず一回の計算で分かることがある。それは、上の6Ω抵抗に流れる電流である。わからなかった人は、電圧について以前までの記事で復習してほしい。6Ω抵抗の左端とa、右端とbで、電気的エネルギ、すなわち電位が共通すると確認できるはずだ。なぜならそれらが、抵抗に阻まれていないから。そうと分かれば6Ω抵抗に加わっている電圧も、電源と同じ24Vとすっかりわかる。であれば、オームの法則により一発で4Aと求まるのだ。

　こうしてひとつずつ明らかとしていく。次は下部分がどうなっているか見ていこう。抵抗が多く複雑なので、左下で一つ、右下で一つと考える。そのまとめた抵抗値は、和分の積で1Ωと2Ωと分かるだろう。では、その二つの抵抗はどんな接続か。直列接続となっていると分かったならば合格、足すだけで更にまとめることができた。以上の文章で書いたものをまとめると、下図のように簡単な回路と見立てることができる。ちなみに、このように性質が同じとなる回路を等価回路という。

問題と等価な回路

これ以上文を書いて説明していくことは蛇足だろう。結局、この回路は2Ωの抵抗に24Vの電圧がかかり、12Aの電流が流れているというのが正体だ。こんな風に、電気回路を解いていきたいなら、自分が理解できるところまで簡単な等価回路をつくっていき、オームの法則によりとどめを刺すという風になってくる。　
　ちなみに、賢い読者のなかには、なぜ私が4Aをださせたのか、最初から全体の合成抵抗を出せばよかったと思う人もいるだろう。それは、次に解説することの導入としたかったからだ。余裕のある選ばれし人たちは、この後も見ていってほしい。どんな問題（電験三種や入試問題等）にも対処できる、応用力が身につくだろう。

上級の問題の一一例

　一気に難易度は上がるが、今までに解説したものを応用していけば解くことができる。その応用について次項から解説するが、詳しく問題の解説が必要ならば、コメントを待っています。

出典：令和6年度第三種電気主任技術者上期試験　理論科目

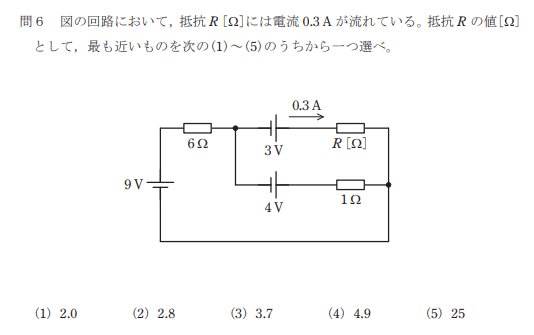
オームの法則の真価

　これまでの記事で、私はオームの法則を最強だとかいって持て囃してきた。読者のなかには、いいすぎだと思ったものも少なくないと思う。しかし、これからの説明でその考えを改めることになるだろう。これを理解できてこそ応用の道が開ける。