微積で考える物理~力学編①~

2025年2月24日 12:34

それでは今回は、高校物理の力学についてのお話をしたいと思います。前回は微分積分の話を長々としたのもあるので、今回はその微分積分を当たり前のように使っていきますから皆さんどうかついてきてください(汗)

さて、前回の「微分積分と『みはじ』の式」では時刻tにおける
･物体の移動距離x(t)
･速さv(t)
･加速度a(t)
はそれぞれ次のように表されることを学習しました。

v(t) = dx(t)/dt …(a)
a(t) = dv(t)/dt = d^2x(t)/dt^2 …(b)

[図1] 移動距離の求め方のイメージ
時刻-速さのグラフにおいては、曲線下の面積が移動距離に相当する

これより、a(t) = a(定数)、つまり等加速度運動を考えると、(b)より

a = dv(t)/dt
∴ v(t) = a∫dt = v0 + at (ただしv0は初速度)

であり、さらに(a)より

v0 + at = dx(t)/dt
∴ x(t) = ∫(v0 + at)dt = v0･t + (1/2)at^2 + C
(Cは積分定数)
x(0) = C = 0より
x(t) = v0･t + (1/2)at^2

という式が導かれます。
ここからさらに、

{v(t)}^2 - v0^2 = (v0 + at)^2 - v0^2
= 2v0･at + (at)^2 = 2a{v0･t + (1/2)at^2}

∴ {v(t)}^2 - v0^2 = 2ax(t)

という式が導き出されます。
今回はまずこれらの式を基にして、物体の鉛直投げ上げ運動を考えたいと思います。

❶ 運動方程式

まず鉛直投げ上げ運動を考える前に押さえておきたいのが、運動方程式の考え方です。
一般的に物体の加速度a[m･s^-2]は、その物体に働く力F[N]に比例し質量m[kg]に反比例することが知られています。

a(t) = F/m ∴ ma(t) = F : 運動方程式

この関係式を運動方程式と呼びます。この運動方程式、ma=Fのたった4文字で表される式なのですが、実はこの式から様々な力学に関する式を導出できるのでたかが4文字、されど4文字なのです。
まず、この運動方程式の両辺ををtで積分してみましょう。

m∫a(t)dt = ∫Fdt
⇔ mv(t) = ∫Fdt (またはFΔt = mv(t)などと表現される場合もあります。)

このmv(t)は力積と呼ばれ、物体に加わる衝撃の強さを表します(力積は撃力とも呼ばれることがあります)。また力積は運動量とも呼ばれ、衝突する物体どうしの運動量の和は常に一定であることが知られています。これは運動量保存則として一般的に知られています。
なお、衝突する物体どうしには次のような反発係数eが定義されます。

反発係数e = -(u1 - u2)/(v1 - v2)
= (2物体が遠ざかる速さ)/(2物体が近付く速さ)

また物体に働く力Fをx(t)で積分することにより物体にした仕事、つまり物体に与えた(力学的)エネルギーが得られます。
ma(t) = Fより、Fをdx(t)で積分すると

K = ∫Fdx(t) = ∫{ma(t)}dx(t) = m∫{dv(t)/dt}･dx(t)
= m∫{dx(t)/dt}･dv(t)
= m∫v(t)dv(t) = (1/2)m{v(t)}^2 + C
(Cは積分定数)

となります。ここでは物体の速さによる力学的エネルギー、つまり運動エネルギー以外のエネルギーを考えないためC=0と見なして差し支えありません。つまり、

K = ∫{ma(t)}dx(t) = (1/2)m{v(t)}^2

ということになります。これが物体の運動エネルギー(kinetic energy)Kの式になります。

○「仕事」

ところで皆さん、中学の理科の授業で「仕事」という言葉を聞いたことはないでしょうか。一応断っておきますと、社会人の方々が普段からされている「お仕事」のことではありません。(笑)
物理で定義される「仕事」とは、物体に力を加えてその物体が移動したときに、加えた力の大きさ[N]と物体の移動距離[m]の積で表現される物理量を指し、エネルギーと等価な物理量になります。そのため、エネルギーと同じく単位に[J]を使用します。

(仕事[J]) ＝ (加えた力[N])×(物体が動いた距離[m])

この「仕事」に関連して、物体に働く重力がする仕事を位置エネルギーと呼びます。ある基準点から高さh[m]の位置にある物体の位置エネルギーUはU=mgh[J]と表されます。

U = ∫[0,h](mg)dx = mg∫[0,h]dx = mg[x][0,h] = mg(h - 0)
∴ U = mgh

運動エネルギーの式K = (1/2)mv^2と位置エネルギーの式U = mghの2つを用いると、基準面からh[m]の高さで物体を落下させたときの、着地直前の物体の速さvを求めることができます。

mgh = (1/2)mv^2 より
v^2 = 2gh ∴ v = √(2gh) (∵v>0)…(※)

vが常に０より大きくなるのは、難しい話になりますがvがベクトルの大きさ(=スカラー量)を表すからですね。スカラー量とは簡単に言えば、体重(質量)や身長のようにマイナスが絶対に付かない量だというイメージを持ってもらえれば十分です。
(※)式を見てもらえればお判りいただけるでしょうが、着地直前の速さvは物体の質量mの大きさにより変化しない値になります。

なお少しマニアックな話にはなるのですが、特殊相対性理論を用いた運動エネルギーの式の証明方法もあります。

〇特殊相対性理論

特殊相対性理論においては、運動している物体の質量(=相対論的質量)は静止している物体の質量(静止質量)より大きく、その差は物体の運動エネルギーに相当する質量差であるとしています。
現実には有り得ない設定ではあるのですが、例えば上の[図4]のように観測者が下から質量M[kg]の物体Aと質量m[kg]の物体Bを観測しているものとして、BがAに向かって水平方向に光速c=3.0×10^8[m･s^-1]で近付き、なおかつ観測者はAとBに対して鉛直下向きにv[m･s^-1]の速さで遠ざかる場合を考えます。なお、AとBは衝突後に一体となって運動するものと仮定し、Bは光子(X線やγ線)と同じ波動性を持つものとします。つまり、Bの運動量pはその(運動)エネルギーEに対してp = E/cと表されるのですね。
このとき、観測者から見てAとBは鉛直上向きにv[m･s^-1]の速さで運動しています(この場合、観測者は静止していると見なしてAとBの見かけ上の速さをv[m･s^-1]としているのですね)。BはAに向かって水平方向に運動していることから、Bにおけるv[m･s^-1]の大きさの速度ベクトルと水平方向の速度ベクトルの和は斜め上方向の速度ベクトルとなります。ここで特殊相対性理論の基本的原理である光速度不変の原理を適用すると、この斜め上方向の速度ベクトルの大きさはc[m･s^-1]と見なすことができますから、Bの初期運動エネルギーをE_0として鉛直方向の運動量保存則を立式すると

Mv + (E_0/c)･(v/c) = (M+m)v
⇔ (E_0/c)･(v/c) = mv
⇔ E_0/c^2 = m
すなわち E_0 = mc^2 …(＊)
これがBの静止エネルギー(静止質量)と定義されます。

次に、天井に設置した鏡と向かい合わせに光源を置いた車を、v[m･s^-1]の速さで走らせる場合を考えます。このとき光を前述の静止質量m[kg]の粒子と見なして、車が運動しているときの粒子の質量、つまり相対質量をm'[kg]とすると、運動量保存則より
mc = m'･√(c^2 - v^2)　⇔ m' = (mc)/√(c^2 - v^2)
すなわち
m' = m/√{1 - (v/c)^2} : 相対論的質量

となります。よって相対論的エネルギーEは

E = m'･c^2 = (mc^2)/√{1 - (v/c)^2} …(＊＊)

と表されます。
さて、前述で述べました通り物体の相対論的エネルギーは静止エネルギーに運動エネルギーを加えた分のエネルギーとなりますから、物体の運動エネルギーはその物体の相対論的エネルギーから静止エネルギーを差し引いた差になります。

運動エネルギーT = E - E_0

よって(＊)と(＊＊)より

T = (mc^2)/√{1 - (v/c)^2} - mc^2
= [1/√{1 - (v/c)^2} - 1]･mc^2

ここでc=3.0×10^8[m･s^-1] >> vとすれば
v/c <<1ですから、マクローリン展開を用いると

1/√{1 - (v/c)^2} = {1 - (v/c)^2}^(-1/2)
≌ 1 - (-1/2)･(v/c)^2

よって

T = [1/√{1 - (v/c)^2} - 1]･mc^2
≌ {1 - (-1/2)･(v/c)^2 - 1}･mc^2
= {(1/2)･(v/c)^2}･mc^2
= (1/2)mv^2

となり、前述の運動エネルギーを求めることができるのですね。

❷ 重力加速度g

さて、本題に戻りますが、地球上に存在する全ての物体には重力と呼ばれる力が働きます。重力とは地球の中心に向かって働く、地球と物体の間の万有引力と広義的に解釈することができます。
この重力は物体の質量m[kg]と重力加速度g=9.8[m･s^-2]の積で表現されます。つまり、重力はmg[N]と表されるのですね。
先程の運動方程式ma(t) = Fにおいて、F=mgを代入すれば
ma(t) = mg ∴ a(t) = g
重力加速度gは地球上に存在する限り鉛直下向きに一定の大きさで働く加速度ですから、初速度0[m･s^-1]で物体が鉛直下向きに落ちる運動は等加速度運動になります。

v(t) = v0 + at (ただしv0は初速度)…(a)
x(t) = v0･t + (1/2)at^2…(b)
{v(t)}^2 - v0^2 = 2ax(t)…(c)

よって上記の(a)~(c)の3式に対してa = gおよびv0=0を代入すると、鉛直下向きに物体を初速度v=0[m･s^-1]で自然に落下させる運動を表現した式が得られます。

v(t) = gt (ただしv0は初速度)…(a)'
x(t) = (1/2)gt^2…(b)'
{v(t)}^2 = 2gx(t)…(c)'

特に(c)'式は前述でお話しました力学的エネルギー保存則から求めることができます。

○鉛直投げ上げ運動

また(a)~(c)の3式に対してa=-gを代入してx(t)→y(t)(=物体の上昇高度)と置換すると、物体の鉛直投げ上げ運動を表現した式が得られます(ただしこのとき、空気抵抗の影響は無視できるものとします)。

v(t) = v0 - gt …(a)"
y(t) = v0･t - (1/2)gt^2…(b)"
{v(t)}^2 - v0^2 = -2gy(t)…(c)"

ここで(b)"をtについて変形したら

y(t) = -(1/2)g{t - (v0/g)}^2 + (v0^2)/(2g)…(b)'''
(ただしt>0)

となります。

v0/g > 0ですから、時刻tにおける物体の上昇高度y(t)はt = v0/g のとき最大値 (v0^2)/(2g)を取ります。
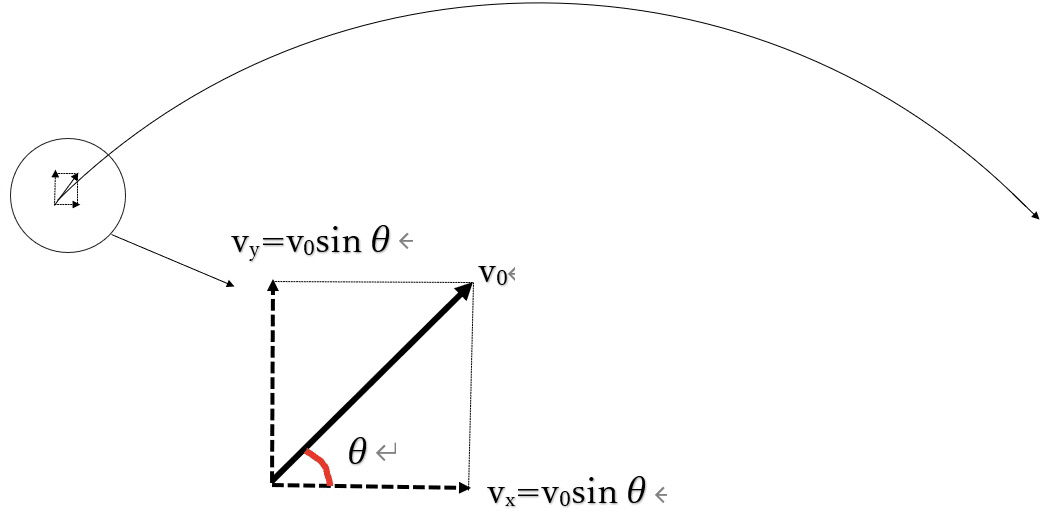
これを基にして次の[図5]に示すような鉛直投げ上げ運動を考えてみましょう。

例えば上図のように水平方向に初速度v_x[m･s^-1]、鉛直方向に初速度v_y[6･s^-1]で投げ上げる場合を考えます。このときの物体の進行方向はこの水平方向と鉛直方向の速度ベクトル和の向きとなりますから、斜め上方向になるのですね。

※ベクトルについて

ベクトルとは二次元平面座標的に見ると、ある点を原点O(0,0)と見なしたときのその他の位置を座標(x,y)として表したものになります。例えば次の図のように、OA=(4,5)、OB=(2,7)という2つの平面ベクトルを考えるものとします。このとき、ABというベクトルは点A(4,5)を基準、つまり原点O(0,0)と見なしますから、点Bの座標(2,7)からx座標を4、y座標を5だけ引くとABというベクトルを求めることが出来ます。つまり、

AB = OB - OA = AO + BO

となるのですね。

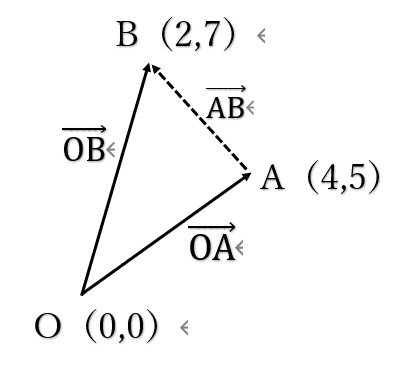
ベクトルの足し算と引き算を含む方程式は、通常の方程式と同じように計算して差し支えはありませんから、OBというベクトルは

OB = OA + AB

という形で示されます。つまりOAとABを辺とする平行四辺形の対角線が、OBというベクトルに等しくなるのですね。
なお、ベクトルの大きさは│OA│や│OB│や│AB│などとベクトルに絶対値の記号を付けた形で表され、x=(a,b)に対して

│x│ = √(a^2 + b^2)

と表現されます。

(b)'''式よりt=v_y/g[sec]のとき物体の上昇する高さy(t)は最大値y(t) = y_max
= (2v_y^2)/g[m]…(＊)を取ります。
ではこのときの水平方向の進行距離x(t)はどうなるでしょうか。
水平方向には鉛直方向と異なり、重力加速度のような加速度は働きません。つまり空気抵抗の影響を無視すれば、水平方向の物体の速さは着地するまでずっとv_x[m･s^-1]で一定なのです。ですから、物体の最上昇点における水平方向の移動距離x_maxは

x(t) = x_max = v_x･(v_y/g) = (v_x･v_y)/g …(＊＊)

となります。
ではここで、水平方向の速度ベクトルと鉛直方向の速度ベクトルの和、つまり斜め上方向の速度ベクトルの大きさ(=速さ)をv0として、この速度ベクトルが水平方向に対して成す角をθとしたとき、

v_x = v0cosθ 、 v_y = v0sinθ

となります。これを(＊)と(＊＊)に代入すると、

y_max = {2(v0sinθ)^2}/g [m]

x_max = {(v0)^2}sinθcosθ/g
= {(v0)^2}sin2θ/2g

となります。0°<θ<90°より、x_maxはθ=45°のとき最大値x_max = {(v0)^2}/2gを取ることになるのですね。このときの物体の最上昇点y_maxは、sin45°=√2/2よりy_max = (v0^2)/gとなります。
では最上昇点から着地するまでの間に物体が水平方向に移動する距離はいくらになるでしょうか。
(b)'''式から

y(t) = v0･t - (1/2)･gt^2
= -(1/2)g{t - (v0/g)}^2 + (v0^2)/(2g)
(ただしt>0)

ですから、y(t) = 0となるとき

v_y･t - (1/2)･gt^2 = 0
⇔ t(v_y - gt/2) = 0
t>0より
v_y - gt/2 = 0
∴ t = 2v_y/g = (2v0sinθ)/g

つまり、時刻t = (2v0sinθ)/gにおいて投げ上げた物体は着地するわけですね。ここでお気付きになった方もいらっしゃるかも知れませんが、これは物体が最上昇点に到達するときの時刻t = v_y/g = (v0sinθ)/gの2倍になります。
よってv_x = v0cosθで一定ですから、投げ上げ地点からから着地点まで物体が水平方向に移動する距離x0は

x0 = v_x･t0 = (v0cosθ)･(2v0sinθ)/g
= {(v0^2)sin2θ}/g

となります。つまり、θ=45°のとき、水平方向の移動距離x0は最大値(v0^2)/gを取るわけですね。

❸ 単振動

では今度は等加速度運動ではなく、加速度a(t)が時刻tの連続関数で表現される場合を考えましょう。具体的にはバネの単振動を考えることにします。
ばね定数k[N･m^-1]のバネに質量m[kg]の物体を吊るし、バネが静止する位置の位相を0として鉛直上向きの位相を正とします。このとき、バネを位相x0-xまで伸ばして物体が単振動する場合を考えます。単振動を考えるにあたっては、まず円運動について理解することが最も重要です。
単振動をする物体の位相は、円運動をする物体の水平方向または鉛直方向の座標に相当します。

●円運動

円運動においては、半径1mの円の円周上で運動する物体の速度を角速度ω[rad･s^-1]として定義しています。[rad]は「ラジアン」と読み、角度の単位を表します。π(≌3.14)[rad]=180[°]ですから、1[°]≌0.017[rad]、1[rad]≌57.3[°]です。半径1mの円の円周は2π[m]なので、単位円の円周上を運動する物体の速さを1秒あたりに増加する中心角の角度で表現しているのですね。
円運動の軌道半径をr[m]としたときの接線方向の速さv[m･s^-1]は

v = rω [m･s^-1]

と表されます。1秒あたりに増加する中心角の角度に半径をかけ合わせたら、1秒あたりに物体が進んだ距離、つまり速さvを求めることが出来るのですね。高校で習うレベルの物理では、一般的に接線方向の速さvは一定である(=等速を円運動)という前提を立てています。
さらにこのとき、物体には円軌道の中心に向かって向心力という力が働きます。この向心力を作る加速度a[m･s^-2]は

a = rω^2 [m･s^-2]…(＊)

で示されます。

[(＊)の証明]
円運動をする物体の速度ベクトルの長さ(=速さ)v[m･s^-1]は
v=rω…①
であり、この速度ベクトルは円の接線方向のベクトルである。

上図のように物体が角速度ωの円運動により、微小時間dtの間にある2点PおよびQを通過する場合を考える。この2点における速度ベクトルv_P並びにv_Qを設定すると、v_Pとv_Qのなす角度は∠POQと同じくωdtであり、点PおよびQから円の中心に向かう方向の速度ベクトルはv_Q - v_Pと表現される。
等速円運動を仮定していることから、│v_P│ = │v_Q│ = vより、点PおよびQから円軌道の中心に向かう方向の物体の(見かけ上)速さdvは
dv = │v_Q - v_P│ = vωdt = (rω)･ωdt = rω^2dt
⇔ dv/dt = rω^2
すなわち
a = rω^2
となり(＊)式は示される。 (証明終)

上の証明で難しいのは、

・v_Qを点Pまで平行移動してv_Pとv_Qのなす角度がωdtであると気付くことが出来るか

・v_Q-v_Pを点PまたはQに平行移動して、向心力に起因する円軌道の中心方向の速度ベクトルと気付くことが出来るか

の2点ですね。これは物理という学問の難しさと言うよりも、数学のベクトルという単元の難しさと言ってもいいでしょう。このa = rω^2という式、数ある物理の公式の中でも理解せずに暗記している人が意外に多いのですが、実際に証明するとなるとこんなにも難しいのですね。
さて、(＊)式はv=rωより、

a = rω^2 = (v^2)/r

とも表現されます。
向心力は加速度と同様に、円運動の軌道(円)の中心に向かって働きます。この向心力F[N]は物体の質量mと加速度の大きさaの積、つまり

F = mrω^2 = m･(v^2)/r [N]

と示されます。
ではこの円運動の基本的な考え方を基にして、物体の単振動を考えてみましょう。
まず、ばね定数k[N･m^-1]のバネに質量m[kg]の物体を吊るした場合にバネがx[m]だけ伸びたとします。このとき、バネに加わる力Fは

F = kx [N]

と示されます。Fは吊るした物体に働く重力と同じですから、重量加速度g[m･s^-2]に対して

kx = mg ∴ x = (mg)/k

と表されます。
この質量mの物体を吊るしてバネが静止する位相をx=0として考え、このx=0からバネを鉛直下向きにx0[m]だけ伸ばした後に離して、物体を単振動させる場合を考えましょう。

上図のように時刻tにおける物体の位相をx(t)として、x(0)=-x0にて物体を離します(ただしこのとき、空気抵抗による影響は無視できるものとします)。物体の位相x(t)がx(t)=x0となるとき、バネはもとの形状に戻ろうとして物体を鉛直下向きに押し返そうとする(これを復元力と呼びます)ため、位相x(t)はx0より小さくなります。x(t)=-x0となるとき、バネはやはり自身の復元力により-x0より大きくなります。このサイクルを繰り返すことで、時刻tにおける物体の位相x(t)は理論上次のようなx(t) = -x0cosωtのグラフを描きます。

これは下の[図11]のように、半径x0[m]の円軌道にて角速度ω[rad･s^-1]で円運動をする物体の位相x(t)と見なすことができるのです。

では今度は、この単振動における角速度ω[rad･s^-1]を考えてみましょう。
バネの復元力F[N]は単振動の中心、つまりバネの釣り合いの位置x(t)=0に向かって働く向心力であるとみなすことができますから、
F/m = {kx(t)}/m = (k/m)･x(t)
⇔ a = (ω^2)･x(t) = (k/m)･x(t)
すなわち ω^2 = k/mより
ω = √(k/m) [rad･s^-1] (∵ω≧0より)
となります。
これよりここで考える単振動における物体の位相x(t)は

x(t) = -x0cos{√(k/m)t} …(＊)

と表すことができます。
物体の位相(=等加速度運動でいうと、距離に相当します)を時刻tの関数で表現できましたので、ここから時刻tにおける速度v(t)と加速度a(t)を求めることができそうです。
まず位相x(t)を時刻tで微分すれば時刻tにおける物体の速度v(t)を求めることが出来ます。

v(t) = dx(t)/dt
= d(-x0cosωt)/dt = (-x0)･{d(cosωt)/dt}
= -x0･(-ωsinωt)
∴ v(t) = ωx0sinωt = ωx0sin{√(k/m)t}…(＊＊)

(※) cosωtは合成関数ですから、次のように微分します。
ωt=θと置くとdθ/dt = ω より、
d(cosωt)/dt = d(cosθ)/dt
= {d(cosθ)/dθ}(dθ/dt)
= (-sinθ)･ω = -ωsinωt

さらにこの速さv(t)を時刻tで微分すると、時刻tにおける加速度a(t)を求めることができます。

a(t) = dv(t)/dt
= d(ωx0sinωt)/dt = (ωx0)･{d(sinωt)/dt}
= (ωx0)･ωcosωt
∴ a(t) = (ω^2)･x0cosωt
= (ω^2)･x0cos{√(k/m)t}…(＊＊＊)

さらに(＊)式と(＊＊＊)より、加速度a(t)は

a(t) = -(ω^2)･x(t) = -(k/m)･x(t)

と表すことが出来ます。
(＊＊)式より、自然数n(n=1,2,3..…)に対して
ωt = {(2n-1)π}/2のとき、すなわち
t = {(2n-1)π}/(2ω)= {n-(1/2)}π√(m/k)のとき│v(t)│(=速さ)は最大値ωx0を取ります。また(＊＊＊)式より、0以上の整数nに対して
ωt = nπのとき│a(t)│(=加速度の大きさ)は最大値(ω^2)･x0を取ります。
……アレ？この│v(t)│=ωx0という式と│a(t)│=(ω^2)･x0という式、どこかで見た気がしませんか？

円運動の軌道半径r[m]、角速度ω[rad･s^-1]に対して
v=rω [m･s^-1]
a = rω^2 = (v^2)/r [m･s^-2]

そうですね。これは円運動における物体の速さと加速度の式と同じ形の式になります。ただし、上記の円運動における速さと加速度の式は円軌道のある定点のみで観測したときの速さと加速度であるのに対して、先ほどまでお話しました単振動においては(単振動を円運動と見なしたときにおける)水平方向または鉛直方向の各時刻における位相ごとの速さと加速度であるという点に注意してください。

[図12] 単振動を円運動と見なしたときの、時刻tにおける速度v(t)の経時的変化

具体的にどういうことか考えていきましょう。先ほどまで考えたバネの単振動を角速度ω=√(k/m) [rad･s^-1]、接線方向の速さv=(一定)の円運動であると見なして、鉛直方向の速度成分v(t)をグラフにプロットしていきます。この速度成分v(t)は接線方向の速さvに対してv(t) = vsinωtと見なすことができ、加えて円軌道の半径、すなわちバネの振幅はx0ですからv=ωx0となるため、v(t) = ωx0sinωtと表現することができるのです。
なお、この単振動の周期をT[sec]とすると、

v×T = 2πx0

より

T = (2πrx0)/v = (2πrx0)/(ωx0) = (2π)/ω
すなわち

T = 2π√(m/k) [sec]

と表現することができます。
① ωt = 0 すなわちt=0のとき、v(t)=0となります。
② ωt = π/4 すなわちt=π/(4ω)=T/8のとき、v(t)=v/√2となります。
③ ωt = π/2 すなわちt=π/(2ω)=T/4のとき、v(t)=v(最大)となります。
④ ωt = 3π/4 すなわちt=3π/4ω=3T/8のとき、v(t)=v/√2となります。
⑤ ωt = π すなわちt=π/ω=T/2のとき、v(t)=0となります。
⑥ ωt = (5π)/4 すなわちt=5π/(4ω)=5T/8のとき、v(t)=-v/√2となります。
⑦ ωt = 3π/2 すなわちt=3π/(2ω)=3T/4のとき、v(t)=-v(負の向きにおいて最大)となります。
⑧ ωt = 7π/4 すなわちt=7π/(4ω)=7T/8のとき、v(t)=0となります。

①～⑧をt-v(t)のグラフにプロットしていくと[図12]のようにv(t) = vsinωtのグラフを得ることができます。

○練習問題

(https://kgkrkgk.com/phys/tip09f.htm より引用)

では復習がてら、実際の入試問題で単振動の問題を見て終わりにしましょう。2009年の東京工業大学の入試問題になります。

(a) 物体が壁から離れるときの物体Bの速さv0を求めよ.

(解) エネルギー保存則より
(1/2)kl^2 = (1/2)mv0^2
∴ v0 = l√(k/m) …(答)

(a)についてはバネによる弾性エネルギーU=(1/2)kx^2をまだ説明してなかったですね。

バネによる弾性エネルギーUは、バネの弾性力F=kxをxで微分すると得られる仕事に相当します。
U = ∫Fdx = ∫(kx)dx = (1/2)kx^2

(b) 物体Aが壁から離れた直後の、バネの中点Pの速さv_Pをv0を用いて表せ.

(解) AとBの位相をそれぞれx_Aおよびx_Bとすると、その中点Pの位相x_Pは

x_P = (x_A + x_B)/2 = x_p

であり、A、B、Pの3点それぞれにおける速さv_A、v_Bおよびv_Pが

v_P = dx_P/dt
v_A = dx_A/dt = 0
v_B = dx_B/dt = v0

で表されることから、

v_P = dx_P/dt = (1/2)(dx_A/dt + dx_B/dt)
= (v_A + v_B)/2 = v0/2 …(答)

ここでv=dx/dtが出てきましたね。物体Aが壁から離れた直後を考えますからv_A = dx_A/dt = 0と見なすことができ、また(a)の結果からv_B = dx_B/dt = v0となりますから、v_p = v0/2となります。

(c) 物体Aが壁から離れる時刻をt=0とし、その後、ばねの長さが初めて自然長Lとなるときの時刻をt=t1とする。t1を求めよ。

(解) 右向きを働く力の正の方向とする。
物体Aに働くバネの弾性力はk(x_B - x_A - L)であり、物体Bに働くバネの弾性力はk{L - (x_B - x_A)}であるから、物体AとBそれぞれの加速度をaとしてAとBの運動方程式を立式すると

m･a_A = k(x_B-x_A-L) …①
m･a_B = k{L - (x_B - x_A)} …②

またx_P = (x_A + x_B)/2よりx_B = 2x_P - x_Aであるから、これを①に代入すると

m･a_A = k{2(x_P - x_A) - L}
∴ a_A = -(2k/m)(x_A - x_P - L/2) …①'

同様にしてx_A = 2x_P - x_Bであるから、これを②に代入すると

m･a_B = k{L - (x_B - x_A)}
∴ a_B = -(2k/m)(x_B - x_P - L/2) …②'

ここでAとBが作る物体系の重心の位相x_ABは

x_AB = (m･x_A + m･x_B)/(m+m)
= (x_A + x_B)/2 = x_P

となり、点Pが物体系ABの重心であることが分かる。
①'と②'より、物体AとBは(物体系の重心Pから見ると)角速度√(2k/m)の単振動をすることが分かるため、この単振動の周期Tは

T = 2π/ω = 2π√(m/2k)

よってt=0の後にバネが自然長に戻る時刻t1は
t1 = T/2 = π√(m/2k) …(答)

この問題、AとBの物体系の重心、つまり点Pを基準(=原点)と見なして単振動を考えることが出来るかがポイントになります。点Pを基準にするということは

a_A = -(2k/m)(x_A - x_P - L/2)
a_B = -(2k/m)(x_B - x_P - L/2)

というように、AとBの位相x_Aおよびx_Bから点Pの位相x_Pを差し引いて
a = -(ω^2)･x + C (x = x_A - x_P またはx = x_B - x_P 、Cは定数)の形の加速度aの式を立式することで答えに近づくことができます。
後ほど詳しく説明しますが、結論から言いますと物体Aが壁から離れるときにはバネの長さが自然長に戻ります。バネの単振動において、押し縮めた(伸ばした)バネが自然長に戻る時刻をt=0とすると物体の位相は時刻tに対してsin型の関数で表現することができ、単振動の周期をTとしたときにバネの長さが自然長に戻る時刻はt=T/2となります。単振動の周期TはT=2π/ωですから、先ほど示した運動方程式を立式すれば周期Tを求めることができますね。

(d) 時刻t=t1の後、ばねの長さが次に自然長Lになる時刻をt=t2とする。時刻t=(t1 + t2)/2におけるバネの長さL_sをLとlを用いて表せ.

(解)
t=0のとき、AとBはともに振動中心にあり、点P(=物体系ABの重心)がAとBの中点にあることから
x_A - x_P = -L/2 かつ x_B - x_P = L/2 ゆえに、単振動の振幅をCとすると

x_A - x_P = -L/2 - Csinωt …①
x_B - x_P = L/2 + Csinωt … ②

①より

v_A - v_P = d(x_A - x_P)/dt = -ωCcosωt

であり、(b)の計算過程よりt=0のときv_P = v0/2 かつ v_A = 0より、

-v0/2 = -ωC
∴ C = v0/(2ω)

ここで(c)の計算過程よりω=√(2k/m)であるから、

C = (v0/2)√(m/2k)

であり、(a)の結果からv0 = l√(k/m) ゆえに

C = (l/2)･{√(k/m)}･{√(m/2k)}
= l/2√2 …③

さらに②-①よりバネの長さx_B - x_Aは

x_B - x_A = (x_B - x_P) - (x_A - x_P)
= L/2 + Csinωt - (-L/2 - Csinωt)
= L + 2Csinωt …④

であるから、バネの長さx_B - x_Aが時刻t=t1の後で再びLとなるとき、

L + 2Csinωt = L
⇔ sinωt = 0
⇔ ωt = 0、π、2π、3π、…

すなわちωt = π、つまりt = π/ω = π√(m/2k)となるときバネの長さx_B - x_Aは再びLとなるので、(c)よりt1 = π√(m/2k)であることから

t2 = t1 + π√(m/2k) = π√(m/2k) + π√(m/2k)
= 2π√(m/2k)

よってこの単振動の周期Tに対して

(t1 + t2)/2 = {π√(m/2k) + 2π√(m/2k)}/2
= (3π/2)√(m/2k) = 3T/4

であるから、④よりt=(t1 + t2)/2のとき
L_s = x_B - x_A
= L + 2Csin(ω･3T/4)
= L + 2Csin(2π･3/4) (∵ωT = 2πより)
= L + 2Csin(3π/2)
∴ L_s = L - 2C …⑤
③よりC = l/2√2だから、これを⑤に代入すると
L_s = L - 2･l/2√2 = L - l/√2 …(答)

t=0のとき、つまり物体Aが壁から離れるタイミングではAとBはともに振動中心にある(=AとBはそれぞれの単振動における原点に相当する位置にある)こと、そして物体Aから点Pまでの距離x_A - x_Pと物体Bから点Pまでの距離x_B - x_Pがtの三角関数で表現することができることの2点に注目するのがポイントです。

x_A - x_P = -L/2 - Csinωt …①
x_B - x_P = L/2 + Csinωt … ②

時刻t=0では①と②から
x_A - x_P = -L/2
x_B - x_P = L/2
となります。バネの長さはx_B - x_Aですが、このとき
x_B - x_P - (x_A - x_P)
= x_B - x_A = L(自然長)
となります。つまり、(イメージしやすいとは思いますが)物体Aが壁から離れるときにはバネの長さは自然長に戻るということですね。さらにt=0においてはv_A = 0かつv_B = v0
= l√(m/k)であることが(a)と(b)から分かりましたから、①と②をtで微分して求めた速さにこれらを代入して単振動の振幅Cを求め、最終的にt=(t1 + t2)/2におけるバネの長さL_sを求めます。

(e) 時刻t=t2における物体Aの速さv_Aを求めよ.

(解) (d)の計算過程よりt2 = 2π√(2k/m) = Tであり、また(b)の計算過程よりt = 0のときv_A = 0であることから、求める時刻t=t2における物体Aの速さv_Aは
v_A = 0 …(答)

意外にアッサリ答えが出ちゃいましたね。(笑)もっと詳しく掘り下げて考えていくことにしましょう。
まず物体AとBの運動方程式を立式すると、

m･a_A = k(x_B-x_A-L) …①
m･a_B = k{L - (x_B - x_A)} …②

であり、①+②より

m･(a_A + a_B) = 0
∴ a_A + a_B = 0 …③

ここで点Pの位相x_Pは時刻tによらず常に

x_P = (x_A + x_B)/2

ですから、点Pの加速度a_Pは

a_P = d^2x_P/dt^2
= (1/2)･(d^2x_A/dt^2 + d^2x_B/dt^2)
= (1/2)･(a_A + a_B) = 0 (∵③より)

つまり点Pは(b)の結果から時刻t=0以降でv_P = v0/2の等速運動を行うことになります。よって(d)の計算過程より

x_A - x_P = -L/2 - (l/2√2)sinωt

ですから、この両辺をtで微分すると

v_A - v_P = -{(ωl)/2√2}cosωt
⇔ v_A = v0/2 - {(ωl)/2√2}cosωt

ここで(d)の計算過程よりt2 = 2π√(m/2k) = Tですから、t=t2のときのv_Aは

v_A = v0/2 - {(ωl)/2√2}cosωT
= v0/2 - {(ωl)/2√2}cos2π
= v0/2 - {(ωl)/2√2}
= (l/2)√(k/m) - (l/2√2)√(2k/m)
(∵(a)の結果からv0 = (l/2)√(k/m)であり、(b)の計算過程よりω = √(2k/m)より)
= (l/2)√(k/m) - (l/2)√(k/m)
= 0 …(答)

となるわけですね。

(f) 時刻t=t2に、物体Bに水平方向の撃力を加えたところ、ばねの中点Pが静止した。撃力とは極めて短い時間に物体に作用する力である。撃力の力積の大きさIをv0を用いて表せ.

(解) バネの中点Pが静止するとき、物体系AとBの運動量が0となる。物体Bの速さv_Bは、(d)の計算過程よりt2=Tであり時刻t=0のときv_B = v0であるから、時刻t=t2においてv_B = v0となる。よって物体系の運動量はmv0であるから、与えた撃力の力積の大きさIは
I = mv0 …(答)

ここでの解答のポイントはズバリ、「バネの中点Pが静止する ⇔ 物体系ABの運動量が0となる」という点に気付けるか否かということですね。一応復習しておきますと、運動量pは物体の質量mと速さvの積で表現されます。

運動量p = mv = madt = Fdt

問題文では既にバネの質量は無視出来るほど小さいことが前提条件に挙げられていますから、バネの運動量は無視できます。つまり、物体AとBの運動量の和を物体系AとBの運動量と見なして差し支えないということですね。
(d)の計算過程よりt2=Tであることが分かりましたから、t=t2のときのAとBそれぞれの速度v_Aおよびv_Bはt=0のときの速度に等しくなります。つまり、(b)の計算過程よりv_A = 0、v_B = v0ですね。これより、物体系ABの運動量p_ABは

p_AB = m･v_A + m･v_B= m･0 + m･v0
= mv0

となります。このp_ABを0にする(=ばねの中点Pを静止させる)には、同じ大きさの運動量を持つ撃力を物体系ABの進行方向と反対側に加えれば良いと考えることができます。ですから、求める撃力の大きさIは
I = mv0 …(答)
となるわけですね。

ということで、本日は等加速度運動やバネの単振動を微積を使って考えるということをテーマにお話しました。特にバネの単振動の問題では先ほど見た練習問題のように、計算過程で三角関数の微分積分が必須となりますから、前回お話しました数学Ⅲの微分積分のお話も是非見直してみてください。

それではまた次回もよろしくお願いしますm(_ _)m