
【Python】黒毛和牛の反芻時間に影響を与える要因、反芻時間の予測可能性について分析、検討してみた
※このブログはAidemy Premiumのカリキュラムの一環で、受講修了条件を満たすために公開しています。
はじめに
近年、コスト削減や人材不足を補うため畜産業界でもIoTデバイスやそのデータの活用技術が普及してきています。しかし多くのデータを収集できるようにはなったものの、活用面ではまだまだ限定的でデータの多くが可能性のまま残されているのが現状です。

「反芻時間」は活用の可能性を秘めたデータの1つです。牛には4つの胃袋があります。その中の1番目の胃袋(第一胃)は発酵タンクの役割をしており、牛は一度食べた餌を第一胃の中で発酵させながら、時折吐き戻して咀嚼し、唾液と混ぜて再び飲み込みます。この行動を「反芻」と言い、反芻を行う事で牛は第一胃における発酵を促します。この反芻時間は食欲(健康)の指標であると同時に餌(成分や量)の指標にもなります。健康で食欲旺盛ならたくさん食べてたくさん噛みます。また人がパンを食べるときと繊維質なきんぴらごぼうを食べるときで咀嚼の回数が違うように、食べる物の性質でも反芻の時間は異なります。そのため、反芻時間とそれに影響を与える要因との関係を明らかにすることで健康チェックや餌がその牛に合っているかを評価できる可能性があります。一方で反芻時間に影響を与える要因(気温、湿度、体格、性別、月齢、餌の成分、餌の量…..)は数多く、また個体差も大きい事がわかっているため反芻時間だけを見て何かを評価する事はできません。
そこで統計学的な回帰分析や機械学習を利用して、ある状況下における個体毎の「あるべき反芻時間」が算出できれば、「実際の反芻時間」と「あるべき反芻時間」の差が大きな個体を何か問題がある個体と判定できるのではないかと考えました。今回はそのために必要な「あるべき反芻時間」を算出する事に挑戦してみました。
なお、牛には牛乳を得るための搾乳牛(ホルスタイン牛、ジャージー牛など)や肉を得るための肥育牛(ホルスタイン牛、交雑種、和牛)などがいますが、今回は肥育牛の中の黒毛和牛(去勢)の反芻時間について分析しました。


実行環境
Google Claboratory
Python version: 3.10.12
OS: linux
生データ
(71076×24)のExcelデータ
・2021/8/1~2022/8/31の期間で個体毎に24時間の集計値として記録されています。
・24時間の集計値であり、日付けが変われば別のデータとして記録されるため、日付けの異なる同じ個体のデータが重複して存在します。
・期間の途中から首輪を装着した個体や、出荷されて居なくなった個体を含んでいます。
・今回はIoTデバイスで収集できるデータとその管理ソフトに入力されたデータの抽出のため、餌のデータは含まれません。
・記録項目:農家名、測定日、気温(平均、最高、最低、標準偏差(SD))、湿度(平均、最高、最低、SD)、不快指数(THI)(平均、最高
、最低、SD)、牛番号、個体識別番号、性別、牛群名、出生日、月齢、動態時間、横臥時間、起立時間、起立反芻時間、横臥反芻時間、合計時間
※THIは気温と湿度から算出されます
※気候に関するデータのSDは「最高気温‐最低気温」と同じように寒暖差のような気候の変動を示すと考えます
※合計時間=起立反芻時間+横臥反芻時間

データの前処理①
Excelデータの取り込み
#Excelデータの読み込み
from google.colab import drive
drive.mount('/content/drive')
import pandas as pd
import numpy as np
df = pd.read_excel('/content/drive/MyDrive/rumnation data/20210801_20220831 反芻全頭.xlsx',sheet_name='雌全頭',header=0,engine='openpyxl')不要な行の削除①
・雌牛データの削除
雌牛は性周期によって反芻時間が極端に変化するため、今回の分析からは除きます。
・空欄を含む行の削除(4行) リストワイズ削除
#不要な行の削除
#雌の行を削除
f_index = df[df['sex']=='メス'].index
df.drop(f_index,inplace=True)
#NAN含む4行削除
df=df.dropna()カラム名の変更
後程のMtplotlibで日本語表記は文字化けするため英語表記に変更しました。
#グラフで日本語表記が不安定なのでカラム名を英語に変更
new_columns = ['Date','ave_tem','ave_hum','ave_THI','SD_tem','SD_hum','SD_THI','max_tem','max_hum','max_THI','min_tem','min_hum','min_THI','ID','month_age','act','lay','stand','rum_stand','rum_lay','rum_sum']
df.columns=new_columns不要な列の削除
・農場名
今回のデータは1農場のデータの為、すべての行で共通なため削除します。
・計測日
今回のデータでは日付け自体に意味はなく、月齢の列があるため削除します。
・牛番号
個体識別番号と同じ意味の為、個体識別番号を残して牛番号は削除します。
・牛群名
牛舎の名前が記録されていますが、飼い主からラベリングが不適当であった旨の報告を受けているため削除します。
・出生日
計測日と同様、月齢の列があるため削除します。
#不要な列の削除
#農場名、sex、牛群名、牛番号、出生日を削除
drop_col = ['農場名','sex','牛群名','牛番号','出生日']
df.drop(drop_col,axis=1,inplace=True)カラム名の変更
後程のMtplotlibで日本語表記は文字化けするため英語表記に変更しました。
#グラフで日本語表記が不安定なのでカラム名を英語に変更
new_columns = ['Date','ave_tem','ave_hum','ave_THI','SD_tem','SD_hum','SD_THI','max_tem','max_hum','max_THI','min_tem','min_hum','min_THI','ID','month_age','act','lay','stand','rum_stand','rum_lay','rum_sum']
df.columns=new_columns不要な行の削除②
・異常な反芻時間の削除(外れ値の削除) リストワイズ削除
今回は健康な牛のデータを扱うため、病気による反芻時間の低下やデバイスの電池交換作業に伴う異常値等を除きます。すべての期間の平均値±2SDを上回る/下回る反芻時間を示した行のデータはすべて削除します。(平均値±2SDが反芻時時間の異常を判別する最適な範囲である根拠はありません。獣医療域では血液検査における健康牛の範囲が平均値±2SDに設定されている事が多いため、今回もその設定に倣いました。)
#平均値±2SDを逸脱する反芻時間を持つ行を削除
#'rum_stand','rum_lay','rum_sum'について平均値±2SDを求める
print(np.std(df[rum]))
print(np.mean(df[rum])-2*(np.std(df[rum])))
print(np.mean(df[rum])+2*(np.std(df[rum])))
#rum_sum mean±2SD を超える行を削除
df = df.query('rum_sum >= 132.9024305347534')
df = df.query('rum_sum <= 417.42071830340115')データの可視化
統計量の確認
平均気温 最小値:-0.1℃ 最大値30.3℃
月齢 最小値:11.3ヶ月齢 最大値:32.1ヶ月齢
最も早い牛は11.3ヶ月齢にデバイスを装着され、最も長く装着された牛は32.1ヶ月齢まで着けていました。デバイスを外された時期はお肉になるために出荷された時期と一致します。(短い命です。)
合計反芻時間 最小値:120分/日 最大値440分/日
平均:273.1分/日 標準偏差:65.4分/日
0分はデバイスに何らかの問題が発生していたと考えられます。電池切れや牛から外れていた等。平均±SDが約210~340分/日の範囲を示しました。全体の70%のデータ(牛)をカバーする値なのでほぼ健康な普通の牛と考えられますが結構な幅があります。このことからも単純に数字を見ただけでは反芻時間から健康か不健康かを判断する事が難しいとわかります。
#統計量
display(df.describe())

ヒートマップ
当然ですが、気象関係同士では相関係数が高い事がわかります。
また、活動と反芻の分野の中にも相関係数が高い項目がありますが、それについては相関行列を示しながら後述します。齢(月齢)はどの項目に関しても特別高い相関は示しませんでした。
import seaborn as sns
sns.heatmap(df[['ave_tem', 'ave_hum', 'ave_THI', 'SD_tem', 'SD_hum', 'SD_THI',
'max_tem', 'max_hum', 'max_THI', 'min_tem', 'min_hum', 'min_THI', 'ID',
'month_age', 'act', 'lay', 'stand', 'rum_stand', 'rum_lay', 'rum_sum']].corr(),vmax=1,vmin=-1,annot=True,fmt='.2g')
sns.set(rc={"figure.figsize": (20, 40)})
散布図行列
齢(月齢)、活動、反芻に関して、気象関係と強い相関を示すものはありませんでした。月齢と活動や反芻に関しても同様です。一方、活動と反芻に関しては一部で負の相関を示すものがあります。これは24時間を活動(動態、起立、横臥)と反芻(起立反芻、横臥反芻、反芻合計)で分け合っているため、トレードオフの関係が成り立ってしまっているためと考えられます。
import matplotlib.pyplot as plt
sns.pairplot(df)
plt.tight_layout()
plt.show()
正規性の確認
目的変数となる反芻時間の正規性を確認しました。ヒストグラムはほぼ釣り鐘型で正規性があると判断しました。
fig = plt.figure()
ax2 = fig.add_subplot(1,1,1)
ax2.hist(df['rum_lay'],alpha=0.5,bins=50,label='rum_lay')
ax2.hist(df['rum_stand'],alpha=0.5,bins=50,label='rum_stand')
ax2.hist(df['rum_sum'],alpha=0.5,bins=50,label='rum_sum')
plt.xlabel("time(min/day)")
plt.ylabel('cow-day')
plt.legend(loc='upper right')
plt.subplots_adjust(wspace=0.5)
plt.show()
データの前処理②
変数の絞り込み(多重共線性の回避)
活動時間については反芻時間とトレードオフの関係にあるため、今回は変数として使用しないことにしました。
気候のデータについて、THIは気温と湿度から算出される指標の為、今回は使用しないことにしました。
3種類の反芻時間(起立、横臥、合計)に関して、一般的に寝ながら反芻している牛ほどリラックスしており健康と言われていますが、一方で今回使用したデバイスでは立って反芻している時間には餌を食べている時間も含まれてしまっているため、起立反芻時間が長い牛は健康でよく食べる牛とみることもできます。どちらを健康のバロメーターとするべきか判断できないので今回は合計反芻時間を目的変数とすることにします。
月齢はそのまま採用しました。
標準化
気温と反芻時間など単位が異なる変数を扱うため、標準化して単位をないものとします。
#標準化
from sklearn import preprocessing
from sklearn.preprocessing import StandardScaler
stds = StandardScaler()
# 標準化するカラム
scaling_columns = ['ave_tem','ave_hum','ave_THI','SD_tem','SD_hum','SD_THI','max_tem','max_hum','max_THI','min_tem','min_hum','min_THI','month_age','act','lay','stand','rum_stand','rum_lay','rum_sum']
#標準化
sc = stds.fit(df[scaling_columns])
#標準化したカラムのみ元のデータフレームに戻す
scaled_df = pd.DataFrame(sc.transform(df[scaling_columns]), columns=scaling_columns, index=df.index)
#'ID'戻す
scaled_df['ID'] = df['ID']統計学的アプローチ①
重回帰分析①
まず多重共線性を許してすべての気象データと月齢を目的変数に線形回帰を行いました。
yyplotで残差の正規性が認められなかったのでモデルに関する検定は参考にならない事がわかります。また決定係数も0.044と非常に小さく、検定以前にモデルとして全く意味をなしていない事がわかります。
寄与率を参考に多重共線性を排除した変数で再度、重回帰を行います。採用する変数は最低気温、最低湿度、月齢です。p値が高い物もありますが、残差の正規性がない事もあり、目をつぶります。
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score, mean_absolute_error,mean_squared_error
# データの分割
df_X = scaled_df[['ave_tem', 'ave_hum', 'SD_tem', 'SD_hum',
'max_tem', 'max_hum', 'min_tem', 'min_hum',
'month_age']]
df_y = scaled_df['rum_sum']
# モデルの構築
model = LinearRegression()
# モデルの学習
model.fit(df_X,df_y)
#Xに対する推測結果
pred_y = model.predict(df_X)
print('決定係数(r2):{}'.format(round(r2_score(df_y, pred_y),3)))
print('平均誤差(MAE):{}'.format(round(mean_absolute_error(df_y, pred_y),3)))
print('RMSE:{}'.format(round(np.sqrt(mean_squared_error(df_y, pred_y)),3)))
#予測実測プロットの作成
plt.figure(figsize=(6,6))
plt.scatter(df_y, pred_y,color='blue',alpha=0.3)
y_max_ = max(df_y.max(), pred_y.max())
y_min_ = min(df_y.min(), pred_y.min())
y_max = y_max_ + (y_max_ - y_min_) * 0.1
y_min = y_min_ - (y_max_ - y_min_) * 0.1
plt.plot([y_min , y_max],[y_min, y_max], 'k-')
plt.ylim(y_min, y_max)
plt.xlim(y_min, y_max)
plt.xlabel('rum_sum(observed)',fontsize=20)
plt.ylabel('rum_sum(predicted)',fontsize=20)
plt.legend(loc='best',fontsize=15)
plt.title('yyplot(rum_sum)',fontsize=20)
plt.savefig('yyplot.png')
plt.show()
print('回帰係数:',round(model.intercept_,3))
#回帰係数を格納したpandasDataFrameの表示
df_coef = pd.DataFrame({'coefficient':model.coef_.flatten()}, index=df_X.columns)
#グラフの作成
x_pos = np.arange(len(df_coef))
fig = plt.figure(figsize=(6,6))
ax1 = fig.add_subplot(1, 1, 1)
ax1.barh(x_pos, df_coef['coefficient'], color='b')
ax1.set_title('coefficient of variables',fontsize=18)
ax1.set_yticks(x_pos)
ax1.set_yticks(np.arange(-1,len(df_coef.index))+0.5, minor=True)
ax1.set_yticklabels(df_coef.index, fontsize=14)
ax1.set_xticks(np.arange(-3,4,2)/10)
ax1.set_xticklabels(np.arange(-3,4,2)/10,fontsize=12)
ax1.grid(which='minor',axis='y',color='black',linestyle='-', linewidth=1)
ax1.grid(which='major',axis='x',linestyle='--', linewidth=1)
plt.savefig('coef_sklearn.png',bbox_inches='tight')
plt.show()
import statsmodels.api as sm
df_X = sm.add_constant(df_X)
model = sm.OLS(df_y, df_X)
result = model.fit()
print(result.summary())

重回帰分析②
上記の結果から最低気温、最低湿度、月齢の3つの変数で重回帰分析を行いました。前回同様、残差に正規性は認められませんでした。また決定係数も低く、モデルとして機能していません。
# データの分割
df_X = scaled_df[['min_hum','min_tem',
'month_age']]
df_y = scaled_df['rum_sum']
# モデルの構築
model = LinearRegression()
# モデルの学習
model.fit(df_X,df_y)
#Xに対する推測結果
pred_y = model.predict(df_X)
print('決定係数(r2):{}'.format(round(r2_score(df_y, pred_y),3)))
print('平均誤差(MAE):{}'.format(round(mean_absolute_error(df_y, pred_y),3)))
print('RMSE:{}'.format(round(np.sqrt(mean_squared_error(df_y, pred_y)),3)))
#予測実測プロットの作成
plt.figure(figsize=(6,6))
plt.scatter(df_y, pred_y,color='blue',alpha=0.3)
y_max_ = max(df_y.max(), pred_y.max())
y_min_ = min(df_y.min(), pred_y.min())
y_max = y_max_ + (y_max_ - y_min_) * 0.1
y_min = y_min_ - (y_max_ - y_min_) * 0.1
plt.plot([y_min , y_max],[y_min, y_max], 'k-')
plt.ylim(y_min, y_max)
plt.xlim(y_min, y_max)
plt.xlabel('rum_sum(observed)',fontsize=20)
plt.ylabel('rum_sum(predicted)',fontsize=20)
plt.legend(loc='best',fontsize=15)
plt.title('yyplot(rum_sum)',fontsize=20)
plt.savefig('yyplot.png')
plt.show()
print('回帰係数:',round(model.intercept_,3))
#回帰係数を格納したpandasDataFrameの表示
df_coef = pd.DataFrame({'coefficient':model.coef_.flatten()}, index=df_X.columns)
#グラフの作成
x_pos = np.arange(len(df_coef))
fig = plt.figure(figsize=(6,6))
ax1 = fig.add_subplot(1, 1, 1)
ax1.barh(x_pos, df_coef['coefficient'], color='b')
ax1.set_title('coefficient of variables',fontsize=18)
ax1.set_yticks(x_pos)
ax1.set_yticks(np.arange(-1,len(df_coef.index))+0.5, minor=True)
ax1.set_yticklabels(df_coef.index, fontsize=14)
ax1.set_xticks(np.arange(-3,4,2)/10)
ax1.set_xticklabels(np.arange(-3,4,2)/10,fontsize=12)
ax1.grid(which='minor',axis='y',color='black',linestyle='-', linewidth=1)
ax1.grid(which='major',axis='x',linestyle='--', linewidth=1)
plt.savefig('coef_sklearn.png',bbox_inches='tight')
plt.show()
import statsmodels.api as sm
df_X = sm.add_constant(df_X)
model = sm.OLS(df_y, df_X)
result = model.fit()
print(result.summary())

データの前処理③
変数の正規性の確認
月齢は正規性であると判断しました。
最低湿度は99.9%が異常に突出しており外れ値の可能性があります。
最低気温には正規性が認められませんでした。
#変数の正規性確認
fig = plt.figure(figsize=[10,4.2])
ax1 = fig.add_subplot(1,3,1)
ax2 = fig.add_subplot(1,3,2)
ax3 = fig.add_subplot(1,3,3)
ax1.hist(df['min_hum'],alpha=0.5,bins=50,label='min_hum')
ax2.hist(df['min_tem'],alpha=0.5,bins=50,label='min_tem')
ax3.hist(df['month_age'],alpha=0.5,bins=50,label='month_age')
plt.subplots_adjust(wspace=0.5)
plt.show()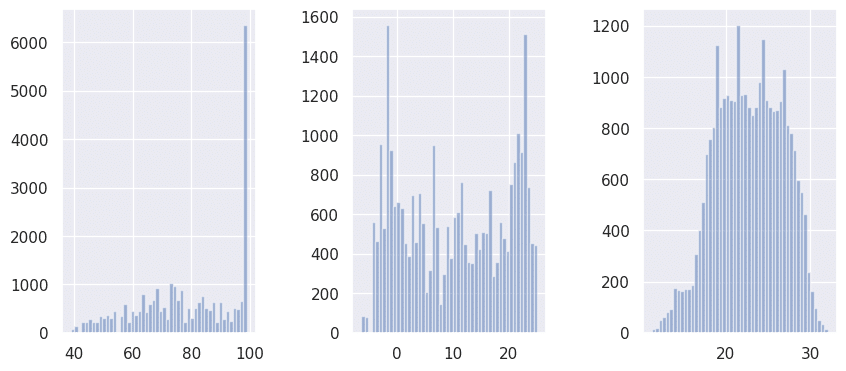
最低湿度の外れ値を含む行削除 リストワイズ
最低湿度は99.9%が異常な突出は計測器への露滴の付着等の可能性があるため90%以上の行は削除します。
#最低湿度90%以上を削除
f_index = df[df['min_hum']>=90].index
df.drop(f_index,inplace=True)変数の対数変換
残差が正規性を示しやすいように最低気温を対数化してみます。マイナスの値も取るため、最も低い日の-6.3℃を+にするために10を加えた後に対数変換しました。
#log(最低気温+10)
df['min_tem']=df['min_tem']+10
df['min_tem'] = np.log(df[['min_tem']])正規性の再確認
最低気温に関しては正規化しませんでしたが、最低湿度は正規性があるとも読めるヒストグラムになりました。

標準化
各処理の後、再度標準化しました。
統計学的アプローチ②
重回帰分析③
準備した変数で再度重回帰分析を実施しました。決定係数は0.05で低いままです。残差の正規性もありません。


多項式回帰分析
重回帰分析用に用意した変数で多項回帰分析を実施しました。
決定係数0.057で重回帰分析と大差ありませんでした。
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.preprocessing import PolynomialFeatures
df_X = scaled_df[['min_tem','min_hum','month_age']]
df_y = scaled_df['rum_sum']
# 2次元の特徴量に変換
polynomial_features= PolynomialFeatures(degree=2)
x_poly = polynomial_features.fit_transform(df_X)
# y = b0 + b1x + b2x^2 の b0~b2 を算出
model = LinearRegression()
model.fit(x_poly, df_y)
y_pred = model.predict(x_poly)
# 評価
rmse = np.sqrt(mean_squared_error(df_y, y_pred))
r2 = r2_score(df_y, y_pred)
print(f'rmse : {rmse}')
print(f'R2 : {r2}')
統計学的アプローチのまとめ
今回、統計学的アプローチでは有意なモデルを得ることはできませんでした。選択する必要な程のモデルが用意できればRidgeやLassoなども試せたかと思いますが、今回用意した変数では有用なモデルが得られそうになかったため、統計学的アプローチから機械学習に切り替えてみることにしました。
機械学習アプローチ
決定木
from sklearn import tree
from sklearn.tree import DecisionTreeRegressor
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
from sklearn.metrics import r2_score
df_X = scaled_df[['max_hum','min_tem',
'month_age']]
df_y = df['rum_sum']
train_X, test_X, train_y, test_y, = train_test_split(df_X, df_y, test_size=0.3, random_state=42)
clf = tree.DecisionTreeRegressor(max_depth=3)
model = clf.fit(train_X, train_y)
predicted = model.predict(test_X)
def True_Pred_map(pred_df):
RMSLE = np.sqrt(mean_squared_error(pred_df['true'], pred_df['pred']))
R2 = r2_score(pred_df['true'], pred_df['pred'])
plt.figure(figsize=(8,8))
ax = plt.subplot(111)
ax.scatter('true', 'pred', data=pred_df)
ax.set_xlabel('True Value', fontsize=15)
ax.set_ylabel('Pred Value', fontsize=15)
ax.set_xlim(pred_df.min().min()-0.1 , pred_df.max().max()+0.1)
ax.set_ylim(pred_df.min().min()-0.1 , pred_df.max().max()+0.1)
x = np.linspace(pred_df.min().min()-0.1, pred_df.max().max()+0.1, 2)
y = x
ax.plot(x,y,'r-')
plt.text(0.1, 0.9, 'RMSLE = {}'.format(str(round(RMSLE, 5))), transform=ax.transAxes, fontsize=15)
plt.text(0.1, 0.8, 'R^2 = {}'.format(str(round(R2, 5))), transform=ax.transAxes, fontsize=15)
pred_df = pd.concat([test_y.reset_index(drop=True), pd.Series(predicted)], axis=1)
pred_df.columns = ['true', 'pred']
True_Pred_map(pred_df)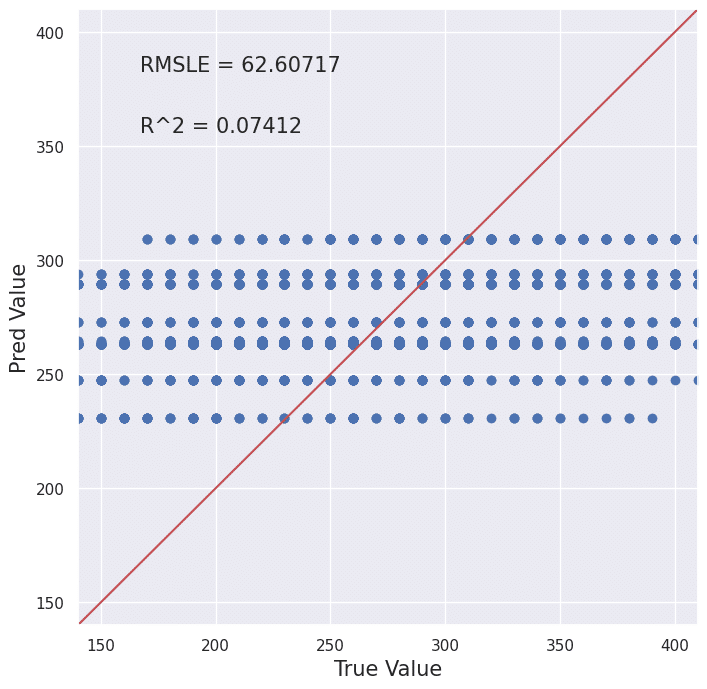
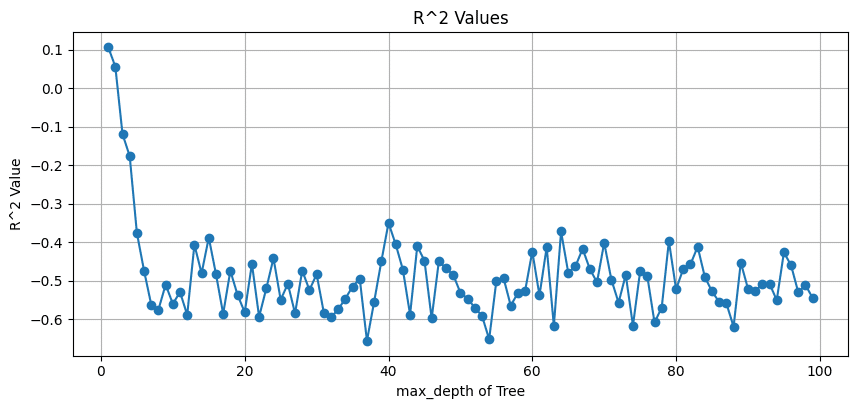
決定木の本数を100までfor文で確認
結果からランダムフォレストは実施しないことにしました。
from sklearn import tree
from sklearn.tree import DecisionTreeRegressor
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
from sklearn.metrics import r2_score
df_X = scaled_df[['max_hum','min_tem',
'month_age']]
df_y = df['rum_sum']
train_X, test_X, train_y, test_y, = train_test_split(df_X, df_y, test_size=0.3, random_state=42)
R2_list = []
count = []
for i in range(1, 100):
clf = tree.DecisionTreeRegressor(max_depth=i)
model = clf.fit(train_X, train_y)
predicted = model.predict(test_X)
pred_df = pd.concat([test_y.reset_index(drop=True), pd.Series(predicted)], axis=1)
pred_df.columns = ['true', 'pred']
R2 = r2_score(pred_df['true'], pred_df['pred'])
R2_list.append(R2)
count.append(i)
fig = plt.figure(figsize=[10,4.2])
plt.plot(count, R2_list, marker="o")
plt.title("R^2 Values")
plt.xlabel("max_depth of Tree")
plt.ylabel("R^2 Value")
plt.grid(True)
勾配木ブースティング
決定係数:0.097
MAE:51.1
#勾配木ブースティング(GBDT)
from sklearn.ensemble import GradientBoostingRegressor
GBDT = GradientBoostingRegressor()
GBDT.fit(train_X, train_y)
pred_GBDT = GBDT.predict(test_X)
r2_GBDT = r2_score(test_y, pred_GBDT)
mae_GBDT = mean_absolute_error(test_y, pred_GBDT)
print("R2 : %.3f" % r2_GBDT)
print("MAE : %.3f" % mae_GBDT)
# 変数重要度
print("feature_importances = ", GBDT.feature_importances_)
fig = plt.figure(figsize=[10,4.2])
plt.xlabel("pred_GBDT")
plt.ylabel("y_test")
plt.scatter(pred_GBDT, test_y)
plt.show()
サポートベクターマシーン(カーネル関数:linear)
決定係数:0.062
MAE:51.9
from sklearn.svm import SVR
# モデルの学習
SVR = SVR(kernel='linear', C=1, epsilon=0.1, gamma='auto')
SVR.fit(train_X, train_y)
# 回帰
pred_SVR = SVR.predict(test_X)
# 評価
# 決定係数(R2)
r2_SVR = r2_score(test_y, pred_SVR)
# 平均絶対誤差(MAE)
mae_SVR = mean_absolute_error(test_y, pred_SVR)
print("R2 : %.3f" % r2_SVR)
print("MAE : %.3f" % mae_SVR)
# 回帰係数
print("Coef = ", SVR.coef_)
fig = plt.figure(figsize=[10,4.2])
plt.xlabel("pred_SVR")
plt.ylabel("test_y")
plt.scatter(pred_SVR, test_y)
plt.show()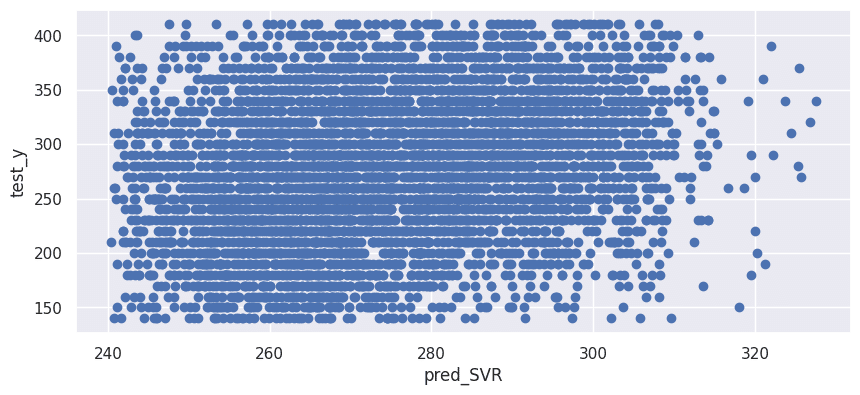
サポートベクターマシーン(カーネル関数:poly)
決定係数:0.077
MAE:51.52
# モデルの学習
SVR = SVR(kernel='poly', degree=3, coef0=1, C=5)
SVR.fit(train_X, train_y)
# 回帰
pred_SVR = SVR.predict(test_X)
# 評価
# 決定係数(R2)
r2_SVR = r2_score(test_y, pred_SVR)
# 平均絶対誤差(MAE)
mae_SVR = mean_absolute_error(test_y, pred_SVR)
print("R2 : %.3f" % r2_SVR)
print("MAE : %.3f" % mae_SVR)
fig = plt.figure(figsize=[10,4.2])
plt.xlabel("pred_SVR")
plt.ylabel("test_y")
plt.scatter(pred_SVR, test_y)
plt.show()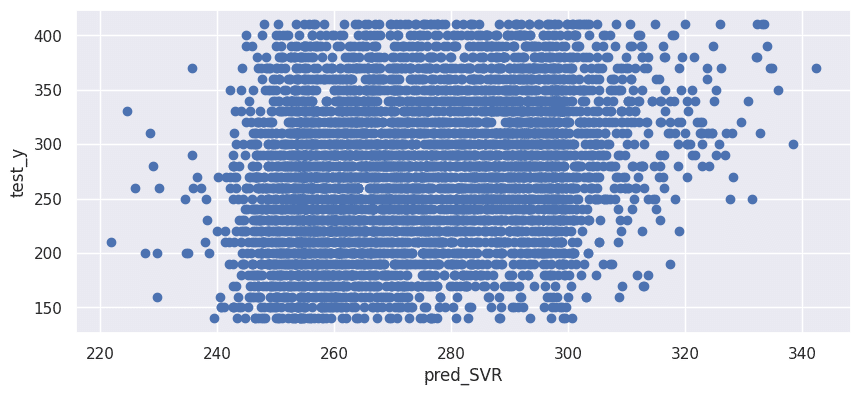
機械学習まとめ
決定係数等は統計学的アプローチをした時よりも改善される事もありましたが、モデルとして有用性があるレベルの物ではありませんでした。その理由として、餌の情報や体格など重要な変数が欠けている可能性があります。また、この調査の目的は、ある条件下である個体が示す正常な反芻時間を推測する事でした。現状ではこれ以上説明変数を増やすことはできないため、個体としてダミー変数No10の1頭について統計学的アプローチ、機械学習アプローチをとってみることにします。
個体データでの統計学的アプローチ
ID = 10の個体を抽出して新しいdataframeとします。数値は既に標準化されているのでそのまま使用します。
Dateを残した状態で牛群全体のデータを扱った時と同様にデータクレンジングを行いました。
IDをダミー変数化して呼び出しやすくしました。ここから先は例としてID_10の個体のデータを分析します。
from sklearn.preprocessing import LabelEncoder
le = LabelEncoder()
df['ID']=le.fit_transform(df['ID'])
#例としてID_10呼び出し
ID_10 = df.query('ID==10')さらに呼び出したID_10のデータフレームに前日の反芻合計時間のデータを組み込みました。
#日付順にソート
s_ID_10 = ID_10.sort_values('Date')
#前日のrum_sum列挿入
ID_10_rum_sum= s_ID_10['rum_sum'].shift()
s_ID_10["rum_sum_lag1"] = ID_10_rum_sum
ID_10 = s_ID_10.drop(s_ID_10.index[0])重回帰分析
牛群全体のデータの時と同様に重回帰分析を行いました。説明変数に前日の反芻時間'rum_sum_lag1'が追加されたことだけが変更点です。
決定係数:0.21
MAE:0.72


多項式回帰分析
決定係数:0.32
RMSE:0.83
統計学的アプローチのまとめ
個体に分けてもイマイチでした。機械学習に進みます。
個体データでの機械学習アプローチ
決定木

勾配木ブースティング
決定係数:‐0.25
MAE:0.87

SVM (カーネル関数:linear)
決定係数:0.058
MAE:0.73

SVM(カーネル関数:poly)
決定係数:‐0.26
MAE:0.81

機械学習のまとめ
個体に分けて機械学習をしてもイマイチでした。こうなるとやはり重大な変数が欠けている可能性が高いと考えます。餌と体格のデータを追加調査して再度チャレンジする必要があります。
今後の展望
今回の調査の最終的なゴールは反芻時間から個体の体調を判断するために、ある環境下におけるその個体の正常な反芻時間を予測する事でした。
そのために当初は回帰分析による正常な反芻時間の予測を目指していました。しかし今回データ解析を行う中で本当に必要な事はピンポイントな正常値を求める事ではなく、正常な範囲を得る事であると思考を立ち返らせることができました。時系列解析によって反芻時間の正常範囲を算出できるか試してみる必要があります。しかし今回の解析で明らかになったように、重要な変数を欠いたままでは時系列解析の精度も上がらない可能性が高いため、やはり追加の調査が必要です。
また成長に伴った反芻時間の変化の概形(主成分分析を利用して気温等の環境の影響を小さくした反芻時間をy軸に、月齢をx軸に取ったグラフ)と枝肉成績(枝肉の重さやサシの入り方(A5など))を紐づけて、どのような反芻の推移を目指したら健康で良い肉の牛になるかの指標を求める事も有用かもしれません。



