京大入試数学でコンスタントに8割以上得点するための勉強法
オンライン塾agora🏦です。'22年11月より新規生徒の募集を開始しました。体験or入会希望の方は googleフォーム / 公式LINE にてご連絡をお待ちしております。
agora(アゴラ)は、京大生・京大卒の起業家、研究者、Software Engineer、外資系戦略コンサルティングファーム内定者およびデザイナー等を中心に運営しているdiscordベースのオンライン塾です。'20,'21年度合わせて、東大1名(/1名)、京大4名(/7名)、阪大2名(/2名)、国公立医学科1名(/2名)の合格実績があります。
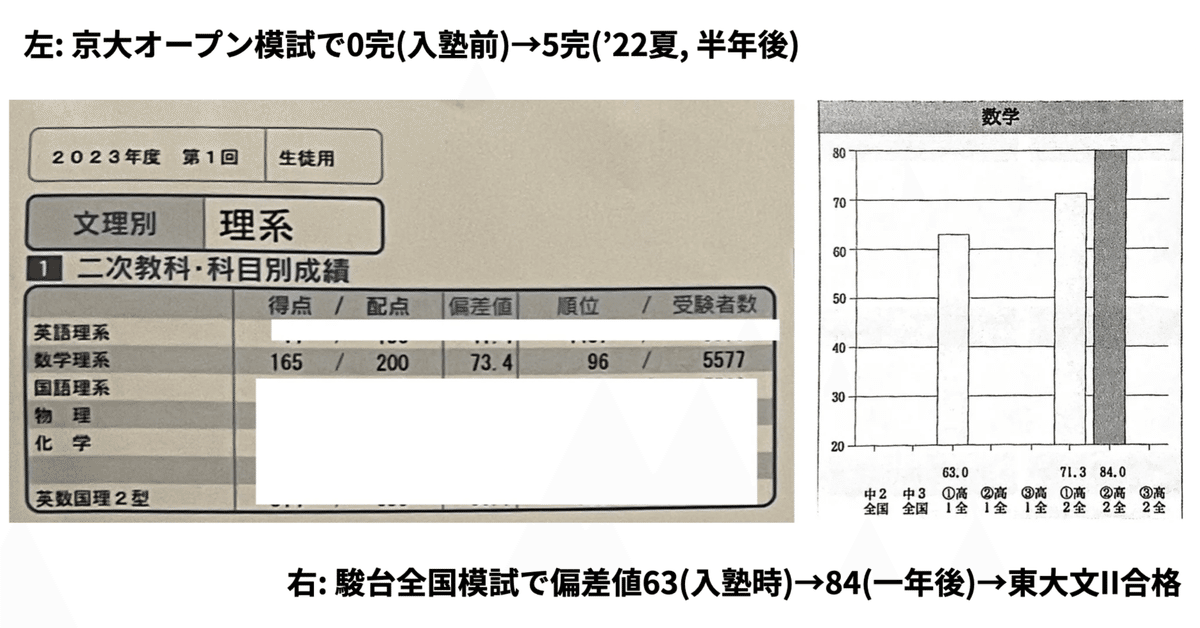
さて、カバー画像の通り、担当生徒の成績を
京大オープン模試で0完(入塾前)→5完(’22夏, 半年後)
駿台全国模試で偏差値63(入塾時)→84(一年後)→東大文II合格
まで伸ばし、自身も京大入試の理系数学で9割以上得点して合格した数学の勉強法を紹介します。
はじめに
京大数学は、他大入試と比べて大きく2つの特徴があります:
・ 典型問題は少なく「初見の問題」が殆どを構成する
・ 答案が全て記述式であり「論理」が厳しくみられる
ゆえに、「典型問題の解き方」を学ぶことに加えて、下記が必要になります:
「初見の問題」を解くために
① 「解き方」だけでなく「考え方」も学ぶ必要がある(Stage2)
論理的に正しい答案を書くために
② 「論理」や「答案の型」を学ぶ必要がある(Stage1α)
また「典型問題」についても、試験時間内に「確実に」解くために
③ 典型問題の「体系化」をする必要がある(Stage1)
しかし、多くの塾や学校では、上記 ① ~ ③ が教えられていません。
京大受験生が抱える以下 ①' ~ ③' の悩みは、このことに起因します。
①'「知っている問題は解けるが、初見の問題は解けない」
②'「答えは合っているのに、大幅に減点されてしまう」
③'「知っている問題も、試験時間内に方針が思いつかない」
次章では、上記 ①~③ を含む勉強法を説明する形でagora独自カリキュラムを紹介いたします。
agora独自カリキュラム
Stageとは
agoraでは、入試数学の学習段階を以下のように分けています:
Stage0: 定義や定理を学ぶ段階
Stage1: 典型問題の「解き方」を学ぶ段階
Stage2: 初見の問題の「考え方」を学ぶ段階
各Stageは2つに分けられ、それぞれ下記のように修了基準を設定しています:
Stage0: 教科書の章末問題を解くことができる
Stage0α: 定義や定理について深く理解している
Stage1: 典型問題を解くことができる
Stage1α: 論理的に正しい答案を書くことができる
Stage2: 初見の標準問題を、フレームワークに従い解くことができる
Stage2α: 初見の難問含め、どんな問題であっても確実に解くことができる
以降、各Stageについて、具体的な修了基準・目的・勉強法を説明します。
Stage0
修了基準:
① 定義を理解している
② 定理を使うことができる
③ 計算をある程度のスピードで行うことができる

① : 定義を正確に述べられることが修了基準です。
②,③: 教科書章末問題レベルの問題が解けることが修了基準です。
目的:
Stage0はそれ自体が京大入試に課されることはありませんが、Stage1以降の内容を理解するために必要です。① は、厳密な議論をするために必要で、②,③ はStage1以降の問題を処理する上で必要です。
推薦教材: 入門問題精講IAIIBIII
学校の授業+教科書でも十分ではありますが、独学で先取り学習を行いたい方はこちらをお勧めします。
Stage1
修了基準:
① 網羅系問題集の典型問題を全て解くことができる
② ↑で扱った手法を、体系的に把握している

①: 右のような典型問題に対し、まずは「解ける」ことが修了基準です。
②: 左のように、手法を「体系的に」理解していることが修了基準です。
目的:
Stage1は、それ自体が京大入試で出題される(特に、数学IIIは全てStage1)ため必要であり、Stage2の問題を帰着した先の問題を解くためにも必要です。
また、「試験時間内に」「確実に」思いつくためには、体系化が必要になります。②: 体系化の必要性について、上記左側のフレームワークを用いて、以下の東大京大の「典型問題」を例に説明します:

手法の体系化を行うと、下記のように、それぞれの問題を同じフォームで「確実に」解くことができます。



推薦教材: なんでもいい
青チャートや一対一対応の数学など、どの問題集でも良いですが「完璧」にすることが最も大事です。「完璧の状態の作りやすさ」すなわち「問題・解答のシンプルさ」という観点で、「IAIIB: 文系の数学」「III: 医学部攻略の数学」をお勧めします。
ただ、いずれの問題集も「体系化」はできていない上に、十分シンプルとはいえないため、agoraではオリジナル教材を用いています。また「本当にわかっているかがわからない」という問題をなくすために、理解度確認の面談およびテストを毎週行っています。
Stage1α
① 全ての典型問題に対し「答案の型」がある
② 論理的に正しい議論(思考+記述)ができる
目的:
Stage1αは、下記のために必要です:
- ①+②: 減点されない答案を書くため
- ②: 論理的に正しく考えるため
②の「論理」は、「減点されない答案を書く」ためだけでなく、Stage2以降の問題に対して考えを進める上で非常に重要です。高校数学では「論理」が非常に蔑ろにされており、市販参考書や塾・学校の教師の解答ですら(京大入試の採点官から見ると)満点とはいえないものが殆どです。ゆえに、下記の参考書で「論理」を学び、正しい答案を書く特訓をする必要があります。
【悲報】駿台、代ゼミ、北予備も同じ間違いで全滅。理系数学5番の軌跡Cを求めるとこ(結果はあってるが証明になってない)。我々数学者は変な計算テクニックや結果の暗記ではなく、ロジックの組み立て方を見てるので、そのように教えてくださいね。 https://t.co/R63dbOgChG
— 千葉逸人 (@HayatoChiba) February 27, 2019
「答案の型」を学ぶ上では、下記参考書をお勧めします:
推薦教材①: 記述式答案の書き方
「論理」を学ぶ上では、下記参考書を強くお勧めします
推薦教材②: 数学の真髄
いずれの問題集も本当に素晴らしいものであるため、agoraでも(オリジナル教材を作ることなく)こちらの教材を使用させていただいております。
ここまでを完璧にこなせば、京大文系・理系数学で2完程度に達します。
残りの3,4問は「解き方」を覚えたところで太刀打ちできない「初見の問題」で構成されるため、「解き方」中心の勉強から「考え方」中心の勉強に移行する必要があります。
初見の問題には以下2種類あり、前者をStage2、後者をStage2αで扱います。
- 標準問題: 一定の思考フレームワークに従えば解ける問題
- 難問: 一定の思考フレームワークに従っても解けない問題
Stage2
修了基準:
① 「初見の問題」に対する試行錯誤の方法を網羅的に把握している
② ↑をつねに実行でき、「未知の問題」を「解ける問題」に帰着できる

例えば、上記の問題について、それぞれ下記が修了基準です:
①: 「フレームワーク=試行錯誤の方法」が浮かぶこと

②: フレームワークを運用して「解ける問題」に帰着できること

これらを習得することで、様々な問題を、フォームを崩さずに(ゆえに、コンスタントに)に解けるようになります
目的:
Stage2は京大入試の大半を占めるため、最も重要です。
いろいろな問題の「解き方」を学ぶことで、そもそも「初見の問題を減らす」というアプローチも考えられますが、鉄緑会などの中高一貫塾に通う(十分学習時間がある)生徒を除き、殆どの高校生にとってこの勉強法による対策は時間の都合上妥当ではありません。ゆえに、未知の問題の方針を自分で立てる「考え方」を学ぶ必要があります。
また、「考え方」を学ぶ上では、「問題を大量に解き、経験と直感を磨く」勉強法も考えられますが、センスに依存することに加え「試験時間内に」「確実に」思いつくかは運次第となるため、①: 試行錯誤の方法=思考フレームワークを学ぶ必要があります。ただ、Stage2α相当の難問については、そのような学習も必要です。
思考フレームワークを学ぶ上では、下記の参考書をお勧めしますが、それぞれ注意点があります。
推薦教材① : 世界一わかりやすい京大数学
フレームワークが十分とはいえないため、フレームワークを一部再構築する必要があります。
推薦教材①': 入試数学の掌握
フレームワークは十分ではあるものの、細かすぎるゆえに使いこなすまでにかなり時間を要することに加え、例題の難易度が高く、フレームワークをそもそも身につけづらいという問題があります。
思考フレームワークを学んだ後は、それの運用練習として「過去問演習」をすることをお勧めします。逆に、フレームワークを身につけていない上での過去問演習は、「解き方」を学ぶだけの勉強になってしまい、問題が解けるか否かが「解き方を知っているか否か」に依存してしまうため、お勧めしません。
過去問演習をする際は、フォームを崩さず安定的に問題が解けるようになるため「自分の思考フレームワーク内で思考回路を説明できる」ようにすることが重要です。演習するたびに知識が増えていくような学習ではなく、演習するたびに知識が整理されるような学習を心がけましょう。
推薦教材② : 過去問(東京出版)
agoraでは、①: フレームワーク学習 ②: フレームワーク運用練習 それぞれにおいて、独自教材を用いて下記を提供しています:
①: 京大入試の約8割の問題を説明でき、かつ試験中に用いることができるようなシンプルな思考フレームワーク
②: ↑を用いる形で京大入試を解く思考回路を記述した解説
また、過去問演習においては、ディスカッションと添削を行うことで、思考回路の共有と答案作成指導も行なっています。
ここまでを完璧にこなせば、京大数学では文理問わずコンスタントに8割得点までは達します。しかし、満点を目指す(=どんな問題でも確実に解けるようになる)ためには一歩及びません。以降、「満点」を取るためのstageを紹介いたします。
Stage2α
Stage2αは「難問を確実に解けるようになる」ための段階、すなわち「東大・京大入試で満点を取る」ための段階です。この段階では、Stage2以前のような「ある程度のパターン化」から脱して、直感と論理を往復する練習を行います。
修了基準:
フレームワークが適用できない問題について、
① 今まで学んだ数学概念から,直感的に複数の方針が立てられる
② その方針に対し、論理的検証を行うことができる
③ 時間内に処理可能かを判断できる

上記のように、フレームワークに当てはまらない問題がStage2αの難問です
難問を解く上では「直感的に複数の方針を立て、それを検証していく」という流れを取ります。




推薦教材: なし
難問に対する発想を得る上では、基礎の深い理解が必須です。agoraでは、stage2αの学習と同時に、Stage0αで基礎の再構築を行います。
Stage0α
修了基準:
① 定義から定理・公式が導ける
② 各定義について「なぜそのように定義されているのか」がわかる
③ 定理・公式の数学的意味がわかる

推薦教材: 公式で深める数学IAIIBIII
目的:
① ~ ③ は、Stage2αにおける「発想の根源」になるため必要ですが、Stage1の内容を効率的に理解する上でも必要です。
例えば平面の方程式について、「 $${ \vec{a} \cdot \vec{b}}$$ が、$${\vec{a}}$$, $${\vec{b}}$$ どちらかの方向に合わせた定規で測った符号付き長さの積 」と認識していれば、「$${ax+by+cz=d}$$ なる 平面は、$${\vec{a} = (a,b,c)}$$ に対する正射影が一定の平面、すなわち$${\vec{a}}$$ を法線ベクトルとする(原点からの符号付き距離が $${\frac{d}{|\vec{a}|}}$$ の)平面である」という事実を「覚える」ことなく直観的に納得できるため、効率的な学習が可能になります。
また、① の定理・公式導出については、それ自体が問題として出題される場合があるため、対策が必要です。
最後に
「具体的にどのような計画で勉強すればよいかわからない」
「自分の勉強法が正しいか知りたい」
「フレームワークについてより詳しく知りたい」
等の質問や
「とにかく数学ができなくて困っている」
「大学進学後のイメージがつかず、学部選びに困っている」
等の相談をビデオ通話 or ボイスチャット or チャットで承っております。(学年や現在のレベルは問いません)
また、agoraの体験授業や入塾相談も承っております。入塾には人数制限がありますので、お早めに申し込みください。
agoraでは、
・京大受験に特化したオリジナル教材と映像授業
・個人の能力と忙しさ、志望校に合わせた年間・月間・週間計画立て
・毎週1~2回の進捗・理解度確認ミーティング+個別指導
・discordでの無制限質問対応+オンライン自習室
・現役京大生や社会人との進路相談会
を提供し、agora独自カリキュラムを確実にこなせ、かつ正確に理解するサポートをしております。ぜひ入塾をご検討ください。
受験生の方への短期特別プログラムも用意しています。
最後にはなりますが、受験生の皆さん、陰ながら応援しています。
京大で待っています。
