
解説 指数・対数
妻と妹から「対数を含んだ関数の微積分について教えてくれ」という依頼が別々に来た。どういうわけなのだろう。まったくの偶然である。
しかもふたりとも数学に苦手意識がある。本当にできないかどうかはともかく。
そもそも指数とか対数ってなんだ!っていうレベルなのに、そこから微分だの積分だのというのを質問してくる理由がもはやわからない。だが、頼まれた以上答えるのである。
まずは指数と対数の説明からであろう、ということで、noteに解説をするのである。
* * *
対数とはなにか?
「2の10乗は?」
「何の何乗」という考え方(つまり指数)を学んだ人ならば、この意味はわかるだろうし、掛け算ができれば計算もおそらくできるだろう。
2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
を計算すれば良い。答えは1024だ。
数学では「2の10乗」といった日本語での言い方を、短く記号で表記できるようにしているから
「2の10乗は?」
という質問は、数学のテストでは

などと出題される。2の右肩に数字を小さく書く。
生徒はこの記号を見て、ああ「2の10乗を求めればよいのだ」と頭の中で日本語に翻訳し、イコール(=)以降を自分で書き足して以下のように答えを記載することがお作法となっている。

これで正解だ。マルをもらえる。(ここまでで「指数(何の何乗)」を充分に 理解できていなければ先には進まず、指数の定義の頁に戻ること)
ここで、次の問題を考えたい。
「1024 は 2 の何乗か?」
指数を理解していれば、この問題の意味は理解できるだろう。記号で書けば
2^ ? = 1024
の “?” を求めよ、というのと同じことだ。
最初の問題は 2^10 = 1024 のイコールの後ろ(右側にあるので右辺という)、つまり 1024 を隠してしまって当てさせた。一方この
「1024 は 2 の何乗か?」
という問題は 2^10 = 1024 のうち、2の右肩の数字(指数という)を隠してし まって当てさせようということだ。
(これを日常的なことで考えるとすれば、「1分間で2倍になる細菌があった とする。この細菌 1匹が1024匹になるには何分かかるか? (答え 10分) 」 とでもいったところだ)
これについても数学では記号を用意している。次のように書く。

この log を使った数のことを、指数に対して対数(*1) と呼ぶ。logの読み方は「ログ」とか「ロガリズム」で(10グラムではない))で、だからこれは
「2を底とした1024の対数」
「ろぐにのせんにじゅうよん」
「ろがりずむにのせんにじゅうよん」
どれでも通じる。意味は「2の何乗が1024か?」あるいは「2をそれだけ乗ずると1024になる数」ということだ。試験問題ならばこうなる。

形をくわしく見てみよう。ポイントは、どの数字がどこに移動したかだ。
2^10 の ”2” は、logという記号の右下に行って小さくなってしまった。
この右下の小さい数字を「底(てい)」という。
2^10 = 1024 の ”1024” のほうが普通の大きさのままで右に書かれた。この数字を「真数(しんすう)」と言う。
生徒はこのlogの使われた問題を見て、ああ「2の何乗が1024を求めればよいのだ」とか、慣れてくると「2を底とした1024の対数を求めるんだ」と翻訳し、問題に答えられるようになる。
(*1)なんと、歴史的には指数よりも対数のほうが先に発明された(指数から覚えるほうが簡単そうだが)。ただ、対数ができた当初は「底」が決められていなかったようだ。
さっきから何度も出てきているように
2^10 = 1024
と計算してあるから、この問題では指数(右肩)の部分を答えればよい。

だ。
まとめると

となる。具体的な数字よりは文字のほうがわかりやすい人のために、下のようにも書いておこう。

慣れるまではこのまとめの式を何度も見て、記号を読んだり書いたりするとよい。(注:小さい文字はちゃんと小さく書くこと。これをていねいにやらないと、ややこしさを自分で増やしてしまう)例によって、慣れるまでは先に進んではいけないし、さらりとわかってしまった人はどんどん飛ばしてかまわない。
ここに、慣れるために例を挙げておく

ここで指数と対数について整理しておこう。
指数とは「(同じ)数字を決まった回数かける(=乗ずる)」ということであった。「何の何乗」というやつだ。
また例をあげる。

難しく考えずにこれを眺めてほしい。どんなことに気づくだろうか?
2の乗数も、さらに10の乗数だともっとはっきりするが、階段状に並んでいる。数字がどんどん大きくなると桁が増えるからだ。この「増える」という数字の大雑把な大きさの感覚はとても大事だ。指数がわかってくるというのは、数学の記号を丸暗記するということじゃない。こういうことが概念的に、もっというと肌でわかってくるということだ。
要は、「同じ数字のかけ算をつづけると、あっというまにでかくできる」ということだ。俗にバカでかい数字のことを「天文学的数字」などと呼ぶが(*2)、天文学で星だの宇宙だのを扱うときにこういった大きい数字が出てくる。
大きい数字は書きづらい。スペースを喰ってしまう。それだけが理由ではないが、とにかく今はこれをコンパクトに扱いたいと思ったとする。どうしようか。
そこで今度は対数の例をあげる。対数とは「とある数字になるためには、べつのある数字を何乗するか」ということであった。
言い忘れていたが、ある数字の対数(ロガリズム)を計算するとき、その操作を言い表す動詞は「取る」だ。(*3)
(日常的には
娘「お母さん、1024の対数取って」
母「はーい。底は2で取っていいのね?」
娘「いや、底が10のlogを取ってほしいの」
母「わかったわ。1024の常用対数(後述)を取ればいいってことね。そんなのは簡単よ。約0.301の10倍だから約3.01…」
などといった微笑ましい会話の中で見られるであろう)
(*2)べつにこれは数学用語ではない。どれくらいだったら「バカ高い」という決まりがない。決まりがないものに数学者は関心を持たない。
(*3)間違っても「ログ取って」と言われて、ログを消そうなどとはしないこと。これでは秋山仁先生のネタになってしまう。
先ほどの計算された数字の「対数を取って」並べてみる。
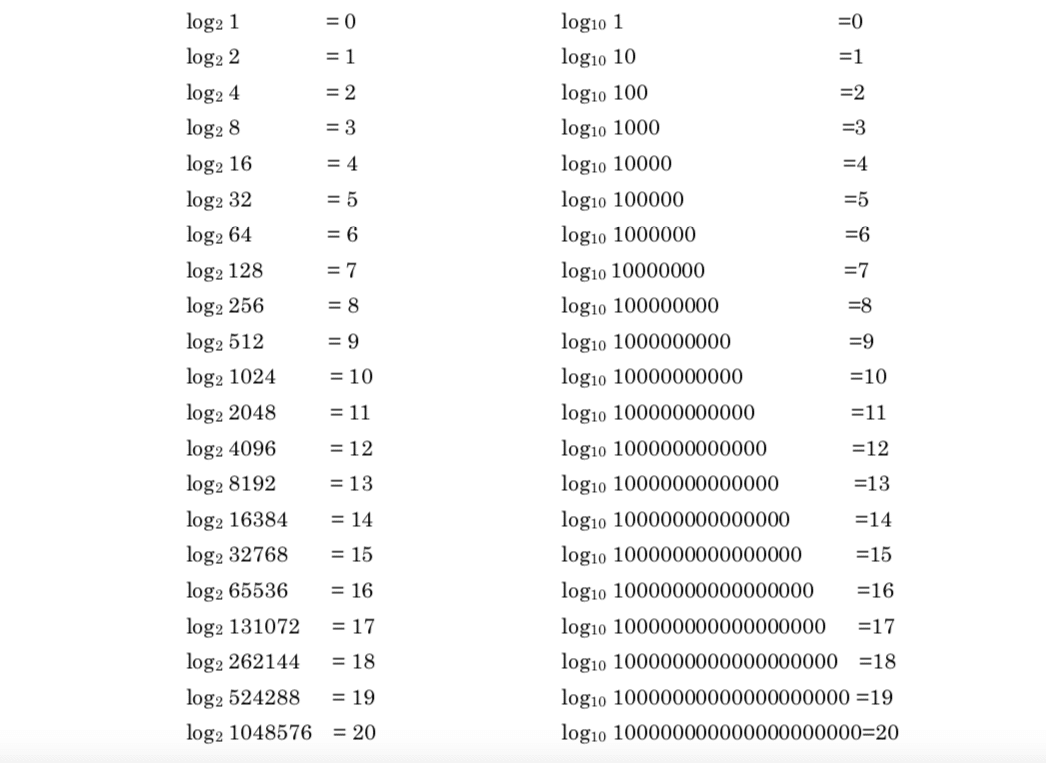
こんどはどうだろう?どんな感想を持つだろうか?
数字が1桁2桁ならば「わざわざ意味不明に違う形に変えやがって!」かもしれない。だが対数が威力を発揮するのは、数字が大きくなったときだ。とてつもなく大きな数字も、対数を取るとあっけなく小さな数字に変換されてしまう。この感覚が大事だ。
例えば底を10として対数をとれば、100万と1億は6と8の違いでしかない。6円と8円じゃあそんなに違わないかなと思ってしまうが、「この家はだいたい100万円から1億円くらいですね」と言われたら、ちょっといい加減すぎると思ってしまう。対数というのは文字通り「桁違い」の数字を、横並びにしてしまう。
だいたい100000000000000000000なんて数字、なんて読むのか知らない人のほうが多いだろう(1垓(がい)という)。10で対数を取ると、ただの20になってしまう。10で対数を取ったときに20になる数字は10^20ただ1つしかないので、これで間違いなく通じてしまうのである。
要は、「対数を取ると、でかい数字も小さく扱える」ということだ。
