
時系列データを分析してみる(4)
こんにちは、CTO室AI推進部アナリストグループの足立です。私たちアナリストグループは、主に「プロダクトの課題発見のためのデータ分析」に取り組んでいます。ユーザの皆さんがサービスをより利用しやすくなるよう、データ分析によって得られた知見は様々な場面で活用しています。
前回は、時系列データを前処理し挙動を俯瞰して見てみました。今回は前回の結果の一部を利用して、他とは異なる挙動をとる箇所を取り出してみましょう。
前回のおさらい(の一部)
データの大まかな挙動を掴む
これまで扱ってきた時系列データについて、15秒単位で移動平均と標準偏差を計算しました。そして、その結果を可視化して眺めてみると、値の変化が大きい箇所を見つけられました。
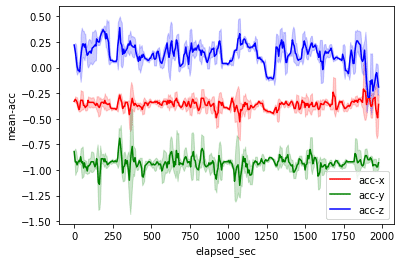
今回は上記のように、他とは異なる挙動をとる箇所を定性的にではなく、定量的に見つけてみましょう。
データから異常を検出する
異なる挙動をとるデータ点を見つけたい
時系列データにおいて、前後のデータ点の差と変化率を用いて、他とは異なる挙動をとるデータ点を見つけることができます。ここでは、移動平均によって平滑化した時系列データを利用します。

2つのデータ点の差はPythonのPandasを利用して計算し、その結果はMatplotlibを利用して可視化することにします。
import pandas as pd
import matplotlib.pyplot as plt
# 2つのデータ点の差を計算
df_dif = df_rolling_mean.diff(periods=1).fillna(0)
df_dif = df_dif.abs()
# acc-xの差を0から1の値へ変換
dif_min, dif_max = df_dif['acc-x'].min(), df_dif['acc-x'].max()
df_dif['norm_acc-x'] = (df_dif['acc-x']-dif_min)/(dif_max-dif_min)
# acc-yの差を0から1の値へ変換
dif_min, dif_max = df_dif['acc-y'].min(), df_dif['acc-y'].max()
df_dif['norm_acc-y'] = (df_dif['acc-y']-dif_min)/(dif_max-dif_min)
# acc-zの差を0から1の値へ変換
dif_min, dif_max = df_dif['acc-z'].min(), df_dif['acc-z'].max()
df_dif['norm_acc-z'] = (df_dif['acc-z']-dif_min)/(dif_max-dif_min)
# 差を可視化
plt.plot(df_dif.index, df_dif['norm_acc-x'], color='red', label='acc-x', linewidth=0.5)
plt.plot(df_dif.index, df_dif['norm_acc-y'], color='green', label='acc-y', linewidth=0.5)
plt.plot(df_dif.index, df_dif['norm_acc-z'], color='blue', label='acc-z', linewidth=0.5)
plt.xlabel('elapsed_sec')
plt.ylabel('dif-acc')
plt.legend(loc='upper right')
plt.show()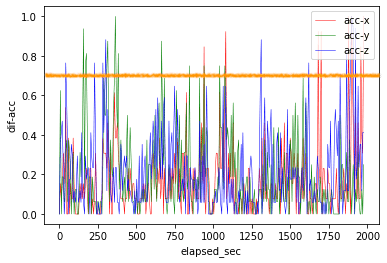
例えば、差の閾値を0.8に設定し、グラフ上へ線を引いてみます。この線を超える箇所を、他とは異なる挙動をとるデータ点(外れ値、異常値)と考えることができます。
2つのデータ点の変化率も同様に、Pandasを利用して計算しMatplotlibを利用して可視化することにします。
# 2つのデータ点の変化率を計算
df_ptc = df_rolling_mean.pct_change(periods=1).fillna(0)
df_ptc = df_ptc.abs()
# acc-xの差を0から1の値へ変換
ptc_min, ptc_max = df_ptc['acc-x'].min(), df_ptc['acc-x'].max()
df_ptc['norm_acc-x'] = (df_ptc['acc-x']-ptc_min)/(ptc_max-ptc_min)
# acc-yの差を0から1の値へ変換
ptc_min, ptc_max = df_ptc['acc-y'].min(), df_ptc['acc-y'].max()
df_ptc['norm_acc-y'] = (df_ptc['acc-y']-ptc_min)/(ptc_max-ptc_min)
# acc-zの差を0から1の値へ変換
ptc_min, ptc_max = df_ptc['acc-z'].min(), df_ptc['acc-z'].max()
df_ptc['norm_acc-z'] = (df_ptc['acc-z']-ptc_min)/(ptc_max-ptc_min)
# 変化率を可視化
plt.plot(df_ptc.index, df_ptc['norm_acc-x'], color='red', label='acc-x', linewidth=0.5)
plt.plot(df_ptc.index, df_ptc['norm_acc-y'], color='green', label='acc-y', linewidth=0.5)
plt.plot(df_ptc.index, df_ptc['norm_acc-z'], color='blue', label='acc-z', linewidth=0.5)
plt.xlabel('elapsed_sec')
plt.ylabel('ptc-acc')
plt.legend(loc='upper right')
plt.show()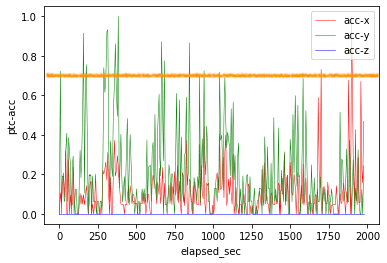
差と変化率それぞれに関するグラフを比較してみましょう。前者については、全ての変数に閾値を超えるデータ点が存在します。一方、後者については変数acc-yに閾値を超えるデータ点が多く存在します。測定方法によっては、変数の特徴を掴みやすくなることもありますね。
異なる挙動をとるデータ群を見つけたい
先ほどは、データ「点」に着目して差や変化率といった指標を計算しました。可視化した結果を眺めてみると、もう少し解像度を低くして大まかに挙動を見たいと感じるかもしれません。
そこで、ここではデータ「群」に着目してみましょう。前後のデータ群の距離を測れば、他とは異なる挙動をとるデータ群を見つけることができます。以後、データ群を部分時系列と呼びます。また、NumpyとScikit-learnのLOF(LocalOutlierFactor)を利用して部分時系列間の距離を測ります。なお、LOFに関する説明は省略します。
import numpy as np
from sklearn.neighbors import LocalOutlierFactor
## acc-xに関する処理(acc-y, acc-zも同様に処理)
part_x = []
# acc-xについて部分時系列を作成
for i in range(df_rolling_mean.shape[0]-3):
tmp_ar = np.array(df_rolling_mean['acc-x'])
part_x.append(tmp_ar.flatten()[i:i+3])
# acc-xの部分時系列から外れ値を検出
model = LocalOutlierFactor()
xflg = model.fit_predict(np.array(part_x))
xflg = np.where(xflg<0, 1, 0)
# 外れ値フラグを可視化
plt.plot(df_rolling_mean.index[:-3], xflg, color='red', label='acc-x', linewidth=0.5)
plt.xlabel('elapsed_sec')
plt.ylabel('flg-acc')
plt.legend(loc='upper right')
plt.show()

全ての変数について、フラグの値が1を持つ箇所、重なる時間があります。そのような時間帯の挙動は、共通して他とは異なる挙動をとると見なせそうです。
まとめ
本記事では、時系列データから他とは異なる挙動をとる箇所見つけるいくつかの方法を取り上げて紹介しました。次回はこの続きとして、異なる挙動をとる箇所を予測してみましょう。
