AtCoder ABC 290 D問題 解説補足
Marking
0から番号が振られたN個のマスが並んでいる。
変数 x を次のとおりに更新し、そのマス番号に印をつけていく。
x = 0
マス x に移動する
印がついていない場合は、 x = (x + D) mod N に更新する
印がついている場合は、 x = (x + 1) mod N に更新する
2を繰り返す。
K番目に印がつけられるマス番号を求めよ。
解説
定理を2つ導入する。
定理1
$${x = D \bmod N}$$ とすると
$$
\begin{align*}
x + (r-1)D & \equiv rD \pmod N \\
\end{align*}
$$
証明
$${D \bmod N = {\color{red}x}}$$ より、$${D = mN + {\color{red}x}}$$ と置くと、$${{\color{red} x} = D - mN}$$ であるから、
$$
\begin{align*}
{\color{red}x} + (r-1)D &= (D -mN) + (r-1)D \\
&= rD - mN \\
& \equiv rD \pmod N \\
\end{align*}
$$
ゆえに印がついていない場合は、
0 → D mod N → 2D mod N → 3D mod N → … → rD mod N
とマスを移動していく。
定理2
DとNの最大公約数を g とし、 $${N = ng}$$ とした時、 $${rD \bmod N}$$ の周期は n である。
証明
正整数 N, D において、最大公約数を g とすると、
$${N = ng}$$
$${D = dg}$$
となる n, d が得られる。
この時、N と d が互いに素であるから、mod演算において d で割ることができる。
$$
\begin{align*}
D &\equiv g \\
2D &\equiv 2g \\
3D &\equiv 3g \\
&\vdots \\
(n-1) D &\equiv (n-1)g \\
nD &\equiv ng = {\color{red}0}\\
(n+1)D &\equiv (n+1)g = {\color{red}g} \\
&\vdots \\
\end{align*}
$$
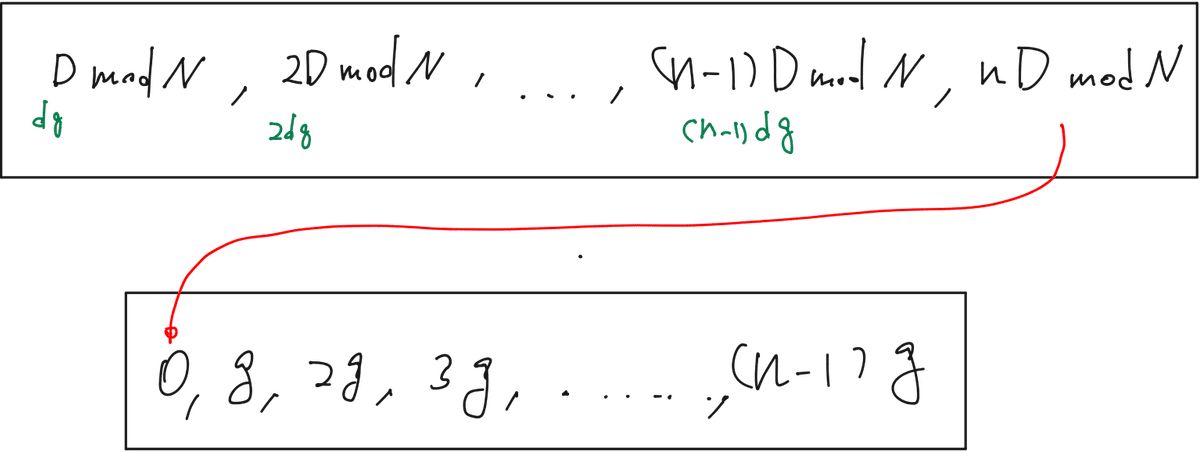
従って、 $${rD \bmod N}$$ は 周期 n である。
定理1, 2 からDとNの最大公約数を g とし、 $${N = ng}$$ とした時、
マスの移動を n 回行うと同じマスに再度訪れることとなる。
ex N = 6, D = 8のとき、 g = 2 であるから、 n = 3 となり、 3回目の移動で印があるマスに訪れることになる。

ゆえに K回移動して、マスの番号が
$$
(rD + q) \bmod N
$$
であったとすると、0からスタートし、周期 n より、
$${r = (K-1) \;\%\; n}$$
$${q = (K - 1) \;/\; n}$$
が導かれる。
解説追記
NとDの最大公約数が g とすると、これは N x D の長方形 を 正方形 g で分割できることを意味する。
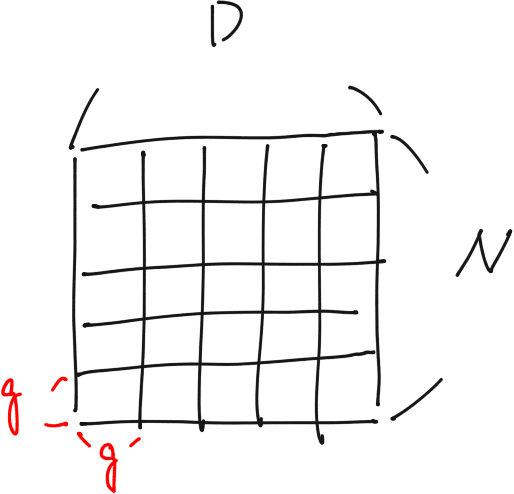
従って K番目に移動するマスの番号 $${(rD + q)\bmod N}$$ は、
以下の図のように、ブロック g を並べることで求めることができる。

