AtCoder ABC323 D問題 解説補足
問題
https://atcoder.jp/contests/abc323/tasks/abc323_d
スライムの結合
サイズの種類が N 個あるスライムにおいて、
サイズ $${S_i}$$ の スライムが $${C_i}$$ 匹いる。
同じサイズ同士のスライムが結合できる時、最小で何匹のスライムにすることができるか?
(ただし結合後は、サイズが 2 倍になる。)
解説
結合できるスライム同士タイプ分けする
スライムを全て最小サイズまで分解する
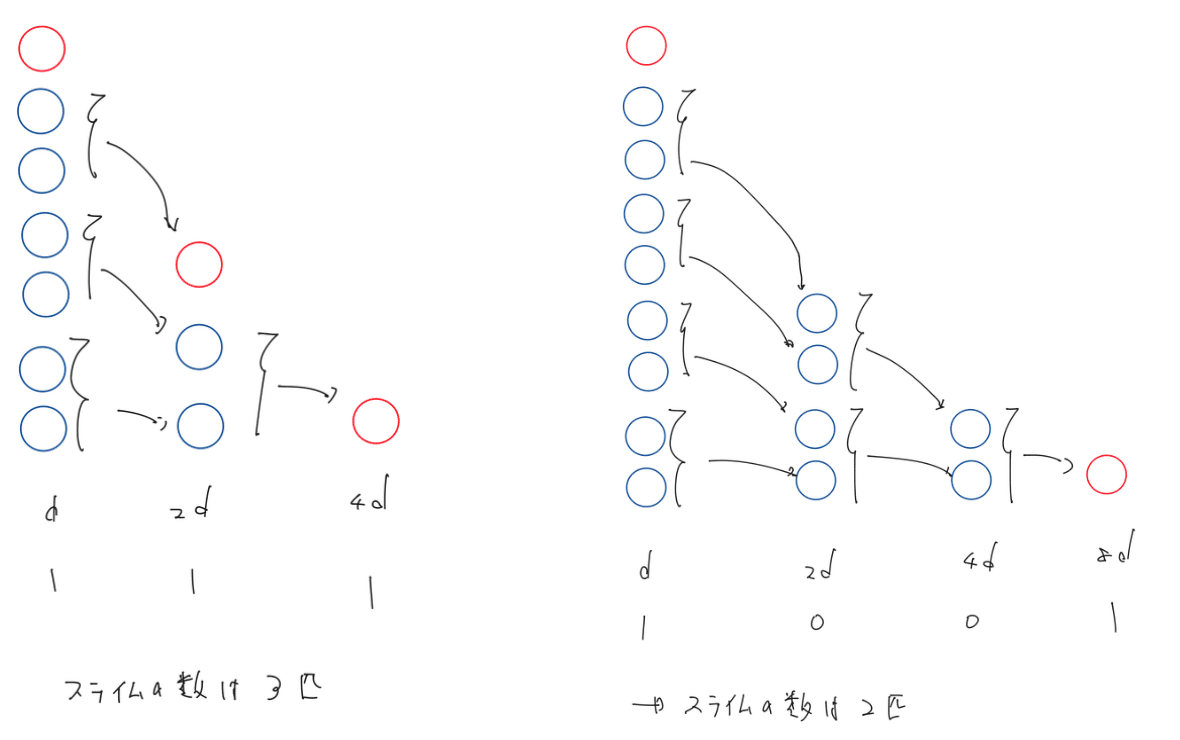
> サイズが4のスライム 1 匹は、サイズが1のスライム 4 匹が結合したスライムと考える最小サイズまで分解したスライムを再結合していく
1. 結合できるスライム同士をタイプ分けする
公式解説にもあるように、サイズ S のスライムのタイプを Sの約数である最大の奇数 として定める。

この時、タイプ d のスライムのサイズは d, 2d, 4d,…,$${2^kd}$$,.. である

2. スライムを最小サイズまで分解する
サイズ $${2^kd}$$ のスライムを一旦サイズ d のスライムに分解して、その総数を求める。
ex サイズ 4d のスライム1匹は、サイズ d のスライム4匹へと分解できる。

サイズ $${2^kd}$$ のスライムの数が $${A_k}$$匹とすると、
タイプ d に属するスライムの総数 c は、以下の等式で求まる。
$$
\text{c} = A_0 + 2A_1 + 4A_2 + 8A_3 + ...
$$
3. スライムの再結合
サイズ d 同士のスライムを結合すると、サイズ 2d に桁上りする。

上記のように考えていくと、サイズ 2d 同士のスライムを結合すると、サイズ 4d に桁上りしていくので、
結局最終的なスライムの数は、2で求めた c の値を2進数で表現して、ビットの値が1の数を数えれば良い。
// 整数cのビットの値が1である数をカウントする
while c > 0 {
if c & 1 == 1 {
//
cnt += 1;
}
c >>= 1;
}