AtCoder ABC330 B,C 最小値問題 解説補足
B - Minimize Abs 1
以下の数式において、 a と x の範囲 [l, r] が与えられる時、解が最小値となる x を求めよ。
$$
|x - a| \quad(l \le x \le r)
$$
解説
y = |x-a| とすると、グラフは以下のようになる。

従って a の位置がどこにあるかで、最小値が決まる。
(i) l <= a <= r ならば、最小値は x = a の時

(ii) a < l ならば、最小値は x = l の時
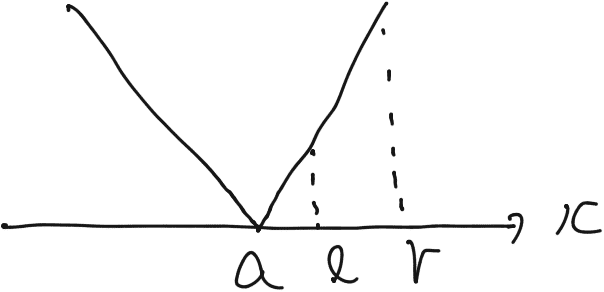
(iii) r < a ならば、最小値は x = r の時

C - Minimize Abs2
以下の数式において、Dが与えられた時、その最小値を求めよ。
$$
|x^2 + y^2 - D|
$$
制約
x, y は非負整数
1 ≤ D ≤ $${2 \times 10^{12}}$$
解説
変数xの範囲を定める。
題意「 $${|x^2 + y^2 - D|}$$ の最小値を求める」より、
xの範囲は、 $${0 \le x \le \sqrt{D}}$$ と定まる。
⇒ $${x^2 = D + \alpha}$$ とおくと、 $${|y^2 + \alpha|}$$ となり、この最小値は、 $${\alpha = 0}$$ のときである。
したがって $${x^2}$$ の範囲は、対称性から $${0 \le x^2 \le D}$$ で良い。
x が定まるので、$${c = x^2 - D}$$ とおくとことで、固定値cを定義できる。
問題は、 $${|y^2 + c|}$$ の最小値を求める 問題となる。
この時、
1. c ≥ 0 の時、$${|y^2 + c|}$$ の最小値は |c| (y = 0) が定まる。

2. c < 0 の時、
$${|y^2 + c|}$$ の最小値は、 yの値が整数で有ることを考慮して、 $${\sqrt{-c}}$$ に近い方の値が最小値となる。
最小値 = min($${ \sqrt{ \lfloor -c \rfloor}}$$, $${ \sqrt{ \lceil -c \rceil }}$$)

