【努力考察】努力系名言論争が数理的に決着

Guten Tag und ご覧いただきありがとうございます．
生き急ぎ系男子の-Utaku-です．

今回はインテリ感を出すために（笑），有名な努力系名言である

『努力は必ず報われる．もし報われない努力があるのならば，それはまだ努力と呼べない』

について数理的観点から考察します．

結果から申し上げますと，数理的に正しい名言でした．
では，Let me explain!

（※以下は，あくまで-Utaku-の個人的見解であり，発言者である王貞治様の名誉を気付ける意図は皆目ございません．
ご理解いただいたうえでご覧いただきたく存じます．
また，名言の出典を明確にできないことに関しまして，予めご了承ください．）

1. 初見の印象

いや～さすが王貞治選手ですね．
まさに努力を続けたからこそたどり着いた人生の教訓かと思います．

・努力に対して何かしらの報いがないのだったら，まだまだ努力が足りない
・結果が出るまで努力を続けなければならない

のような解釈がなされるかと思います．

某，金ぴかの英雄王も

？？？「まさに不撓不屈，人間の忍耐の究極よな．」

なんてつい言ってしまうんじゃないでしょうか？

しかし，昔塾講師をしていた頃，生徒にこの名言を教えたところ，

「成功しないと努力なんて意味がないってこと？」
「成功した人だから言えるんだよ！」

なんて返されたのを覚えています（笑）．

確かになぁと思いつつも，何と言いましょうか．
たった2文なのに，

「結果を得たかったら，結果を得られるまで努力するしかない」

という強力さをもっているんですよね(-_-;)．

正しそうだけれど，なんとなく腑に落ちない．
そんな感じでした．

しかし，数理的観点から考察すると，やはり正しい名言だったのです．

2. 命題とは

ここでは，命題の考えかたの導入を試みます．

命題とは
”論理学において判断を言語で表したもので，真または偽という性質をもつもの．”（命題 - Wikipediaを参照）
です．

真と偽は雑に言うと，それぞれ「合ってる」と「間違ってる」に相当します．

ある命題pおよびqが存在する時，
pならばqという命題は次のように記載します．

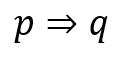
また，命題pに対して，その否定（○○じゃない　の意）は次のように記載します．

このとき，（qじゃない）ならば（pじゃない）は次のように記載ます．

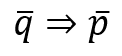
「pならばq」に対して，上の命題を対偶といいます．

なんと，元の命題とその対偶の真偽は一致するのです．
もはや全く同じ意味となります．

つまり，元の命題が真であれば，その対偶はおのずと真になります．

3. 名言に命題の考え方を導入

では，
『努力は必ず報われる．もし報われない努力があるのならば，それはまだ努力と呼べない』
に対して，命題の考え方を導入しましょう！

次のように定義します．
・命題p：任意の努力が存在する
・命題q：ある報酬が存在する

はじめに，1文目
「努力は必ず報われる」は
「任意の努力が存在するならば，ある報酬が存在する」
となりますね．（写像的に言うと全射です）

「努力すれば何かしら得られるものがある」みたいな意味になると思います．

つぎに，2文目
「もし報われない努力があるのならば，それはまだ努力と呼べない」
は何も報酬が得られていない状態から，努力の評価を行っているわけですから，
「任意の報酬が存在しないならば，ある努力が存在しない」
となりますね．

これは，「何も結果が得られなかったのなら，努力が足りないもしくは，努力を全くしていななかったのではないか」みたいな意味になると思います．

もうお気づきの方もいるかと思いますが，
1文目と2分目の命題は対偶になっています．

つまり，
「努力は必ず報われる」
と
「もし報われない努力があるのならば，それはまだ努力と呼べない」
は命題の観点から同義です．

よって，
「努力は必ず報われる」
を無意識に真としているからこそ，
「もし報われない努力があるのならば，それはまだ努力と呼べない」
もおのずと真になるのです．

同じことを2回言っているのと変わらないということですね．

4. まとめ

王貞治様の名言である，

『努力は必ず報われる．もし報われない努力があるのならば，それはまだ努力と呼べない』

における1文目と2文目は数理的に同じ命題であり，
論理構造の観点から正しいと言えます．

だからと言ってどうということはありません．

皆さんご自分が信じる道を歩まれてください．m(__)m

ではでは，Auf Wiedersehen!