【努力考察】限界とは何かについて考えてみた

こんにちは！

プレワ飲んで筋トレしたら三頭筋の筋肉痛がなかなかとれない-Utaku-です
(^o^)

今日お手洗いに行く途中，
就職活動で『限界』について質問されたことを急に思い出しました
（なぜだ笑）

自分なりの答えを言語化するのが非常に難しかったのを覚えています．

なぜなら・・・

数学的に理解していたからです！！

急に何を言い出すんだUtaku！？
一体noteはどうなるのか！！！

次回『限界とはなにかについて考えてみた』

来週も観てくれよな！！！

はい．すみませんはしゃぎすぎました．

というわけで

数学×努力シリーズ第4弾です！

前回はこちら↓

１．あなたにとって『限界』とは？

これがですね

私が就職活動していた時に面接で聞かれた質問です
(-_-;)

おそらく大学生活で部活に明け暮れていた方や何かに挑戦していた方は，

志望動機やアピールポイントに

『私はつねに限界に挑戦できる人間です』

とか書くのではないでしょうか？

でも限界って難しいですよね

例えばダンベルベンチプレスで40 kg × 10 レップが限界だと思っていても

11 レップ目で10 cmでも挙上出来たら ”10 レップ目きっかしで限界”

とは言えませんよね．

ですから私は表題の質問に対して，

真の限界とは，努力してかつての自分を超えていく中で限りなく近づいていく対象

と答えていました．

でもこれは言語化するのであればこうなるという回答であって，
ちゃんとねちねち説明するためには数式が必須だったんですよね

(´・ω・｀)

２．筋トレを例に定式化

筋トレでよく言われていることをベースに，
限界について定式化していきましょう．

筋トレってなんとなくこんなこと言われてますよね

・ナチュラルには限界がある
・初心者の内は筋肉がいっぱいつく
・年数を重ねると一年につく筋肉量は減っていく

よって次のように定義します．

全て説明していきます．

努力変数tは，何かしらの努力を表しています．
勉強しかり，筋トレしかり
結果を得るために費やす何かですね．

結果獲得速度vは，その結果が得られる速度を表しています．
筋トレであったら，”一年で○○ kg筋肉がつく”みたいなものに相当します．

結果獲得速度係数kは，その補正係数です．

結果xは努力によって得られた何かしらの結果ですね．
筋トレであったら，”BIG3が○○ kgになった”ことや”骨格筋量が○○ kgになった”みたいなものが相当します．

真の限界R_Lは，生物学レベルでどうしても超えようがない限界です．
”ナチュラルボディビルダーの骨格筋量の限界”とかがこれに相当します．
（この限界を破るのが多分アナボリックステロイドですよね(-_-;)　）

仮の限界R_0はR_Lへの途中で至る，ある結果の値です．

さて，これらの値の関係は次のようになると考えています．

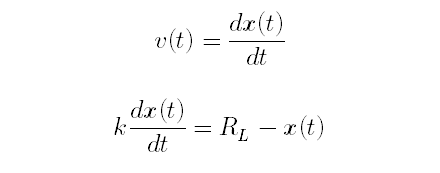
上式は言わずもがな速度と変位のアナロジです．

結果獲得速度vは結果xの微分となっています．

続いて下式です．これが前述の”筋トレについてよく言われていること”をうまく表していると思います．ちなみに一変数微分方程式としています．

イ）ナチュラルには限界がある

これは微分方程式が真の限界R_Lを含んでいることから考慮できています．

ロ）初心者の内は筋肉がいっぱいつく

これは右辺と左辺を比較していただければよく分かります．

初心者の内は，筋トレを初めて間がなく，結果xが小さい時期であると考えられます．

このとき，図1のように右辺である真の限界R_Lとの隔たりR_L - xは大きいです．
（ナチュラルのボディビルダーと初心者の骨格筋量を比べたらその差は大きいですよね）

すると左辺である結果獲得速度vも大きくなることが分かります．

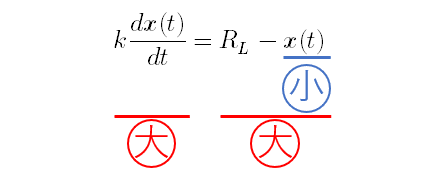
図1　右辺と左辺の大小関係

ハ）年数を重ねると一年につく筋肉量は減っていく

これもロ）と同様に考えることができます．
年数を重ねていくと結果xは大きくなっていくと思います．

このとき，図2のように右辺である真の限界R_Lとの隔たりR_L - xは小さくなっていきます．

すると，左辺である結果獲得速度vも小さくなっていきます．

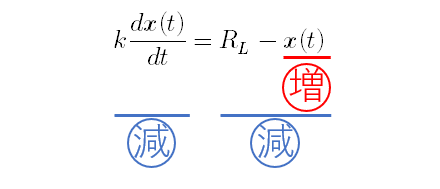
図2　左辺と右辺の増減関係

いかがでしょうか？

立式については筋トレを例にとったときに実際に即しているのではないでしょうか？

３．解こう(*👁ω👁*)

いい感じの微分方程式に仕上がったので，変数分離法で解いていきます．

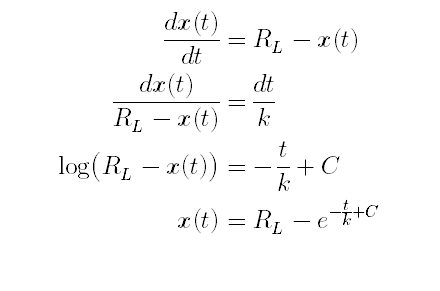
まだ未知積分定数Cを含んだ形になっています．
とりあえず，結果xの初期値を0にして解きます．

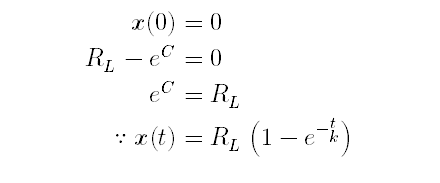
わーいわーい解けました～(/・ω・)/

せっかく解けたので以下のようにしてプロットしてみます．

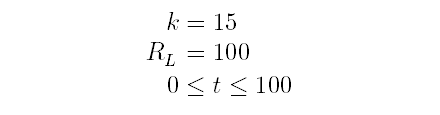
具体的なグラフは図3のようになります．

図3　努力と結果の関係

４．グラフの解釈

図3は手前味噌ですが，なかなか真理をついた結果になっているかと思います．

前述のように筋トレは以下のように言われていますよね．

・ナチュラルには限界がある
・初心者の内は筋肉がいっぱいつく
・年数を重ねると一年につく筋肉量は減っていく

イ）ナチュラルには限界がある

初めに，1点目ですがこちらは図4のようなxがR_Lに近づきつつあるエリアを表しています．

数学では漸近線といいます．意味はその値に限りなく近づくけれどもその値自体にはならないみたいな感じです．

図中では重なっているように見えます．

ですが，t=100のときでさえも，結果xと真の限界R_Lの値はそれぞれ99.8827と100であり，結果x自体は100ではありません．あくまで，100に限りなく近くなっているだけです．

これはt=∞としても同じように100に近づくだけで，100自体にはなりません．

つまるところ，生物学的限界はその限界自体には達することはできず，限りなく近づくことしかできないみたいな解釈になります．

図4　ナチュラルの限界

ロ，ハ）初心者と中級者はつく筋肉量が異なる

次に，2点目と3点目ですが，図5のように整理されます．

やり始めてしばらくは費やした努力tに対して，ついてくる結果xは大きいです（図5 (a)）．対して，年数がたつに従って，同じ努力の量であってもついてくる結果の伸びは小さくなります．（図5 (b)）

　　　　　　　　　(a) 初心者の場合

　　　　　　　　　(b)中級者の場合

図5　努力と結果の伸びの関係

いい感じに説明がついたかと思います．

では初めに戻って私にとっての限界は

真の限界とは，努力してかつての自分を超えていく中で限りなく近づいていく対象

でした．

それでは日々超えていくべきかつて自分が限界と思っていたものはグラフ上ではどのように表せるでしょうか？

ここで初めに定義した仮の限界R_0が登場します．

真の限界R_Lと仮の限界R_0の関係は図6のようになります．

図6  仮の限界のその先

仮の限界はスタート地点と真の限界との間に常に位置します．

我々が思う限界はおそらく自分が想像しうる範囲にどうしても収まってしまいます．

よって自分が思っている限界は仮の限界R_0に相当します．

そして永遠にたどり着けない真の限界の間には無限に仮の限界が存在します．

そして，仮の限界のその先は常に存在しており，それが真の限界になることは絶対にありません．

前述の通り，真の限界には限りなく近づくことしかできないからですね．

５．まとめ

今回は

・筋トレをベースに，限界に関する方程式を立てて

・それについて変数分離法を用いて解き，

・グラフにプロットして

妥当な結果が得られました．

私は自分が思っている限界（≒仮の限界）を超えたときは，常にこれが通過点にしか過ぎないと考えています．

というのも真の限界に達することが決してなく，

結果が得られる速度が小さくなっていく中で少しずつ近づかざるを得ないからです．

グラフからそれは明確ですね．

ですから，もし”あなたにとって『限界』とは”と聞かれ，どんな答え方でもいいのなら私はこう答えるでしょう．

微分方程式kdx/dt = R_L - xの漸近線のようなもの