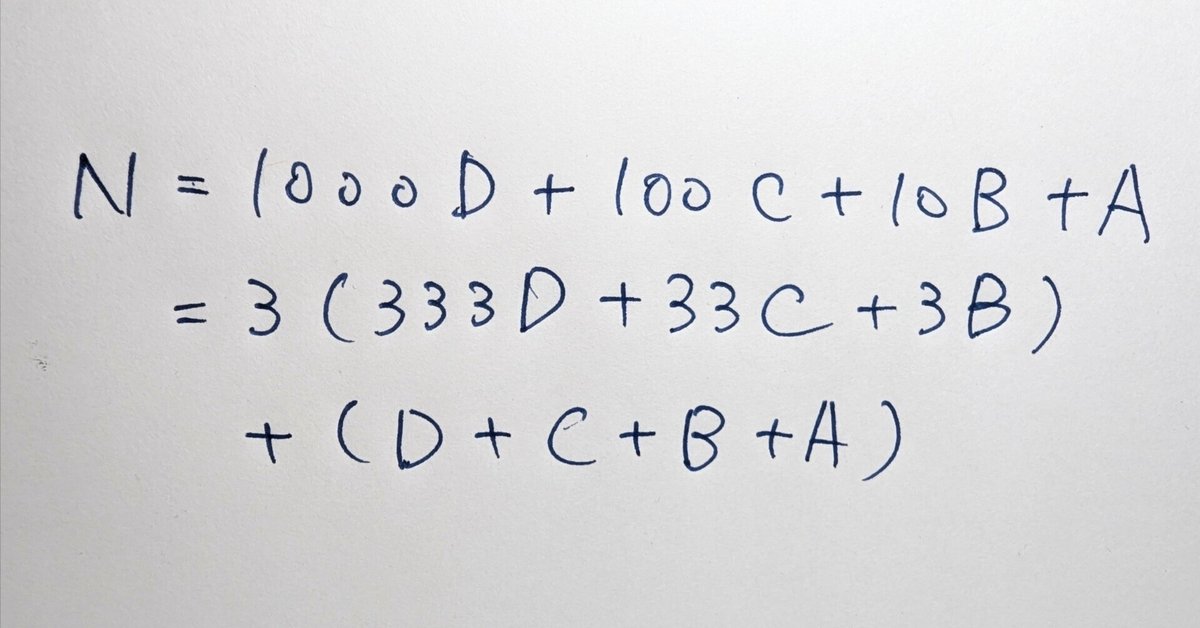
倍数判別法 2, 3, 4, 5, 6 編

以前書いた計算ミスしづらくする方法のなかで倍数判別法に触れました。
今回はこれについて思い出を交えて書いてみます。

僕が習ったのは、中学受験のために通っていた塾ででした。この倍数判定法は中学受験では必須の知識になっています。

この時もただ知識として教わっただけで、その判定法の証明までは教わりませんでした。小学生で証明まで理解するのはちょっと難しいんですよね。

中学に入って、数学の授業中にふとこの判定法の証明を今なら自力でできるのではないかと思ってやってみました。その時の証明を再現してみたいと思います。

証明を始める前に下準備。
４桁の自然数N。DCBAを考えます。

$${N=1000 \times D + 100 \times C + 10 \times B + A}$$

たとえば3960だったら。$${D = 3, C=9, B=6, D=0}$$となります。
4桁までしか考えなくて良いのかと思われるかもしれませんが、以降の説明を読めば4桁まで考えておけば桁数に関係なく成り立つことはわかると思います。

2の倍数の判別法

これは簡単。偶数だったら2の倍数ですね。
各桁を２で割ってみます。

$${N=2 \times 500 \times D + 2 \times 50 \times C + 2\times 5 \times B + A }$$

割り切れる部分を集めると、10の位以上は必ず割り切れることがわかります。

$${N= 2 \times( 500 \times D + 50 \times C + 5 \times B) + A}$$

したがって1の位が2で割ることができれば2の倍数です。

このように各桁ごとに割っていって明らかに割り切れる部分とそうでない部分に分離することで判別法を導き出すことができます。

3の倍数の判別法

これが今回のハイライト。これを知れば以降は読まなくても自分で判別法を作り出せます。

各桁を3で割ってみます。

$${N=(3 \times 333 + 1) \times D + (3 \times 33 +1) \times C + (3 \times3 +1) \times B + A}$$

割り切れることが明らかな部分とそうでない部分に分けてみると以下の通り。

$${{N= 3 \times ( 333 \times D+ 33 \times C + 3 \times B) + (D + C + B + A)}}$$

つまり$${D + C + B+ A}$$の合計が3で割り切れればNは3で割り切れることになります。言い方を変えると各位の数字の合計が3で割り切れればその数は3で割り切れます。

このように、割り切れることが明らかな部分とそうでない部分に分割するとき、各位の数字の係数が小さくなるように分割するのが重要です。係数が小さいほど判別法として使い勝手が良いです。

初めてこの3の倍数の判別法を知った時はとても神秘的に感じました。こんな簡単に3で割れるかどうかわかるのかと。証明を自分で編み出したときもこのようにきれいに判別法が表れて感動しました。

ちなみに9の判別法は3と全く同じになります。面白いですね。9については次回やります。

4の倍数の判別法

これも同様に各桁を4で割ります。

$${N=4 \times 250 \times D + 4 \times 25 \times C + 10 \times B + A }$$

割り切れる部分を集めます。

$${N= 4 \times( 250 \times D + 25 \times C ) + (10 \times B + A)}$$

$${10\times B+A}$$が4で割り切れればNが割り切れることがわかりました。言い換えると下2桁が4で割り切れればその数は4で割り切れます。

5の倍数の判別法

これは簡単。1の位が0か5であれば5で割れます。
各位を5で割ります。

$${N=5 \times 200 \times D + 5 \times 20 \times C + 5 \times2 \times B + A }$$

割り切れる部分を集めます。

$${N= 5 \times( 200 \times D + 20 \times C + 2 \times B ) + A}$$

1の位が5で割り切れればNは5で割り切れることが確認できました。

6の倍数の判別法

これは今までとちょっと毛色がちがいます。$${6=2\times3}$$として2の倍数かつ3の倍数と考えます。

というわけで６の倍数の判別は、偶数かどうか確認して偶数なら、3の倍数判別法を使います。

この考え方は応用できて、例えば12の倍数の判別法は$${12=3\times4}$$として、3の判別法と4の判別法を使えば良いことになります。

ひとまずここまで。次は8, 9, 11。