第13回　情報源符号化　その2（瞬時符号）

阿坂先生
今回は情報源符号化の符号語の作り方を見ていくのじゃが、まず符号語の分類を勉強していこう。

桂香助教
この分類を分かるとどんな符号が良い符号なのか理解できるようになるわ。符号の作り方までちょっと説明が続くけど我慢してね。判りやすく説明していくから。まずは、符号語の分類を勉強していくね。

麦わら君
ところで符号ってなんでしょうか？

阿坂先生
符号とは、ある記号列Xを別の記号列Yに対応づける関数fのことじゃ。

Y＝f(X)

XからYに変換することを符号化という。Yは符号語じゃ。逆にYからXに戻すことを復号という。

桂香助教
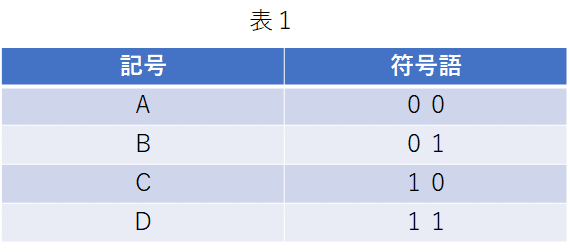
前回の例ではXがABCDの記号で、Yが00,01,10,11の符号語に当たる。

阿坂先生
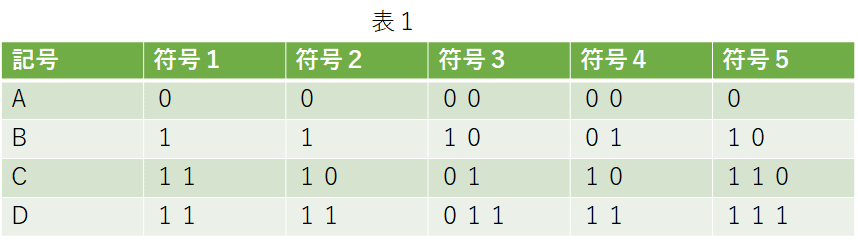
以下に符号の例をいくつか挙げてみるぞぃ。この符号の性質を見てみよう。

桂香助教
まず、特異符号を説明するわ。符号１ではCとDが同じ符号語が割り当てられているわよね。符号語の受け手が１１と受信すると元の記号がCかDかは区別できない。このような符号を特異符号というわ。他の符号２～５はすべて記号と符号語が１対１の関係で対応しているので特異符号ではないわ。このような符号は正則というわ。

麦わら君
特異符号には利用価値があるのですか？

阿坂先生
よい質問じゃ。特異符号で一旦符号化してしまうと元に戻すことができなくなってしまう。しかし、特異符号を使うことで情報は完全には復元できなるのじゃが、符号語長を大幅に短くできる。

麦わら君
若干の情報がなくなっちゃうけど、その分、符号語長を短くできるということかぁ。それはそれで使い道がありそうですね。

桂香助教
つぎに可変長符号と固定長符号を説明するわ。だいたい予想がつくとは思うけど符号語の長さがそれぞれ違うか、全部同じかの違いよ。可変長符号は表２では「符号１」，「符号２」，「符号３」、「符号５」。固定長符号は「符号４」よ。

麦わら君
こちらも難しくないですね。

阿坂先生
可変長符号についてはちょっと複雑じゃな。可変長符号は何ビット目が符号語の切れ目かぱっと見では分からない。復号する場合は固定長符号のように符号長毎に区切ることができないからのぉ。可変長符号は切れ目がどこかを判断してやる必要があるからのぅ。

じゃが、可変長符号を利用するとトータルのビット数を少なくできる可能性がある。これを今から勉強していくのじゃ。

桂香助教
可変長符号は切れ目が大事だわね。例えば「符号2」において101

という符号語を受信したら「BAB」と「CB」という2通りの解釈がある。このように複数の解釈があるのを一意復号不能というわ。これはダメな例ね。逆に1通りしか復号できない、つまりブレなく復号できることを一意復号可能というわ。

麦わら君
符号３も一意符号不能じゃないですか？010110・・・と続いたら「CCB・・・」と「CD・・・」という２つの解釈ができます。

阿坂先生
よいところに目をつけたな。実は符号３は一意復号可能なんじゃ。この符号は途中で切れているが、逆から復号していくと一通りの解釈しかできない符号なのじゃ。

桂香助教
どうしてかって？実はこの例では010110・・・ってなっていたけど、　”・・・”の部分が分かれば一通りにしか解釈できない。例えば0101101だったら「BDC」になる。

麦わら君
えー！。これは符号が3記号と短いからじゃないですか?0101101・・・101011って長くなると何通りでも解釈できそうな気がします。

阿坂先生
どんなに長くなっても符号３は一通りじゃ。実はこれまでは符号の先頭から復号してきたが、最後から復号していくと1通りであることがわかる。符号の最後から順に追っていって「００」ならA,「01」ならB,「01」ならC,「１１」ならDじゃがオマケに０が付いていると解釈したらどうじゃ？

麦わら君
なるほど。そうゆうふうに解釈すれば確かに1通りですね。

桂香助教
ただし、この符号は一意符号可能ではあるけれど、符号の全部を受け取ってからじゃないと復号できないので、あまり良い符号とは言えないわ。

なぜかというと、例えばこの符号が電話用に利用される符号とすると、話し手が話し終わるまでは、復号できないので聞き手は何も聞けない時間が長く続くということになってしまう。これでは、電話で話したときの遅延が大きくなって非常に使い勝手の悪い電話になってしまう。

麦わら君
先頭から符号語を解釈できれば、符号語を受け取り次第、音声に変換することができるので遅延は少なくできるということか。文章で言えば読点の「。」が来るまで何も情報が得られないのは不便ですもんね。

阿坂先生
そう。それで先頭から符号を復号できる符号を瞬時符号というんじゃ。

桂香助教
瞬時符号を理解するには語頭という概念を勉強しておく必要がある。語頭とはある符号の先頭から0ビット、1ビット、2ビット・・・と抜き出したものを言うのよ。たとえば、符号が１１０１ならば頭語は、（特殊な例として空のものを除けば）
１
１１
１１０
１１０１
となるわ。このすべての符号の頭語が自分以外の符号語でなければ瞬時符号と言えるのよ。つまり先頭から復号ができるということ。これを頭語条件を満たすというわ。

阿坂先生
例えば、符号３はDの０１１の語頭は０、０１、０１１になるぞい。ここで、この2番目の頭語０１は記号Cの符号語になっている。つまり、この場合は瞬時符号ではない。語頭条件を満たさない。このような符号は非瞬時符号と呼ばれる。つまり先頭から復号できない符号ということになる。

桂香助教
気をつけて欲しいのは非瞬時符号だからといって、一意符号不能と言うわけじゃない。符号３のように後ろから復号するとうまく復号できる一意符号可能な非瞬時符号もある。

麦わら君
なるほど。ところで、符号語４と５は頭語条件を満たしているね。先頭から符号できるから瞬時符号ですね。瞬時符号だと一意符号可能なんですか？

阿坂先生
そうじゃ。瞬時符号であれば必ず一意符号可能じゃ。それではまとめじゃ。表1の符号を「特異or正則」、「一意復号可能or一意復号不能」、「非瞬時符号or瞬時符号」を分けるとどうなる？

麦わら君
えーと。こんな感じですか？

桂香助教
正解よ。次回は符号の木を勉強していくわ。