
第20回 誤り訂正符号の基礎
阿坂先生
今回から誤り訂正符号を勉強していこう。シャノン理論が確率・統計を基礎としていたのに対し、誤り訂正符号の基礎の符号理論は代数学が基盤となっていて、異なった理論体系を持っているのじゃ。
桂香助教
まずは誤り検出から勉強していくわ。その後に誤り訂正について解説するわ。
麦わら君
誤り検出と誤り訂正はどう違うのですか?
阿坂先生
誤り検出は送信した信号に誤りが発生しているかどうかが分かることじゃ。誤りの訂正はできない。誤り訂正は誤りを検出して正しい情報に修正することをいうのじゃ。
麦わら君
誤り検出は誤りがあることがわかっても修正はできないんですね。
(1)誤り検出
阿坂先生
誤り検出の具体的に例を挙げて説明して行こう。たとえば、送信信号が2ビットだとして、00,01,10,11の4つだとする。これを情報ビットということにするぞぃ。
桂香助教
ここで誤りがあるかどうか調べるビットとして検査ビットを用意するわ。誤り検出にはパリティチェックというものがよく使われているの。パリティチェックの検査ビットは、情報ビットと検査ビットの1の総和が偶数になるよう設定されるの。総和が偶数になるように検査ビットを1か0のどちらかに決めるのよ。具体的には以下よ。

阿坂先生
情報ビット+検査ビットを合わせたものを符号語とするのじゃ。そして、もし、011を送ったときに受信側で先頭の1ビットに誤りが発生し111を受信したとき受信した側はどう思うじゃろ?
麦わら君
そうですね・・・。情報ビットと検査ビットの1の部分の和が偶数なのに奇数になるのはおかしい。どこかで誤りが発生したという判断をするのですか?
桂香助教
そのとおりよ。このとき、1ビット誤ったとして誤りの訂正はできるかしら?
麦わら君
111を1ビット変化させると符号語である011,101,110の3パターンがあり、どれが送信されたかは断定できないですね。
阿坂先生
だから、誤り検出なのじゃ。誤りの訂正はできない。
麦わら君
わかりました。あと気になるのは、101の場合で2ビット間違えて011になると3番目(101)が2番目(011)の符号になるから間違いを検出できないじゃないですか?というか受信側が間違っているのに正しいと判定してしまう。
阿坂先生
それもそのとおりじゃ。パリティビットは1ビットまでの誤りしか検出できない。2ビット間違えると検出ができないのじゃ。だが、誤り率があまり大きくない場合、2ビット誤る確率は1ビットだけ誤る確率よりもぐっと小さいことは分かるんじゃろ?
桂香助教
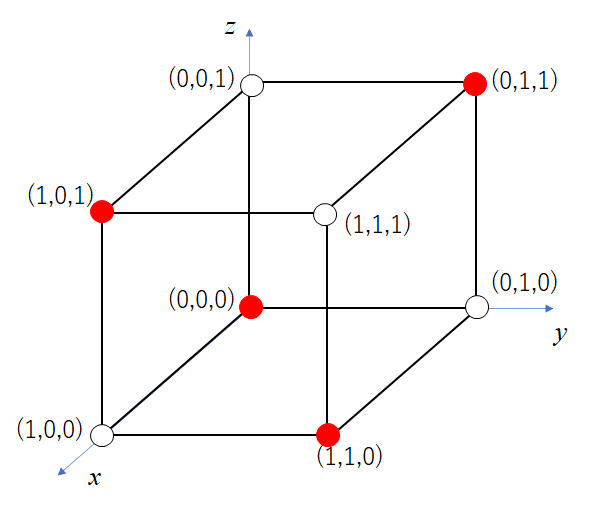
3ビットの符号語(赤点)を(x,y,z)の3次元で描いてみると以下のようになるわ。
麦わら君
図で表すと符号の構成がよく分かりますね。赤点の符号語が1ビット間違えると白点に移動する。白点になってしまうと誤りが発生したってわかる訳ですね。どの赤点でも1ビットずれると白点になりますね。
桂香助教
それに2ビット誤ると辺を2つ移動することになるから別な符号語になってしまう。こうなると誤りの検出ができなくなることを意味しているわ。
阿坂先生
今調べたパリティ符号は、1ビットの誤り検出が可能だから単一誤り検出符号というぞぃ。
麦わら君
あーなるほど!!誤り訂正の符号の仕組みが分かってきました。前回の講義で2の1000乗のパターンのうち、2の531乗のパターンを選ぶってあったじゃないですか?今回もことも同じことですね。2の3乗の8パターンから2の2乗の4パターンを選んでいるということですね。こうやって、全パターンから実際に送るパターンを減らすことで誤り検出や訂正ができるようになることか。
桂香助教
そのとおりよ。全パターンを使い切らずに余裕を残しておくことで誤りの検出や誤り訂正ができるようになるってわけ。
麦わら君
ふむふむ、理解が深まってきました。では、誤りを修正したいとなると余裕を増やせばよいことになるのかな?
(2)誤り訂正
阿坂先生
そのとおりじゃ。では、誤り訂正できる例を見てみよう。余裕を増やした例として、1を送るとき111,0を送るとき000とした3連送符号を考えてみるぞぃ。
桂香助教
この符号は前に勉強したとおり、多数決ルールを使えば1ビット間違った場合でも誤り訂正可能よ。たとえば、110を受信した場合は1のほうが多いから送信したものは1だと分かる。
麦わら君
誤り検出のパリティ符号では余裕が8個中4個だったのが、今回は8個中6個の余裕になったから誤りも訂正できるようになったんですね。
桂香助教
さきほどと同じように(x,y,z)で絵を描いてみよう。

麦わら君
000と111は対角線の位置。2つの距離が一番離れているから修正可能なのかな。
阿坂先生
そう!この離れているっていうのが大事な感覚じゃ。ここで、誤り検出や誤り訂正の概念をさらに明確にするために符号語どうしの食い違いを測る距離を導入しよう。ふたつの符号語があったときに0と1が食い違っている数をハミング距離ということにするぞぃ。
桂香助教
たとえば、下の2つの符号語のハミング距離は3よ。

ハミング距離を式で描けば以下よ。
ハミング距離 = ∑(符号語1+符号語2)= ∑(符号語1ー符号語2)
この符号語は0と1しかない演算で、GF(2)といったりもするけれど、-1は1になるのよ。だから上記の式で足し算と引き算は同じ計算になる。他は排他的論理和になるのは説明したわよね。1+1=0、1+0=1、0+1=1、0+0=0よ。
阿坂先生
このハミング距離は距離の3公理を満足するぞぃ。
桂香助教
距離の3公理とはなんであったかというと・・・・
(1)d(p,q) ≥ 0である、等号成立はp=qのとき(非負性)
(2)d(p,q) = d(q,p) (対称性)
(3)d(p,q) + d(q,r) ≥ d(p,r) (三角不等式、三角性)
pとqがベクトルと考えて、d(p,q)を長さ|p-q|だと考えれば良いわね。

距離をイメージすれば(1)~(3)は満足できることが分かるんじゃないかしら。
阿坂先生
このハミング距離が符号の性能の指標になるんじゃが、符号語がたくさんあるとすべての組み合わせでハミング距離を計算する必要がある。これはちょっと計算がめんどうじゃな。この計算が簡単にできる方法は次の線形符号で勉強するぞぃ。
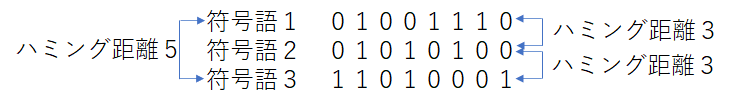
桂香助教
そして、すべてハミング距離が最も小さいものを最小距離と呼ぶこととする。たとえば、上記の符号の最小距離は3じゃ。
阿坂先生
最小距離はこの符号が使われたときの最悪の性能を示すことになるぞぃ。良いところを参考にするよりも悪いところに注目したほうがシステムは安全に設計できるな。
麦わら君
最小距離が小さいと誤り訂正が難しいことはわかるのですが、最小距離がいくらだとこのくらいの誤り訂正能力があるとかわからないのですか?数値で知りたいです。
阿坂先生
最小距離dminが分かるとdmin-1個までの誤り検出が可能であり、
⎿(dmin-1)/2⏌までの誤り訂正が可能なんじゃ。⎿ ⏌は床関数じゃ。前に天井関数を勉強したが床関数はその逆の切り捨ての関数じゃ。⎿1.45 ⏌=1じゃ。
桂香助教
最初に勉強したパリティビットの場合は誤り検出可能の符号だったわ。ハミング距離はどれも2だわ。だから最小距離dminも2。だからdmin - 1=1なので1ビットの誤り検出が可能よ。
阿坂先生
絵を描くと以下じゃ。dmin個まで間違ってしまうと他の符号語になってしまうがそれより1個少ないdmin-1個までなら誤り検出可能だということになるな。

麦わら君
あれ?この場合だとdmin+1の場合も誤り検出可能ですよね。
阿坂先生
そうじゃな。誤り検出できないのはdmin個だけ間違った場合じゃ。ただ、誤り率が大きくない場合、dmin-1個だけ間違うのとdmin+1個間違うのはdmin-1個間違うほうが確率が高いじゃろ。ここでは、dmin個までの誤りを想定しておるぞぃ。
桂香助教
誤り訂正の場合は⎿ (d-1)/2⏌個までの誤り訂正が可能よ。これを絵にかく以下になる。

麦わら君
なるほど、どっちの符号語に距離が近いかで符号語を判定するってやつですね。でも具体的に⎿ (dmin-1)/2⏌個以下の誤りはどうやって訂正するのですか?
阿坂先生
一番簡単なのは、それぞれの符号語に対して⎿ (dmin-1)/2⏌個以下の誤りパターンを用意しておけば良いぞい。受信信号が用意したパターンのどれになっているか調べれば良いだけじゃ。
桂香助教
上記の誤り訂正が可能な000と111の例では⎿ (dmin-1)/2⏌は1になるわ。dmin=3だからね。だから1ビットまでの誤り訂正が可能。誤りパターンは
000の1ビットの誤りパターンは001、100、010
111の1ビットの誤りパターンは011、101、110
上記の誤りパターン以外に符号語のそのものの2つを加えると2の3乗の8パターンになりすべてのパターンが網羅されている。受信した信号がどれに属しているか調べれば送信符号語を決定できることになるわ。
阿坂先生
上記の例では1個の誤りパターンじゃった。一般にr個までの誤りのパターンを想像できるかのぉ?前回にコンビネーションCで誤りパターン数を計算したな。。そして、ある符号語の誤りパターンの集合をハミング球というのじゃ。ちょうど符号語を中心に半径rだけ離れた点が球のイメージじゃ。

桂香助教
このハミング球が重ならなければ、r個の誤り訂正ができるわけよ。重なっちゃうと誤った信号がどちらの符号語の誤りパターンに属しているか分からなくなるから、重ならないようにrを設定する必要があるわ。
阿坂先生
最小距離がdminの場合はハミング球が重ならないようにハミング球の半径rは⎿ (dmin-1)/2⏌以下に設定する必要があるってことじゃ。そしてrをそのように設定すれば、受信した信号がどの符号語の勢力圏にあるか調べることで誤り訂正できるわけじゃ。

麦わら君
ハミング球がそれぞれ離れていれば、受信信号が特定の符号語のそれぞれの勢力圏に入るわけだから修正可能ってわけですね。ただ、ハミング球が全パターンを覆いつくすようにしておかないと、どのハミング球にも属さない受信信号があるとどう修正していいか分からなくなりますからね。
桂香助教
そうね。ハミング球が全パターンを埋め尽くす符号化が求められるわ。これについては次回勉強するわ。
麦わら君
もう1つ言えるのは、勢力圏を超えほどの多数のビットが間違ってしまうようなら誤り訂正に失敗するということですね。あるハミング球を飛び出して別なハミング球に入ってしまうってことです。
阿坂先生
そのとおりじゃ。rを超えた数の誤りが発生してしまうとなりの勢力圏にいってしまうから、間違って修正されてしまうな。できるだけrは大きくする必要があるがrを大きくすると符号語の数(ハミング球の数)が減ってしまうため、伝送できる情報量が減ってしまうことになるのじゃよ。
桂香助教
これは前回の通信路符号化定理の講義で話したわよね。
麦わら君
もう一度、勉強してみます。
いいなと思ったら応援しよう!

