第15回 情報源符号化 その4(符号化の方法)
阿坂先生
今回はできるだけ平均符号語長を短くする符号化の方法を考えていくぞぃ。平均符号語長Lは、各符号語長をl(i)として、その符号語の発生確率をp(i)としたとき以下のように計算できる。αは符号語の総数じゃ。

桂香助教
これから作る符号語は語頭条件を満たす、つまり、瞬時符号であって欲しいので、クラフトの不等式を満たすことを条件として進めていくわ。クラフトの不等式を満たした上でLを短くするのが目標。(1)式の各符号語長をクラフトの不等式に代入できるように、l(i)からq(i)を以下のように定義するわ。
![]()
そして、このq(i)を利用して、クラフトの不等式を立てると以下のようになる。
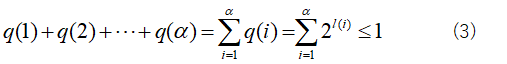
麦わら君
q(i)は符号の木では養分みたいなものと前回習いました。符号の木をイメージすることが大事ですね。あと(2)式からl(i)を求めると以下になりますね。

これって、前に習った情報の量みたいです。q(i)が確率p(i)なら情報の量ですね。
阿坂先生
そのとおりじゃ。後で勉強するがq(i)を確率p(i)に置き換えが可能で、この場合が平均符号長が最も短くなる。こうすると、符号語長=情報量となる。これは情報量が大きければ(発生確率が小さければ)符号語長も長くなるということじゃ。このことは何度も説明しているように、滅多に出ない記号は符号語長を長くし、頻繁にでる記号は符号語長を短くすれば良いということじゃ。
桂香助教
q(i)=p(i)がベストだってことをこれから導き出していくんだけど、出発点として以下の式から始めるわ。(logの底はいつものように2よ。)
![]()
阿坂先生
グラフを書くとこんな感じになるぞぃ。
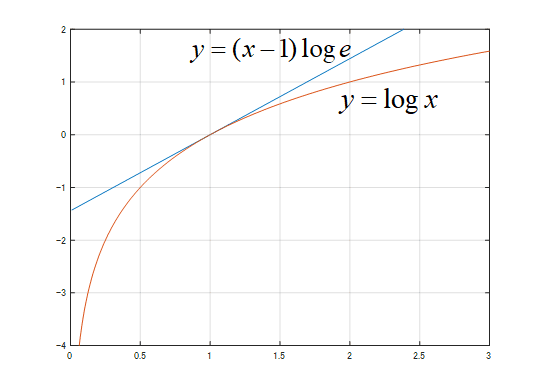
麦わら君
はい。(5)式の意味はわかります。でもこの式が何の意味があるのですか?
阿坂先生
ちょっとした魔法じゃ。まぁちょっと見ているのじゃ。ここでxにlog{q(i)/p(i)}を代入すると以下になるな。

p(i)は符号語l(i)が発生する確率とする。一応言っておくと、q(i)は(2)式だからlog{q(i)/p(i)}は正の値なので安心してlogの中に代入できるぞぃ。
麦わら君
はい。そうですね。でも、まだ式の意味がわかりません。
桂香助教
次に両辺にp(i)をかけるわ。

p(i)は確率(正の値)だから不等号の向きが反転することはないわね。さらにi=1,2,3,・・・,αまで全部足していく。このとき、どんなiであっても(7)式が成り立つから和∑をとっても不等号の向きは変わらないわ。

麦わら君
はい。何を目指しているのかわかりませんが、不等式は保たれていると思います。
阿坂先生
まぁ見ているのじゃ。ここで、(8)式の右辺を変形すると

となる。なぜ0以下になるかといえば、∑q(i)の部分は(3)式のクラフトの不等式を満たすように設計されるので1以下。それに対してp(i)は確率なので全部足せば1じゃ。だから、∑q(i)より∑p(i)のほうが大きいので、右辺は0以下じゃ。
麦わら君
ほうほう。
桂香助教
続いて(8)式の左辺よ。左辺は簡単よ。
![]()
となるわ。ここでlogq(i)は(4)式を使ってl(i)にしたわ。そして、∑p(i)l(i)は(1)式から平均符号語長Lだったわね。-∑p(i)logp(i)は何回も出てきたエントロピーHだわね。エントロピーの復習はここよ。
阿坂先生
だから(10)式と(11)式をまとめると
![]()
以下の関係になる。これが情報源符号化定理の言わんとしていることの1つじゃ。
桂香助教
平均符号語長LはエントロピーHよりも必ず長いという意味になる。頑張ればHに限りなく近づけられるというのもあるんだけど、それは後で勉強するわ。
麦わら君
おお!!!凄い。平均符号語長LはエントロピーHよりも大きくする必要があるんだ。これは感覚的にもしっくりきます。エントロピーが大きいとあいまいさが大きいので平均符号語長も長くなるってことか!これを証明したってことか。
桂香助教
クラフトの不等式の縛りが(9)式に入ってくることでH≤Lの関係となる。(11)式から平均符号語長Lを一番短い場合でL=Hとなることがわかる。これってどうゆう場合かというと、(9)と(10)式を見るとq(i)=p(i)であることが分かるわよね。
麦わら君
おお!!!なるほど。そうなると平均符号語長を一番短くするには各符号語長l(i)は(4)式から
![]()
という関係にすればいいのか!この式ってp(i)が小さい(確率が小さいほど)記号ほど符号長が長くなる。逆にp(i)が大きいほど記号ほど符号長が短くなる。
阿坂先生
この話は記号と符号語の割り当て方のときに話をしたな。つまり、出現確率が高い記号には短い符号を割り当て、出現確率が低い符号には長い符号を割り当てるということじゃ。
麦わら君
なーんだ。答えは結構簡単だったんだな。符号長は情報の量にすればいいのかぁ。これで完成ですね。
桂香助教
まだよ。話はこれで終わらない。問題の1つは(12)式は整数じゃないことよ。符号語長だから整数でしょ。(12)式を整数にしなくてはいけない。もう2つの問題は長さは分かっても具体的にどうやって符号化するか(0と1を割り当てていくか)を考える必要があるわ。
阿坂先生
整数じゃなければならない問題は簡単じゃ。-logp(i)の値を切り上げにすれば良いのじゃ。
![]()
⎡⎤は切り上げの記号じゃ。例えば、⎡1.46⎤=2じゃ。
麦わら君
理想的な符号長は小数点以下を含むのでちょっと妥協して整数nにするって訳ですね。符号語長が例えば2.345だったら3にするってことですね。
桂香助教
切り上げの意味は、小数点があった符号語を伸ばしたのと同じだわ。符号語長が伸びるということは、(3)式のクラフトの不等式は1未満を確保できる。(3)と(12)式から
![]()
の関係があり、クラフトの不等式を満たしていた。そして、切り上げた符号長n(i)はl(i)よりも大きいことから
![]()
となる。どのiの場合でも(15)式を満たすから和∑を取っても1以下になるのよ。クラフトの不等式は保たれる。
麦わら君
これは難しくはないですね。1つ目の問題はクリアしました。次は符号語をどうやって割り当てていくかですが、実際、どうやるのですか?
阿坂先生
色々な符号化方法が提案されているが、最も基本的なものを紹介しよう。まずは符号語は0からスタートする。一番短い符号語長が3ならば000からスタートじゃ。000から数字が増えていくイメージじゃ。
符号の木を考えてみよう。語頭条件を満たすためには、次の符号語は一つ頂点を遡ってそこから伸びていった先の葉とするか、もっと前の頂点に戻ってそこから伸びて行った先の葉にする必要がある。これは前に勉強した通りじゃ。これを図にしたのは下の図じゃ

桂香助教
ここで、符号語を2進数の小数点と以下と見なしてみるわ。このとき、少なくとも符号語0.000の次の符号語は0.001以上の符号語が必要だわ。(000は0.000、001は0.001よ。)どうしてかというと、0.000XXX・・・は上図の赤い符号語になっていて頭語条件を満たさないからよ。つまり、長い符号語が短い符号語を含むことになってしまう。そこで、次の符号は語頭条件を満たすために1個前かそれより前の頂点で分岐して、上図ように青の符号語である必要があるわ。
阿坂先生
このことをうまく式で表すことができれば機械的に符号化できる。まず、符号語長が短い順にB(1),B(2)・・・B(α)と並んでいるときに、次の符号語B(i)は元の符号語B(i-1)にその符号語の長さn(i-1)の2の-n(i-)乗の小数部を足せばよいことになる。
桂香助教
ちょっと複雑ね。具体例を出すわ。上記の例では、スタート(元)の000の符号語長が3であるので2の-3乗は0.125=0.001になり、元の符号語の小数部は0.000。0.000+0.001から次の符号は0.001⇒001だわ。次の符号語の符号長が4なら0010と書けるわ。
麦わら君
ちょっとややこしいですね。でも、このやり方はどんな場合でもうまくいくんですか?スタートの000はうまく行くのはわかりますが。例えば、B(i-1)が011の場合のB(i)はどうなるんですか?B(i)の符号長を4としてみます。。
桂香助教
B(i-1)=011の符号長が3だから2の-3乗は0.001となり0.011+0.001=0.100となる。B(i)は符号長が4だから1000となるのよ。

一般化して、式で書くと2進数の小数部分の計算ということにして
![]()
上式のように符号語をどんどん作って行ける。できた符号語の符号語長が足りない場合はお尻に0を追加してやって符号語を長くしてやればいいのよ。
麦わら君
あー 確かにこれなら頭語条件を満足しながら符号を作っていけそうです。でも、これって途中で小数部が0.111・・・11になってしまい、もうこれ以上符号語が作れないってことにはならないのですか?無理やり符号語を作ろうとして、後ろに0と足すやり方は語頭条件を満たさなくなるからできないですし。0.111・・・11000とかは駄目ですよね。
阿坂先生
それは良い質問じゃ。じゃが、お主の言っていることは、(16)式はα回繰り返すと2進数の小数部が1を超えてしまうのではないかということじゃな。その心配はない。クラフトの不等式から

という条件があったな。これは2の-n(i)の総和は1以下ということを示している。2の-n(i)乗というのは(16)式のものと同じじゃな。つまり、この総和は1以下になるってことじゃ。だから、小数点部分が0.111111111・・・が1.0001となってしまうようなことはない。つまり、1を超えることはない。
麦わら君
なるほど。符号語数が増えても小数点0.111・・・・11以内となる。符号語が枯渇してもう割当できないということにはならないのですね。
桂香助教
まとめると、符号化の仕方は以下よ。
① 記号を確率が大きい順に並べる。(符号長が短いものを先に作る)
② 各符号長を計算する n(i) = ⎡-log(p(i))⎤
③ 確率が一番大きい記号(一番短い符号)を符号化する。符号語は0を符号長n(1)だけ並べる。これをB(1)とする。
④ 2進数の小数部の計算でB(2) ← B(1) +2^(-n(1))
⑤ 以下、B(3)以降、B(i) ← B(i-1) +2^(-n(i-1))として繰り返す。
阿坂先生
では例題をやってみよう。以下を符号化してみよ。

麦わら君
まずは、①の確率順に並び変えて、②の符号長n(i)を計算すると以下ですかね。

桂香助教
まず、Eね。スタートは0からスタートするから符号長は2だから00だわ。そして次のBを計算するために符号長2から2の-2乗の小数部を計算しておくと01になる。

麦わら君
だからBの符号語は00+01で01か。符号長は2だからこのままだね。

同様に次のCを計算するために符号長2から2の-2乗の小数部を計算しておくと01になる。そして、符号語01+01を計算すると10になるけど、符号長は3だから100だね。

桂香助教
同様にして、すべてを計算したのが以下よ。

できた符号語の平均符号語長Lは2.55、エントロピーHは2.06よ。L>Hになっているわね。
阿坂先生
この符号化に似た符号化としてシャノンの符号化というのがあって、③2^(-n(1))の部分をp(i)の累積確率Cから符号化するものもあるぞぃ。今回はシャノンの符号化のやり方は省略して情報源符号化定理の完成を急ごう。
桂香助教
平均符号語長LはエントロピーHよりも大きくする必要があるけれども、一体、どこまで短くできるのか。ということを考えてみる。
阿坂先生
まず、式(13)より
![]()
符号長n(i)は情報量-logp(i)の切り上げじゃ。だから、n(i)は-logp(i)+1によりも小さくなる。
桂香助教
式(18)の左辺をエントロピーHに変換したい。なので、p(i)をかけて和を取ればエントロピーになる。

麦わら君
なるほど、平均符号語長LはH+1よりも小さいのかぁ。もっと小さくなることは可能なんでしょうか?
桂香助教
実際に上の表では平均符号語長Lは2.55、エントロピーHは2.06なので式(19)を満たしているわ。だけど、もっとLを短くできる方法がある。
阿坂先生
それが拡大情報源を使うことじゃ。拡大情報源というのは複数の記号を新たに1つの記号とする情報源じゃ。例えば、下の例でAとBを組み合わせABという新しい記号を作る方法じゃ、この場合、2つの記号の組み合わせたので2次拡大情報源という。例えば、以下のような情報源があったとき

2次拡大情報源は

となる。確率については連続して発生する確率を求めればよい。だから2つの記号の確率の掛け算で新しい確率が計算できるのじゃ。例えば、ABならばAの確率0.5とBの確率0.2をかけて0.1となる。
桂香助教
拡大情報源じゃない情報源と2次拡大情報源をそれぞれ符号化してみるわ。
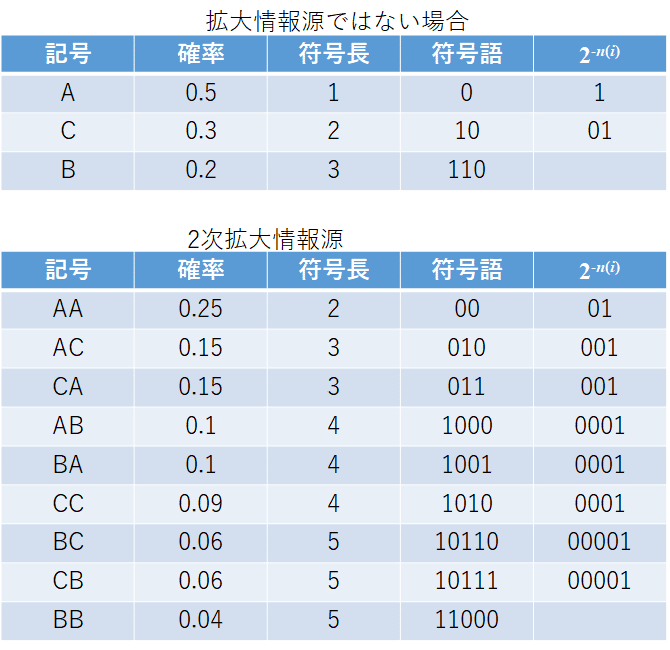
元々の情報源をそのまま符号化した場合の平均符号語長は1.7、2次拡大情報源の符号語長は3.36だけど、1つの符号語に2つの記号が含まれているから1個あたりの符号語長は3.36÷2=1.68となるわ。このように拡大情報源を使うと1記号あたりの平均符号語長を短くできる。
阿坂先生
(19)式は
![]()
じゃったな。これをn次拡大情報源に適用してみよう。n次にしても(19)式は満たされるはずじゃから、
![]()
になる。Hnはn個の記号を1つの記号と見なした時のエントロピーじゃ。Lnはn次情報源の平均符号語長を表すぞい。
桂香助教
ここで、Hnはn個の記号が含まれている場合のエントロピーだから、記憶のない情報源の場合、1記号のエントロピーをHとするとそのn倍となる。また、Lnはn記号の含まれて符号語長だから、1記号あたりの平均符号語長をLとすると、LnはLのn倍となる。以上から(20)式を書き直すと
![]()
となる。そして、上式をnで割ると
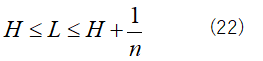
となる。
阿坂先生
ここで、nをものすごく大きい値にしてやるとどうなる?
麦わら君
1/nがとても小さくなりますから、LをほぼHにすることができますね。わかりました!!n次元情報源のnを大きい値にすればするほど、平均符号語長LはHに近づくんですね。
阿坂先生
そのとおりじゃ。(22)式から導かれる事実を情報源符号化定理と呼ぶのじゃ。これはシャノンの重要な定理の1つじゃ。シャノンの第1定理と呼ぶこともある。
桂香助教
(22)式は最初の不等号は平均符号語長LはH以下にすることは不可能ということを示しているのに対して、次の不等号は頑張ればHに限りなく近づけることができるということを意味しているのよ。
阿坂先生
もっとも、LがHに極めて近くなるためには大きいnが必要になり、上のnが増えるほど計算が大変になる。2次情報源でも計算が大変になったじゃろ。
麦わら君
なるほど。LはHに近づけることはできるけど、その分計算量が増えるんですね。Lをどこまで短くするかは計算量とのトレードオフってことですね。
阿坂先生
お主も分かってきたな。じゃが、今回、勉強した方法はあまり効率の良い符号化法ではないのじゃ。次回はハフマン符号というもっと効率の良い符号方式のやり方を勉強していくぞぃ。
桂香助教
念のため言っておくけど、ハフマン符号でも(22)式からの呪縛から逃れ慣れない。あくまでも今回勉強した符号よりも効率の良いやり方なの。それに、ハフマン符号にも拡大情報源が適用できるわ。
これから記事を増やしていく予定です。
