第14回　情報源符号化　その３(符号の木）

阿坂先生
今回は符号の木を勉強しよう。

桂香助教
前回勉強した語頭条件はややこしかったでしょ？符号の木を使えば符号が語頭条件を満たしているのかすぐにわかるのよ。

麦わら君
語頭条件とは長い符号語の先頭が短い符号語になっていないって条件でしたね。例えば、1101と11という符号語があって、符号語1101の先頭11がもう１つの符号11と同じなので語頭条件を満たさないってやつでした。

阿坂先生
そのとおりじゃ。でも、この語頭条件を満たしているのかいないのか調べるのは結構大変じゃ。1101と11の場合は一回調べれば終わりじゃが、符号語がたくさんある場合には１つずつ照合していては時間がかかる。

そこで、符号の木と呼ばれるのものがあるので紹介しよう。まずは言葉の定義じゃ。木には「根」と呼ばれる特別な「頂点」がある。これは言わばスタートポイントじゃ。

桂香助教
この根の頂点から2個の子頂点が伸びるのよ。子頂点からさらに2個の子頂点（孫頂点）というようにどんどんと木が成長していく。こんな感じよ。

阿坂先生
このようにどんどんと頂点を伸ばしていって完成された木について最後の頂点を「葉」といい、葉ではない頂点を「内部頂点」と言うぞい。

桂香助教
ここで、頂点は2分配されて成長していくって説明したでしょ。これはね、符号語でいうと2分配したものに０と１を割り当てていくことに相当するのよ。下のようにね。

そして、根から各葉まで辿ったルートを「道」と呼び、それぞれの道は各符号語に対応するわ。一番下の道は００００になるわよね。だからこの符号語は００００ということになる。

麦わら君
じゃあ、以下のような道ならば、符号語は００１ということですか？

桂香助教
そのとおりよ。あとは「木の高さ」を定義しておくわ。木の高さとは根から葉までの根を含まない頂点の数の最大値を示すわ。この例だと４になるわ。

麦わら君
なるほど。木の高さは最大の符号語長を示しているのですね。符号の木の定義については分かりました。ところで、この符号の木は何の役に立つのでしたっけ？

阿坂先生
符号の木を作ると先に言った語頭条件を満たすかどうかすぐわかる。語頭条件を満たす符号は瞬時符号なので、瞬時符号か非瞬時符号かを簡単に見分けることができる。語頭条件を満たさない符号は非瞬時符号じゃ。この瞬時符号か非瞬時符号の違いを覚えているかな？

麦わら君
もちろんです。瞬時符号は一意復号可能であり、つまり、一通りしか解釈（復号）できない符号であり先頭から解釈（復号）できる符号です。

桂香助教
符号語から符号の木を作ってみて、全ての符号語の終わりが葉であれば瞬時符号、内部頂点で終わるものがあれば非瞬時符号と分類することができるのよ。例えば、前回の表をもう一回出すわ。

まず、瞬時符号の符号４と符号５の符号の木を作ってみるわね。

麦わら君
確かに符号語がすべて葉で終わっていますね。

阿坂先生
つまり、すべて葉で終わるから瞬時符号。では非瞬時符号を見てみよう。非瞬時符号は符号３じゃったな。符号の木を書いてみると以下になる。

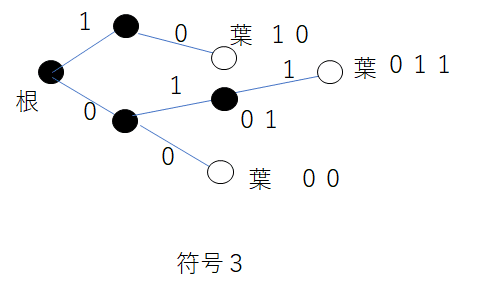
麦わら君
あっ　０１の符号語が葉ではないですね。内部頂点で終わっていて語頭条件を満たさない。だから非瞬時符号になるということですか？

桂香助教
そのとおりよ。前回の語頭条件を思い出してみて。語頭条件は長い符号語の先頭の部分が短い符号語になっているかどうかだったでしょ。だから、符号の木を書いてみると、長い符号語が短い符号語を含んでいるかどうか簡単に分かるわけ。

麦わら君
なるほど。語頭条件になっているかどうかは検索するのが大変ですが、符号の木を書けば条件に当てはまるかどうか簡単にわかりますね。

阿坂先生
この木の構造に関連して、クラフトの不等式というものがある。各符号語の長さをl(i)としたとき、以下の式を満たす場合は語頭条件を満足できる符号を作ることができる。

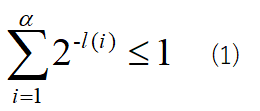
iは符号の番号じゃ。表１のように符号語が４つある場合はα=4でi=1,2,3,4じゃ。

桂香助教
式で書くと難しく見えるけど、計算自体は難しくない。簡単に理解するための例として木に養分を与えるとして例を考えてみるわ。まず、根に１の養分があるとする。その養分を根から内部頂点に向けて２分配するたびに半分づつ分け合っていくことを考える。そうすると下のような絵になるわね。

麦わら君
はい。なります。これががどんな意味あるんですか？

桂香助教
先へ行くほど養分がどんどん1/2になっていく。つまり符号語が1つ伸びる度に1/2になる。これが(1)式（クラフトの不等式）の２のl(i)乗に相当するわけよ。符号語長が伸びるたびに半減していくのが式（１）の２の－l(i)乗の部分。これらの総和が１以下からクラフトの不等式を満たすってわけ。

麦わら君
符号語の長さがl(i)でしたね。あ、そうか、各符号語のこの養分を足したものが（１）式なんですね。これが１以下なら語頭条件を満足するということか。符号語は2分配から作られるものだから(1)式はどうゆう場合でも1になるのではないですか？１にならないのはどうゆう場合ですか？

阿坂先生
例えば符号２じゃ。

となって、１を超えておる。

桂香助教
もう１つは枝分かれが半分しかないときよ。このときは語頭条件を満たすけど、ぴったり１じゃなくて1以下になるのよ。下の例では001に相当する符号語がないわ。

ちなみに、ぴったり１になる木のことを完全な木という。また、その符号を完全な符号と呼ぶわ。

麦わら君
わかりました。クラフトの不等式で１を超える場合は葉ではなくて内部頂点に符号が割り当てられている場合に発生しそうですね。この場合は非瞬時符号ですね。でも、符号語の数が少ない場合（符号語が2個とか）は内部頂点に符号語が割り当てられてもクラフトの不等式は満たす場合があるんじゃないですか？

阿坂先生
クラフトの不等式は達成可能な符号語長の下限を示しておる。ある符号が瞬時符号であるかどうかを判断するものでないことに注意が必要じゃな。瞬時符号つまり語頭条件を満たすかどうかは符号の木を見る必要がある。

桂香助教
作った符号が語頭条件を満たすかどうかは符号の木を作るのよ。そして、語頭条件を満たせばクラフトの不等式も当然満たすわよ。

阿坂先生
次回は最適な符号の作り方を考えていくぞぃ。