
ツケ払いで理解するデルタシグマ変調
「デルタシグマ変調は各サンプル点に対するPWM変調」という説明が上手く呑み込めずにいたが、bilibili動画で何気なくデルタシグマ変調を検索してみたところ何となくわかりそうなレベルで解説している動画を見つけたので(中国語はできないが、動画で映してる英語資料の説明が分かりやすかった)、自分の理解をnoteに残すことにした。
値段が中途半端なカフェの例え話
メニューが334円の「ブレンド」1つしかないカフェがあり、このカフェに毎日来てはコーヒーを1杯飲んで帰る常連客がいる。このカフェは現金しか使えないが、常連客も店主も小銭を持ち歩いたり取り扱ったりすることを極度に嫌っている。そこで、店主と常連客は以下のような取り決めをした。
常連客はツケ払いでコーヒーを飲む
現実世界であれば「ツケ」はお店を出るとき確定するが、今は例え話なのでコーヒーを注文した時点でツケが発生するものとする
帰り際にツケが250円を超えていたら常連客は500円を払う
ツケがマイナスになった分はプール金にして次回の支払いに当てる
プール金は便宜上「マイナスのツケ」として扱う
具体的に計算してみる。最初のツケは0だとする。
1日目、常連客がコーヒーを注文すればツケは$${0+334=334}$$円になり、250円を超えてるので帰るとき500円を支払う。
2日目、前日500円を支払ったためツケは$${334-500=-166}$$円になっおり、コーヒーを注文したら$${-166+344=168}$$円になる。250円以下なため客は1円も払わず帰る。
3日目、コーヒーを注文すればツケは$${168+334=502}$$円になる。客は500円を支払う。
4日目、前日500円を支払ったためツケは$${502-500=2}$$円になっおり、コーヒーを注文したら$${2+334=336}$$円になる。客は500円を支払う。
客が帰る直前、500円を支払うか支払わないか決める時点でのツケを「判定値」だとして、表に起こすと以下のようになる。
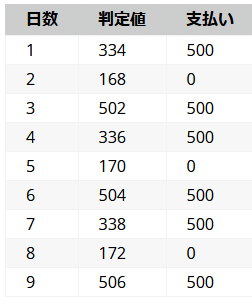
十分長い年月が経ったあと、常連客が実際支払った額の平均値、すなわち$${支払額の合計/日数}$$を求めるとその値はコーヒーの価格である334円に収束する。このことは直感的にも妥当である。

信号処理への適用
では上記のツケ払いのケースを数式で表現してみる。それぞれの値を次のように変数に割り当てる。
日数:$${i}$$
$${i}$$日目の判定値:$${det[i]}$$
$${i}$$日目の支払い額:$${pay[i]}$$
コーヒー代:$${coffee}$$ (=334)
初期値として、$${det[0]=pay[0]=0}$$とする。
$${i}$$日目の判定値は前日の判定値から前日の支払い額を引いて当日のコーヒー代を足した額であるため
$${det[i]\\ = det[i-1] - pay[i-1] + coffee\\= coffee - pay[i-1] + det[i-1]}$$
である。また、その日の支払額は
$${pay[i] = }$$if$${(det[i] > 250 )\ 500}$$ else $${0}$$
である。
この式を、$${pay}$$を出力とするブロック図に起こすと次のようになる。また、1bit ADCのブロックは入力が250より大きいか否かによって500か0を出力するブロックである。

このブロック図はまさにデルタシグマ変調のブロック図である。出力である$${pay}$$の遅延と入力$${coffee}$$の差を取る箇所が「デルタ」の部分で、$${det}$$の遅延と足す部分が「シグマ」に該当する($${det}$$を足し続けて総和を求めているので積分といえる)。
そして出力の$${pay}$$を平均化する=LPFに通すと、入力であるcoffeeが復元される。
$${pay}$$は平均をとったとき334になるような割合で500か0の二値のデータを含んでおり、1サイクル内でHIGHとLOWが複数回入れ替わるPWM変調といっても差し支えないと思われ、「デルタシグマ変調は各サンプル点に対するPWM変調」という言葉が理解できた。
また、この変復が成り立つためには入力が十分長い時間固定されている必要があり、デルタシグマ変調をする前に信号をオーバーサンプリングする理由も理解することができた。
