
フィッツの法則
グラフィカルユーザーインターフェース(GUI)の話です。
マウス操作において、クリックする対象が大きいほど素早く選択できる、クリックする対象が近いほど素早く選択できる、という法則です。


計算式
T = a + b log2 (D/W + 1)
T = 選択にかかる時間
D = ポインタと対象の中心までの距離
W = 対象の大きさ
a = ポインタ移動の開始・停止時間
b = ポインターの速度
フィッツの法則の応用例
Windows7ではデスクトップアイコンを選択するときに、アイコン上ではなくその周辺の領域もクリックできる様になっています。
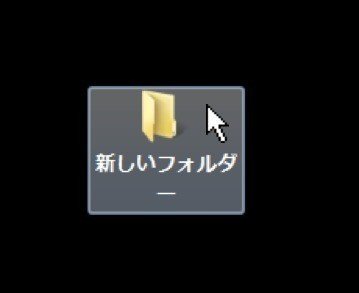
対象が大きくなった分、ポインティングが楽になります。
ポップアップウィンドウや右クリックのメニューはマウスの近くに表示されるため素早く選択できます。
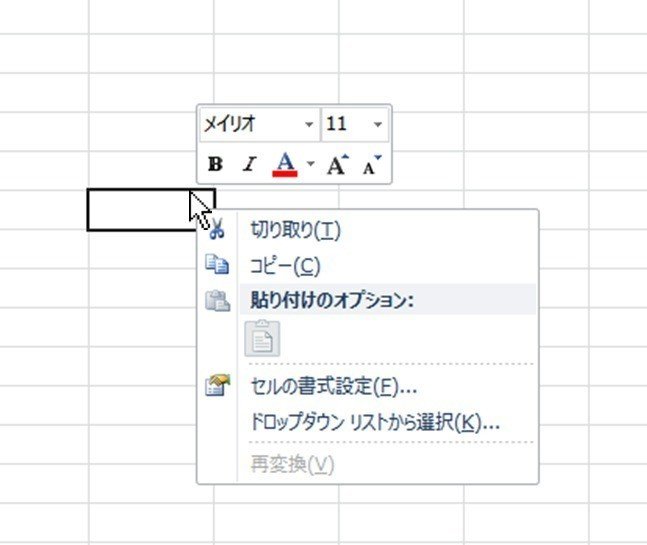
更に応用した例
画面の端はそれ以上マウスが進むことが無いため、事実上無限大の広さとなります。ウィンドウズ7やMacで使われています。

Windows7ではスタートボタンを選択するときにマウスを左下に持っていけばボタンの上にポインタが乗ります。マウスがスタートボタンを通り越し行き過ぎることがないため選択しやすいです。つまり無限大の大きさのボタンです。

また、右下はデスクトップを表示します。

Macでは画面の四隅にショートカットを割り当てることが出来ます。頻繁に行う操作を割り当てておけば、素早く作業を進めることができます。

大画面ディスプレイにおける問題
フィッツの法則を適用することにより作業効率を向上できます。しかし、大画面ディスプレイになると、マウス操作の距離移動は相対的に大きくなり、画面の四隅までの距離も遠くなっていきます。

そういう時にはジェスチャ操作などのショートカットが有効になります。詳細についてはジェスチャ操作の投稿で解説しますが、ジェスチャ操作はショートカット的な効果があるため移動距離を必要としません。Appleのマジックマウスやマジックトラックパッドはデバイス上でジェスチャ操作をできるので、大画面で作業をする時に効果を発揮します。
この様にフィッツの法則はGUI設計で操作効率を上げるために大いに活用できます。
詳しくはコチラ
https://ja.m.wikipedia.org/wiki/フィッツの法則
いいなと思ったら応援しよう!

