見出し画像

上がるの? 下がるの? 二値分類 AIを使って日経平均株価の予測に挑戦 まさかの結果編

日曜プログラマー

前回の記事より、今後の課題を振り返る

前回の記事で今後の課題としたものの中に、翌営業日の株価が上がるか下がるかのみを予測する二値分類を行うAIモデルの検証を挙げました。

そこで、今回は、適切な最後の活性化関数とロス関数を用いたAIモデルを使って、二値分類に挑戦してみることにしました。

二値分類を行う4層のAffineによるAIモデルの構成図

今回は、前回使用した4層のAffineによるAIモデルを流用することにしました。

ただし、二値分類を行うため、最後の活性化関数をSigmoid, ロス関数をBinaryCrossEntropyに置き換えました。

そのAIモデルの構成図が下記となります。

二値分類 4層 Affine AIモデル
二値分類を行う4層のAffineによるAIモデルの構成図

InputのSizeパラメーターを7, Affine_4のOutShapeパラメーターを2に変更しています。

その他のパラメーターはデフォルト値を使用しています。

学習データと評価データの作成方法

前回の記事で作成したExcelファイルを流用しつつ、学習データと評価データを作成していきます。

  • 学習データと評価データを作成する手順

    • Excelファイルでの処理

      1. 前回の記事で使用したExcelファイルを使用する

        • Excelファイルにはシートが2つある

          • ラベルを算出するシート

          • Min-Max正規化処理を行った数値が記載されているシート

      2. ラベルを算出するシートを選択する

      3. ラベルを置き換える

      4. Min-Max正規化処理を行った数値が記載されているシートを選択する

      5. 6種類のラベルを削除し、新たに作成したラベルをコピーする

      6. 作成したExcelファイルを保存する

      7. Min-Max正規化処理を行った数値が記載されているシートをcsv形式で名前を付けて保存する(以下、このcsvファイルを編集する)

    • csvファイルでの処理

      1. 1行目をx__0～x__6, y:labelに修正する

      2. 移動平均値およびラベルが欠損する行を削除する

      3. 一旦、csvファイルを保存する

      4. csvファイルをコピーし、1つを学習データ、もう1つを評価データとする

      5. 学習データの下位x行を削除し、csvファイルを保存する

      6. 評価データの下位x行を残し、上位の行を削除し、csvファイルを保存する

前回の記事で作成したExcelファイルにおいて、ラベルを算出するシートのデータが下記になります。

Excel 学習データ 基データ
前回の記事で作成したExcelファイルのデータ

そして、上記のExcelファイルでの処理において、ラベルを算出するシートに対して手順3までを行ったデータが下記となります。

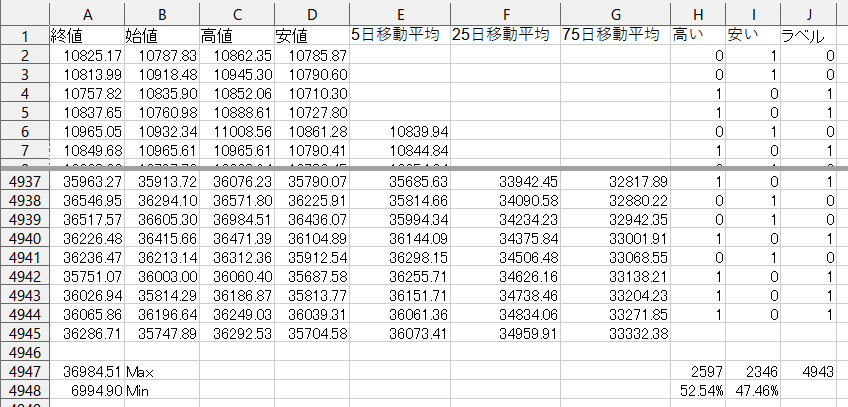
Excel 学習データ ラベル 修正データ
前回の記事で作成したExcelファイルに対してラベルを置き換えたデータ

前回の記事で作成したデータに対して、J～M列を選択し、列ごと削除します。

続いて、セルI1を「+1%越え」から「高い」に、セルJ1を「+1～+0.5%」から「安い」に変更します。

セルH2のラベルを算出する関数は、IF(A2<=A3, 1, 0)です。

セルI2のラベルを算出する関数は、IF(A3<A2, 1, 0)です。

セルJ2のラベルを算出する関数は、LOG(BIN2DEC(CONCAT(H2:I2)), 2)です。

セルH2, I2, J2の編集ができたら、セルH2, I2, J2の関数をコピーし、セルH3～J4944に貼り付けます。

そして、セルJ2～J4944をコピーします。

次に、Min-Max正規化処理を行った数値が記載されているシートを選択します。

セルH2を右クリックし、「形式を選択して貼り付け」メニューの「数値」を左クリックします。

一旦、Excelファイルを保存します。

以上で、上記のExcelファイルでの処理に対する手順6までが終了となります。

以後は、過去の記事に従って、学習データと評価データを用意します。

AIモデルの学習および評価を実行

上記のAIモデルを学習させた際の学習曲線を下記に示します。

二値分類 4層 Affine AIモデル 学習曲線
4層AffinのAIモデルによる二値分類の学習曲線

今回の学習では、学習曲線がほぼ平行であったため、Epoch(学習回数)を300としました。

ちなみに、Epochを500や1000にしても学習曲線は真横に伸びるだけでした。

どうやら、学習が正しく行われていないと思われます。

とりあえず、評価結果を確認することにします。

以下に、評価結果の混同行列を示します。

二値分類 4層 Affine AIモデル 混同行列
4層AffinのAIモデルによる二値分類の混同行列

y'__0の列が全てゼロとなっています。

つまり、AIモデルに予測してほしい値がlabel=0であろうが、label=1であろうが、とにかく、AIモデルはy'=1と予測したことになります。

株価予測に対して二値分類を行う場合、予測する結果は上がるか下がるかです。

このため、正解する確率はおよそ50%です。

実際、上記の結果では、Accuracy(分類精度)が54.11%となっており、これなら山勘と同じレベルです。

詳細を確認するため、AIモデルの評価データに対する出力を見てみることにしました。

二値分類 4層 Affine AIモデル 出力結果
4層AffinのAIモデルによる二値分類の出力結果(一部抜粋)

AIモデルの評価実行後の出力結果から、AIモデルが予測したy'__0の値は0.529前後で安定、y'__1の値は0.532前後で安定していることが確認できます。

どうやら、AIモデルの学習が私の期待するレベルよりもはるかに低い状態で安定してしまったようです。

その後、アレコレやってみたのですが、残念ながらこの状況から抜け出す方法が見つけられませんでした。

  • アレコレやってみた内容

    • AIモデルの変更

      • 層数、最後の活性化関数およびロス関数の変更

    • 正規化の有無による確認

    • 学習データと評価データの説明変数および目的変数の変更による確認

今後の課題

今後の課題は、二値分類の精度向上です。

とはいえ、思いつくことはアレコレやってみて、結果は変わらずだったので、二値分類に関する情報を集めたいと思います。

(参考までに)混同行列の見方について

AIに関する勉強のために本を読んでいるのですが、その本に混同行列に関する記述がありました。

イヌとネコの画像を二値分類する場合、正しく分類できることもありますし、その一方で誤って分類してしまうケースもあります。
このように、予測値と正解値との間にある関係を知るために混同行列(Confusion Matrix)というものが使われます。

金城 俊哉氏の著書『PC・IT図解 機械学習の技術としくみ』(秀和システム)

  • 混同行列の構成

    • ネコを陽(Positive), イヌを陰(Negative)とする

      • True Positive(TP): ネコを正しくネコと推測できている状態

      • True Negative(TN): ネコではないものを正しくネコではないと推測できている状態

      • False Positive(FP): イヌを誤ってネコと推測している状態

      • False Negative(FN): ネコを誤ってイヌと推測している状態

混同行列 構成表
混同行列の構成

  • Accuracy(正解率)の算出式

$$
Accuracy = \frac{TP+TN}{TP+TN+FP+FN}=\frac{TP+TN}{n(データ数)}
$$

  • Error Rate(誤答率)の算出式

$$
Error Rate=1-Accuracy
$$

  • Precision(精度)の算出式

$$
Precision=\frac{TP}{TP+FP}
$$

  • Recall(再現率)の算出式

$$
Recall=\frac{TP}{TP+FN}
$$

  • F1-Scoreの算出式

$$
F_1=\frac{2}{\frac{1}{Recall}+\frac{1}{Precision}}=\frac{2*Recall*Precision}{Recall+Precision}=\frac{2*TP}{2*TP+FP+FN}
$$

F1-Scoreは、F-Measuresと同じもののようです。


いいなと思ったら応援しよう！