
二値分類の過学習対策 AIを使って日経平均株価の予測に挑戦 データの隔たり確認編
前回の記事より、今後の課題を振り返る
前回は、翌営業日の日経平均株価が上がるか、下がるかを予測する二値分類に関して、過学習の状態に陥ってしまったことへの対策として中間層を4層Affine化したことによる効果を確認しました。
中間層を4層Affine化したことによる効果は、特になしという結論でした。
ただし、その過程において、学習データと評価データに隔たりがあることに気がつきました。
学習データと評価データの隔たりは、以下の通りです。
学習データと評価データの隔たり
学習データ
日経平均株価の値幅はおよそ7,000~31,000円
評価データ
日経平均株価の値幅はおよそ30,500~37,000円
つまり、日経平均株価がおよそ7,000~31,000円のデータを使用してAIモデルの学習を行っていました。
そして、学習済みAIモデルに対して、日経平均株価がおよそ30,500~37,000円のデータを使用して評価を行っていました。
今回は、こうした学習データと評価データの隔たりを極力抑えたデータを使用して、AIモデルの学習と評価を行います。
これにより、学習データと評価データの隔たりによる影響を確認します。
学習データと評価データの隔たりを極力抑える方法
両データの隔たりを極力抑える方法は簡単で、具体的には次の通りです。
学習データと評価データの隔たりを極力抑える方法
学習データを2分割する
前半の約4700-140日分のデータを新たな学習データとする
後半の約140日分のデータを新たな評価データとする
こうすることで、両データの隔たりは次のようになります。
新たな学習データと評価データにおける日経平均株価の値幅
新たな学習データ: 日経平均株価の値幅はおよそ7,000~30,800円
新たな評価データ: 日経平均株価の値幅はおよそ25,500~31,500円
AIモデルに使用したRNN LSTMの構造図
学習データと評価データの隔たりによる影響を確認するために使用したLSTMの構造図を下記に示します。

上記は、以前に作成したAIモデルで、中間層に1層Affineを使用したLSTMです。
AIモデルの学習および評価を実行
上記のAIモデルを使用した学習曲線と混同行列の比較を行うことにします。
比較対象は以下の通りです。
比較対象
パターン新: 隔たりを極力抑えた新学習データと新評価データを使用
パターン旧: 隔たりを押さえる前の旧学習データと旧評価データ
パターン新とパターン旧の学習曲線を以下に示します。


パターン新とパターン旧の学習曲線において、VALIDATION ERRORの振る舞いに違いを確認することができます。
特に、Epochが1000台で学習がリセットされたかのような挙動の後です。
パターン新は、VALIDATION ERRORが徐々に増加するのに対して、パターン旧は割とすんなりVALIDATION ERRORが増加しています。
また、VALIDATION ERRORの最小値に関しては、パターン新およびパターン旧での差はほとんど確認できませんでした。
続いて、混同行列を以下に示します。
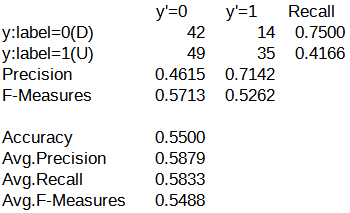
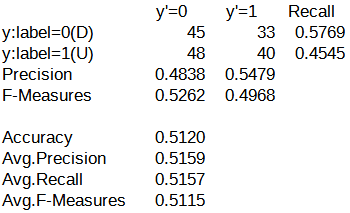
y'=0列に関しては、パターン新(Precision=0.4615)よりパターン旧(Precision=0.4838)の方が精度が若干高くなっています。
しかし、y'=1列に関しては、パターン新(Precision=0.7142)の方がパターン旧(Precision=0.5479)よりも精度が高くなっています。
二値分類としての精度は、パターン新(Precision=0.5500)の方がパターン旧(Precision=0.5120)よりも精度が若干高くなっています。
こうした結果から、学習データと評価データの隔たりによる影響について、あるともないとも言えない状況だと考えられます。
このため、LSTMの中間層にドロップアウトを追加したAIモデルを使用して、パターン新とパターン旧の差を確認することにします。
AIモデルに使用したRNN LSTMの構造図(中間層にドロップアウトを追加)
下記に、LSTMの中間層にドロップアウトを追加したAIモデルの構造図を示します。

AIモデルの学習および評価を実行(中間層にドロップアウトを追加)
LSTMの中間層にドロップアウトを追加したAIモデルを使用した場合のパターン新とパターン旧の学習曲線を以下に示します。


パターン新ではVALIDATION ERRORが徐々に増加していくのに対して、パターン旧ではVALIDATION ERRORが一定を保っています。
しかし、COSTとTRAINING ERRORに関しては、パターン新の方がパターン旧よりも低くなっています。
また、VALIDATION ERRORの最小値は、パターン旧の方がパターン新よりも低くなっています。
続いて、それぞれのパターンにおける混同行列を以下に示します。
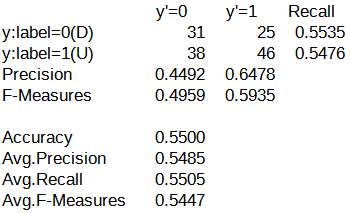
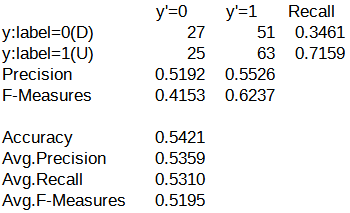
y'=0列に関してはパターン旧の方が精度が高く、y'=1列と二値分類としての精度はパターン新の方が高くなっています。
この特徴は、ドロップアウトを挿入しないAIモデルと同じです。
とは言え、学習データと評価データの隔たりによる影響について、あるともないとも言えない状況は変わらないというのが私の結論です。
自力がダメなら他力があるさ
どうしてもうまくいかないので、株価が上がるか下がるかを予測するAIに関する情報をインターネットで検索してみました。
そして、次の動画を発見しました。
キノコードさん作成の上記の動画は、Neural Network Consoleは使用しないものの、Pythonを使用して株価が上がるか下がるかを予測するAIの作成に関する解説を行っています。
キノコードさん作成の動画内容
月~木曜日の株価情報から金曜日の始値が上がるか下がるかを予測するAIモデルを作成する(動画11:50辺り)
各週の株価が、ある時は7,000円台だったり、またある時は25,000円台だったりするため、標準化と呼ばれる各週の株価の調整を行っている(動画16:40辺り)
AIモデルの構造はLSTMを使用している(動画17:30辺り)
作成したAIモデルの妥当性を検証するため交差検証と呼ばれる方法を実施している(動画21:20辺り)
過去の時系列データを使用して未来を予測する場合は、時系列分割による交差検証が一般的とのこと
今回作成したAIモデルはAccuracy=0.5152でした(動画25:40辺り)
私が作成した学習データは標準化を行っていませんので、この点は改善点として今後の課題としたいと思います。
標準化を行えば、今回取り上げたデータの隔たりに関する懸念は解決できそうです。
ところで、キノコードさんもLSTMを使用して、二値分類の精度が50%強であるため、私と同じ状況ではないかと考えられます。
もしかして、この辺りが限界なのかなとも思ってしまいました。
今後の課題
学習データと評価データに対して標準化を行い、今回使用したAIモデルでの確認を行います。
備考(古い株価データを取得する方法)
キノコードさんの動画で気になった点がありましたので、備考として記載します。
キノコードさんが使用していた株価データは、1965年1月5日から2021年10月21日までのものでした。
どうやって1965年のような古い株価データを取得したのかと疑問だったのですが、動画の下にある説明欄?に以下の記載がありました。
▼データセットについて 次のようにして事前に取得したデータを使用しています。
'''
import pandas as pd
import pandas_datareader.data as data
start = '1965-01-05'
end = '2021-10-21'
df = data.DataReader('^NKX', 'stooq', start, end) df.to_csv('finance_dataset.csv')
'''
上記のPythonコードから、Stooqというポーランドのサイトにアクセスすれば日経平均株価の古い株価データを取得することができるようです。
Stooqの左上にある「Symbol np: ^SPX」と記載された検索窓に^NKXと入力して「Kwotuj」ボタンを左クリックします。
すると、日経平均株価(Nikkei 225 - Japan)に関する情報が表示されます。
左下に「Historical data」とありますので左クリックすると、過去の株価データが表示されます。
「Start date」がMar/1/1914となっています。
そんなに古いデータが保存されているのかと思ったのですが、「Interval」にDailyを指定して表示させたところ、日足ではなく月足のデータが表示されました。
しかし、1960年代であれば日足のデータが表示されました。
Stooqを使用すれば、バブル期の最高値であった1989年12月29日の38,915円を含めた学習データが用意できそうです。
次回は、学習データの期間についても見直しをしたいと思います。
