
AIを使って日経平均株価の予測に挑戦 物語はまだ始まったばかり編
前回の記事より、今後の課題を振り返る
前回の記事で今後の課題としたものの中に、AIモデルが予測するラベル(AIモデルに予測させる分類)の偏りがありました。
具体的には、AIモデルに翌営業日の日経平均株価を予測させる場合において、予測するラベルが一部に偏っていました。
前回の記事では、予測する日経平均株価を次の3通りとしました。
当日の日経平均株価に関する情報に基づいてAIが予測する内容
翌営業日の終値が+1%を超えて上昇する
翌営業日の終値が-1%~+1%の間に収まる
翌営業日の終値が-1%を超えて下落する
上記に基づいた学習データのラベルに対する発生確率は、以下の通りです。
学習データのラベルに対する発生確率
+1%を超えて上昇: 19.56%
-1%~+1%の間: 63.28%
-1%を超えて下落: 17.16%
上記の場合、常に-1%~+1%の間を予測すれば約63%の正答率が得られます。
これでは、AIモデルをよりよく学習させることが難しいのではないかと私は思います。
そこで、今回は学習データのラベルに対する発生確率を平均化してAIモデルを学習させることとします。
また、前回は正規化処理としてNeural Network Consoleで用意されたBatchNormalizationを使用しました。
今回は、学習データにMin-Max正規化処理を行い、AIモデルを学習させることとします。
ちなみに、学習データへの適用内容は、必然的に評価データにも実施されます。
学習データのラベルに対する発生確率の検討
学習データの各ラベルを以下の2パターンとして期待値の発生確率を調べてみました。
パターンA: 予測する分類を5種類
翌営業日の終値が+1%を超えて上昇する: 19.56%
翌営業日の終値が+0.5%~+1%の間に収まる: 13.31%
翌営業日の終値が-0.5%~+0.5%の間に収まる: 38.26%
翌営業日の終値が-1%~-0.5%の間に収まる: 11.71%
翌営業日の終値が-1%を超えて下落する: 17.16%
パターンB: 予測する分類を6種類
翌営業日の終値が+1%を超えて上昇する: 19.56%
翌営業日の終値が+0.5%~+1%の間に収まる: 13.31%
翌営業日の終値が0%~+0.5%の間に収まる: 19.66%
翌営業日の終値が-0.5%~0%の間に収まる: 18.59%
翌営業日の終値が-1%~-0.5%の間に収まる: 11.71%
翌営業日の終値が-1%を超えて下落する: 17.16%
ラベルの発生確率として理想的なのはパターンBなので、今回はパターンBを学習データに使用します。
学習データにMin-Max正規化処理を実施
前回の学習データに対する懸念点として、AIモデルが出力するラベルが0~1であるのに対して、AIモデルに入力するデータが10000, 20000, 30000のオーダーなのは良いのだろうか、というのがありました。
結果的に、Neural Network Consoleで用意されたBatchNormalizationを使用したのですが、今回は、学習データにMin-Max正規化処理を実施します。
$$
y = \frac{x-x_{min}}{x_{max}-x_{min}}
$$
上記の式は、Min-Max正規化処理の公式です。
$${x}$$は正規化したい数値、$${x_{min}}$$は正規化したい数値グループの最小値、$${x_{max}}$$は正規化したい数値グループの最大値、$${y}$$が正規化処理後の数値です。
学習データと評価データの作成方法
それでは、早速、学習データと評価データを以下の手順に従って作成していきます。
学習データと評価データを作成する手順
Excelファイルでの処理
前回の記事で使用した仮の過去データを使用する
ラベルを今回の6種類に置き換える
各ラベルの発生数および発生確率を算出する(この手順はスキップしても良い)
ローソク足の過去データから最大値と最小値を算出する
新たにシートを挿入する
挿入したシートにMin-Max正規化処理を行った下記の数値を追加する
ローソク足(終値、始値、高値、安値)
5, 25, 75日移動平均値
追加したシートに6種類のラベルを追加する
作成したExcelファイルを保存する
追加したシートをcsv形式で名前を付けて保存する(以下、このcsvファイルを編集する)
csvファイルでの処理
1行目をx__0~x__6, y__0~y__5に修正する
移動平均値およびラベルが欠損する行を削除する
csvファイルをコピーし、1つを学習データ、もう1つを評価データとする
学習データの下位x行を削除し、ファイルを保存する
評価データの下位x行を残し、上位の行を削除し、ファイルを保存する
Excelファイルでの処理において、手順4までを行ったものが下記となります。

具体的には、日経平均株価の過去データを基に、5日, 25日, 75日移動平均値、6種類のラベル、各ラベルの発生確率、ローソク足の最大値と最小値を算出したものです。
各値の配置について
日経平均株価の過去データ: セルA2~セルD4945
5日, 25日, 75日移動平均値: セルE2~セルG4945
6種類のラベル: セルH2~セルM4944
各ラベルの発生数: セルH4947~セルN4947
各ラベルの発生確率: セルH4948~セルM4948
ローソク足の最大値: セルA4947
ローソク足の最小値: セルA4948
続いて、Excelファイルにおいて、6種類のラベル、各ラベルの発生数、各ラベルの発生確率、ローソク足の最大値と最小値を算出する方法を記載します。
6種類のラベルの算出方法
対照のセルをA2, A3とした場合の「+1%越え」ラベルを算出する関数はIF(A2*1.01<A3, 1, 0)です。
対照のセルをA2, A3とした場合の「+1~+0.5%」ラベルを算出する関数はIF(AND(A3<=A2*1.01, A2*1.005<A3), 1, 0)です。
対照のセルをA2, A3とした場合の「+0.5~0%」ラベルを算出する関数はIF(AND(A3<=A2*1.005, A2<=A3), 1, 0)です。
対照のセルをA2, A3とした場合の「0~-0.5%」ラベルを算出する関数はIF(AND(A3<A2, A2*0.995<=A3), 1, 0)です。
対照のセルをA2, A3とした場合の「-0.5~-1%」ラベルを算出する関数はIF(AND(A2*0.99<=A3, A3<A2*0.995), 1, 0)です。
対照のセルをA2, A3とした場合の「+1%越え」ラベルを算出する関数はIF(A3<A2*0.99, 1, 0)です。
対照のセルに従い、IF関数に与えるセルを変更します。
各ラベルの発生数の算出方法
対照のセルがH2~H4944である「+1%越え」ラベルの発生数を算出する関数はSUM(H2:H4944)です。
対照のセルに従い、SUM関数に与える範囲を変更します。
また、セルN4947は各ラベルの発生数の合計を表しています。
各ラベルの発生数の合計を算出する関数はSUM(H4947:M4947)です。
各ラベルの発生確率の算出方法
各ラベルの発生確率は、下記の式で求められます。
$$
各ラベルの発生確率 = \frac{各ラベルの発生数}{各ラベルの発生数の合計}
$$
このため、「+1%越え」ラベルの発生確率はH4947/N4947とし、セルの書式設定をパーセントに設定します。
対照のラベルに従い、分母のセルを変更します。
ローソク足の最大値の算出方法
ローソク足の最大値を算出する関数はMAX(A2:D4945)です。
ローソク足の最小値の算出方法
ローソク足の最小値を算出する関数はMIN(A2:D4945)です。
シートの挿入方法
新たにシートを挿入する方法は、使用するExcelのバージョン、等により変わってきます。
ここでは代表的な方法を記載します。
Excelの下部にシート名が表示されています。
シート名が並んでいる左か右に「+」マークがあれば、この「+」マークを左クリックします。
あるいは、並んでいるシート名の何れかを右クリックすると「シートの挿入」といったメニューが表示されますので、「シートの挿入」を左クリックします。
挿入したシートにMin-Max正規化処理を行った各数値を追加する方法
Min-Max正規化処理を行った状態を下記に示します。

挿入したシートの1行目は、基のシートの1行目をコピーしておきます。
また、基のシート名を「Orig」とします。
挿入したシートのセルA2には、次の関数を入力します。
($Orig.A2-$Orig.$A$4948)/($Orig.$A$4947-$Orig.$A$4948)
セルA4947には最大値が、セルA4948は最小値が保持されています。
また、「$」を付加すると、そのセルをコピー&ペーストしても位置を固定してくれます。
そして、セルA2をコピーし、A2~G4945の範囲にペーストします。
5, 25, 75日移動平均値の空白の範囲には、無効な数値が代入されますので、削除します。
次に、ラベルを挿入したシートに追加します。
元のシートである「Orig」のセルH2~M4944までの範囲をマウスで選択し、コピーします。
続いて、挿入したシートのセルH2を右クリックし、「形式を選択して貼り付け」メニューの「数値」を左クリックします。
以上で、Excelファイルの編集は終了ですので、ファイルを保存をしておきます。
次に、挿入したシートが選択されている状態で、「ファイル」メニューの「名前を付けて保存」を選択し、「ファイルの種類」でcsv形式を選択してファイルを保存します。
もし、文字コードを問われた場合は、「UTF-8」を選択しておけば問題ありません。
このcsvファイルから、学習データおよび評価データを作成します。
csvファイルを開き、1行目をx__0~x__6, y__0~y__5に修正します。
修正の具体例
セルA1の「終値」→ x__0
セルA2の「始値」→ x__1
セルG1の「75日移動平均」→ x__6
セルH1の「+1%越え」→ y__0
セルH1の「+1~+0.5%」→ y__1
セルM1の「-1%越え」→ y__5
ここで注意が必要な点は、ラベル名のルールがx__(アンダースコアが2個)n(nは0を含む自然数)であることです。
ラベル名がyの場合も同様です。
次に、移動平均値およびラベルが欠損する行を削除します。
具体的には、移動平均値が欠損する2~75行目と、ラベルが欠損する4945行目を行ごと削除します。
ここでcsvファイルを保存します。
次に、csvファイルをコピーします。
2つのcsvファイルの名前を学習データ用のファイルである「training.csv」と評価データ用のファイルである「evaluation.csv」とします。
「training.csv」を開いて、4701~4870(最終行)行を選択し、行ごと削除した後、ファイルを保存します。
続いて、「evaluation.csv」を開いて、2~4700行を選択し、行ごと削除した後、ファイルを保存します。
以上で、学習データと評価データの作成は終了です。
AIモデルの学習および評価を実行
今回使用するAIモデルの構成図は、下記となります。
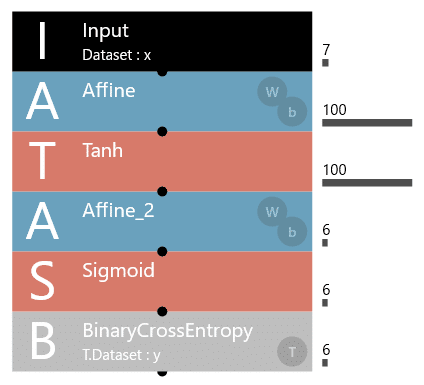
Input層のSizeパラメータは7に、Affine_2層のOutShapeパラメータは6に設定していますが、それ以外のパラメータはデフォルト値を使用しています。
また、前回の記事で使用していたBatchNormalizationは使用していません。
上記のAIモデルを学習させた際の学習曲線を下記に示します。
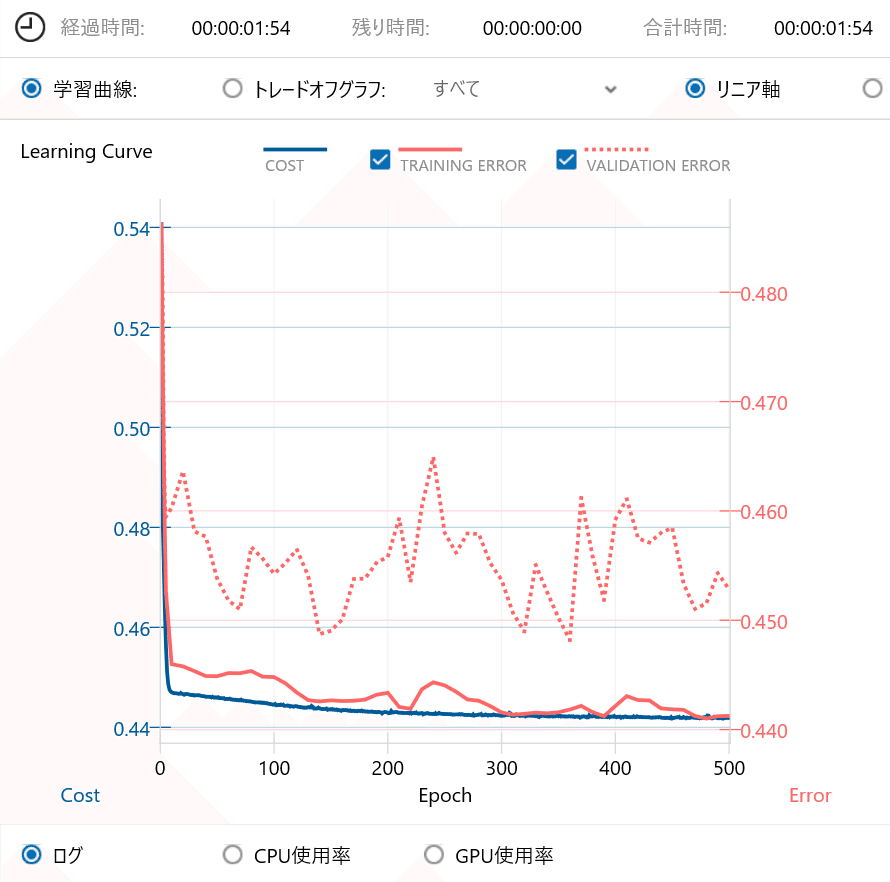
今回の学習では、学習曲線を収束させるためにEpoch(学習回数)を500としました(前回は100)。
ちなみに、私のPC環境(Intel 第7世代Core-i5 CPU + 4GByteメモリ)では、今回のAIモデル構成でEpochが500だと学習時間は1分54秒でした。
それでは、評価結果を以下に示します。

ラベルを6種類とした状態でAccuracy(分類精度)が18.82%なので、かなり分類精度が低いことが確認できます。。
上記の混同行列を見ると、y'__1, y'__3, y'__4およびy'__5の列が全て0となっています。
これは、全てラベルのケースでy'__1, y'__3, y'__4およびy'__5は予測されなかったという意味です。
私の経験不足のため、なぜ、このような結果になるのかは分かりません。
この点は、今後の課題としたいと思います。
それから、Min-Max正規化処理に関してですが、今回はBatchNormalizationを使用することなく、AIモデルの学習が進みました。
やはり、学習データに対する正規化処理は必要だと私は理解しました。
今後の課題
今回の評価は、期待値が均等になるようにバランスを取った6種類のラベルでAIモデルの学習を行いました。
しかし、評価結果から活性化しないラベルが存在することが確認できました。
この点について、より複雑なAIモデルを使用することが解決策になるか、検証する価値があると思います。
また、期待値を均等にする目的で、翌営業日の日経平均株価が上がるか下がるかを予測させるAIモデルの検証もやってみたいと思います。
AIモデルのデータについて
今回作成したAIモデルのデータは、Googleドライブにて共有しています。
GoogleドライブURL: https://drive.google.com/drive/folders/1zB4oko_et0OoESRuTPhi2eHhf4Hb0bjR?usp=sharing
N225_Simple2Layer_NormData_1.sdcproj
Neural Network Console用のプロジェクトファイル
