
二値分類の過学習対策 AIを使って日経平均株価の予測に挑戦 中間層を4層Affineにしてみた編
前回の記事より、今後の課題を振り返る
前回は、翌営業日の日経平均株価が上がるか、下がるかを予測する二値分類に関して、過学習の状態に陥ってしまったことへの対策としてドロップアウトの効果を確認しました。
過学習対策としてのドロップアウトの効果は確認できました。
しかし、期待していたVALIDATION ERRORを低下させる効果は確認できませんでした。
そこで、過学習を抑え、かつ、VALIDATION ERRORを低下させる目的で、今回はAIモデルの中間層を4層Affine化してみることにしました。
AIモデルに使用したRNN LSTMの構造図
中間層を4層Affine化したLSTMの構造図を下記に示します。

上記のAIモデルにおいて、Affine_M1~Tanh_M4までが今回変更した中間層になります。
上記のAIモデルの構造を基本としつつ、また、過学習への対策も考慮した結果、中間層の構造を下記のパターンA~Eとして学習および評価を行いました。

パターンA~Eの構造は、次の通りです。
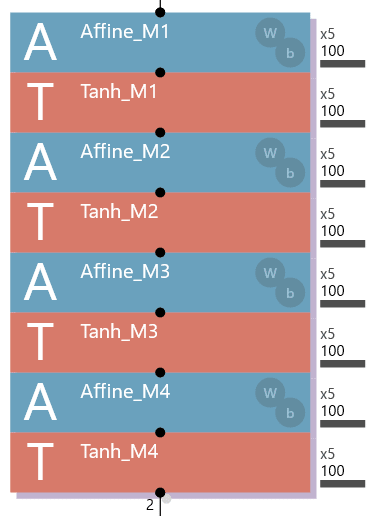
パターンA~Eの構造
パターンA: 4層Affineの構造のみでDropoutは未使用
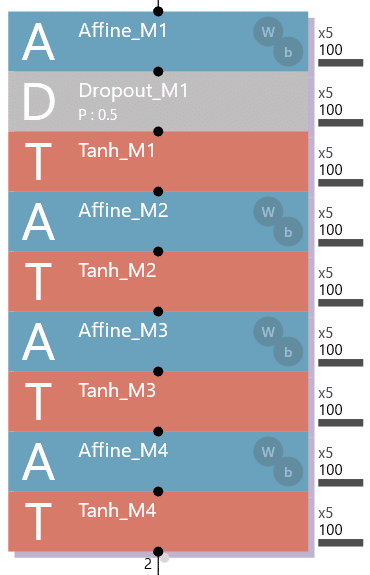
パターンB: 4層Affineの構造で、Affine_M1の直下にDropout_M1を追加(全体でドロップアウトを1つ使用)
パターンC: 4層Affineの構造で、Affine_M2の直下にDropout_M2を追加(全体でドロップアウトを1つ使用)
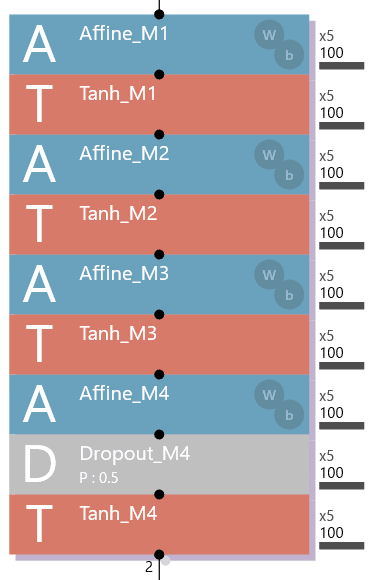
パターンD: 4層Affineの構造で、Affine_M4の直下にDropout_M4を追加(全体でドロップアウトを1つ使用)
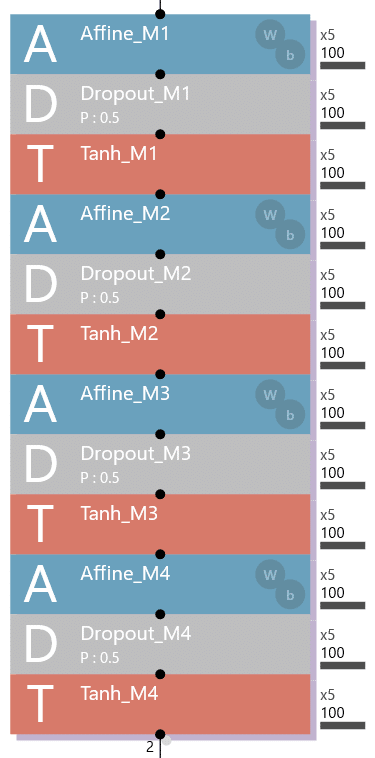
パターンE: 4層Affineの構造で、各Affineの直下にDropoutを追加(全体でドロップアウトを4つ使用)
ドロップアウトのパラメーターは全てデフォルト値(P=0.5)としています。
また、学習および評価データは、前回使用したものをそのまま使用しました。
AIモデルの学習および評価を実行
パターンA~Eでの学習曲線を下記に示します。


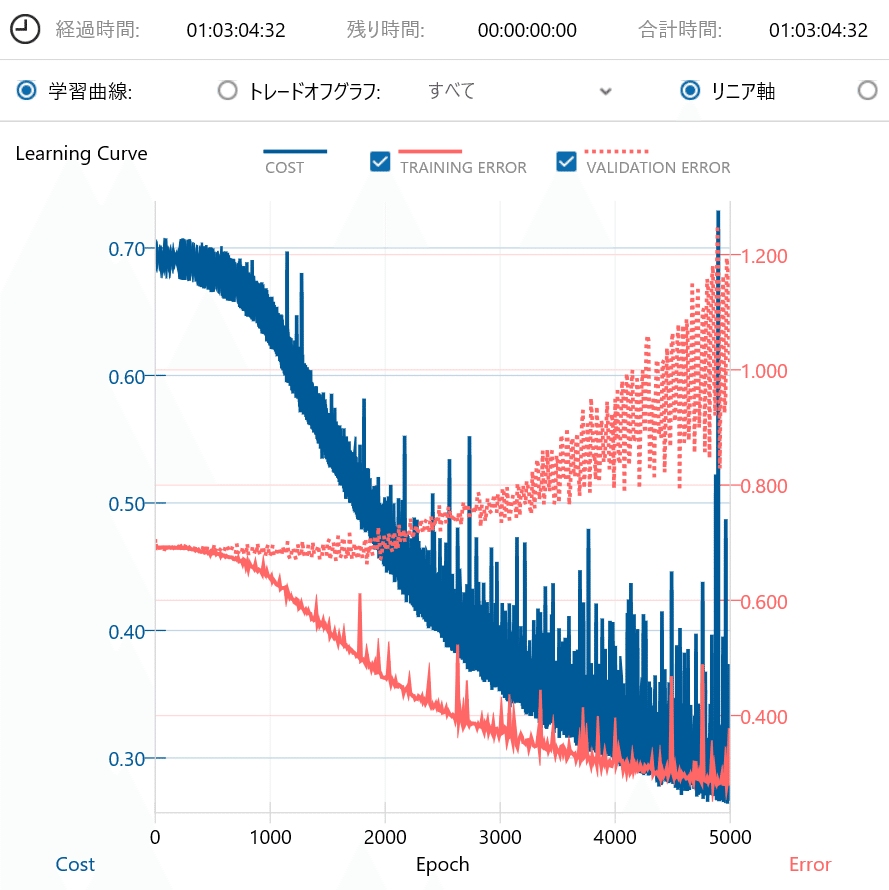


パターンAの学習曲線は、学習の途中でリセットされたかのような、ドロップアウトを使用しない場合に見られる特徴が確認できました。
ドロップアウトを1つ使用するパターンB~Dの学習曲線は、ドロップアウトの挿入位置を上位層から下位層に移動するにつれてVALIDATION ERRORも低下していくことが確認できました。
パターンEの学習曲線は、COSTとTRAINING ERRORに追従するように、VALIDATION ERRORが低下しているように見えます。
期待通りの結果が得られそうな予感がしましたが、混同行列を確認するとそうでもありませんでした。
続いて、パターンA~Eの評価結果における混同行列を以下に示します。
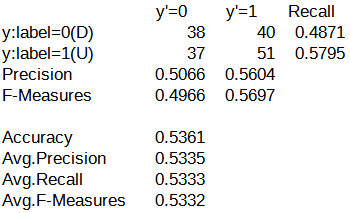
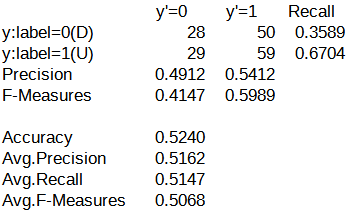
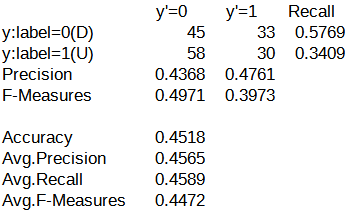
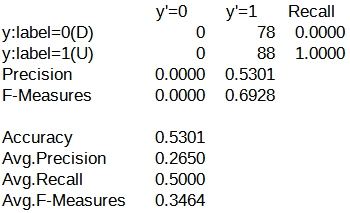
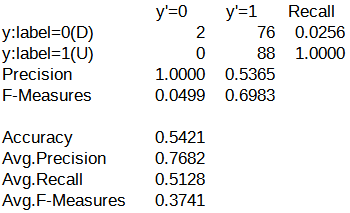
混同行列を確認したところ、y'=0列(翌営業日の日経平均株価が下がる)の予測がされたケースと予測されなかったケースの2つに分かれていました。
パターンA~Cでは、y'=0列を対象とした予測が行われていました。
一方で、パターンD, Eでは、y'=0列を対象とした予測がほとんど行われていませんでした。
過去の検証結果では、y'=0列、あるいは、y'=1列の予測がされない状況、つまり、どちらか一方に予測が偏ってしまう状況は、LSTMの構造を使用しないケースで散見されました。
こうした結果から、ドロップアウトは最終層に挿入すると、LSTMの効果である過去の記憶を打ち消してしまう可能性があると推測されます。
過学習に対する考察
これまでいろいろと検証してきましたが、Accuracy(分類精度)が55%程度で頭打ちとなる状況が続いています。
裏を返せば、VALIDATION ERRORが0.68程度で下限となる状況です。
学習曲線からは過学習が確認されているため、過学習への対策をアレコレ行ってきました。
改めて、過学習の主な要因をインターネットで調べたところ、次の通りです。
過学習の主な要因
学習データの不足や偏り
AIモデルの選択が不適切
学習データに関しては、不足を疑い、ボリンジャーバンドやMACDを追加しました。
また、AIモデルに関しては、これまでの検証結果から、株価予測にはLSTMの構造が適しているという感覚を得ることができました。
ここで気になるのが、学習データの偏りです。
学習データと評価データは、日経平均株価のローソク足データを加工して用意しています。
参照している日経平均株価の期間は、2004年1月5日から2024年1月31日までとなります。
学習データと評価データの内訳
学習データ
前半の約4700日分(およそ2004年5月~2023年5月)
日経平均株価の値幅はおよそ7,000~31,000円
評価データ
後半の約140日分(およそ2023年6月~2024年1月)
日経平均株価の値幅はおよそ30,500~37,000円
今更ですが、学習データと評価データの間に大きな隔たりがあるような気がします。
しかし、上記の隔たりが問題となるなら、右肩上がりで変化する何かをAIモデルで予測することは困難となりそうです。
ですが、流石にそんなことはないような気がします。
ふと、学習データと評価データの隔たりについて、影響を確認する方法を思いつきました。
学習データと評価データの隔たりによる影響を確認する方法
学習データを2分割する
前半の約4700-140日分のデータを新たな学習データとする
後半の約140日分のデータを新たな評価データとする
この場合、新たな学習データと評価データにおける日経平均株価の値幅は次のようになります。
新たな学習データと評価データにおける日経平均株価の値幅
新たな学習データ: 日経平均株価の値幅はおよそ7,000~30,800円
新たな評価データ: 日経平均株価の値幅はおよそ25,500~31,500円
現状よりは、学習データと評価データの隔たりが解消されると考えられます。
今後の課題
新たな学習データと評価データを使用することで、日経平均株価の値幅に対する隔たりの影響を確認します。
使用するAIモデルは、条件を簡素化する目的で、以前作成した中間層を1層のAffineとするLSTMを使用します。
AIモデルのデータについて
今回作成したAIモデルのデータは、Googleドライブにて共有しています。
URL: https://drive.google.com/drive/folders/1Gzlp4AjWt2Z7ttBIwKqJT9_-P7dapVaP?usp=drive_link
N225_LSTM_4Affine100N_BB-MACD_5Days.sdcproj
Neural Network Console用のプロジェクトファイル(パターンA)
N225_LSTM_4Affine100N_Dropout-1_BB-MACD_5Days.sdcproj
Neural Network Console用のプロジェクトファイル(パターンB)
N225_LSTM_4Affine100N_Dropout-2_BB-MACD_5Days.sdcproj
Neural Network Console用のプロジェクトファイル(パターンC)
N225_LSTM_4Affine100N_Dropout-4_BB-MACD_5Days.sdcproj
Neural Network Console用のプロジェクトファイル(パターンD)
N225_LSTM_4Affine100N_Dropout_BB-MACD_5Days.sdcproj
Neural Network Console用のプロジェクトファイル(パターンE)
