
カレンダー計算の極意
講師:常勝のポストペロブスカイト(上部画像参照)

カレンダー計算に必要な数式
a1 = (xxxxxxxxcc mod 4 * 5) mod 7([ ]はガウスの記号)
a2 = (yy + [yy / 4]) mod 7([ ]はガウスの記号)

a3a = ([(mm + 2)* 30.6 + 0.5] mod 7 + 3) mod 7 (平年3月以降)
a3b = [(mm + 14)* 30.6 + 0.5] mod 7 + 2 (平年1月2月)
a3c = [(mm + 14)* 30.6 + 0.5] mod 7 + 1 (うるう年1月2月)
([ ]はガウスの記号)

a4 = dd mod 7

weekDay = (a1 + a2 + a3 + a4) mod 7
各種数式の解説
最初にa1~a4までの数式について簡単な説明をしておこう。
まず、a1の数式が成り立つ、ってのが何を意味するか分かるか?
a1 = (xxxxxxxxcc mod 4 * 5) mod 7([ ]はガウスの記号)

これはグレゴリオ暦の「年」周期が一般によく言われる「28」年周期とかじゃなくて、確実に「100」年周期であることを意味している。
それと同時に、年数の下4桁以外、要するにxxxxxxxxの部分がどんな値をとっていても計算結果には一切影響しねえ、ってコトをも意味している。
実際、2028年05月28日が日曜日なら、1234567892028年05月28日も9876543212028年05月28日も、その他のxxxxxxxx2028年05月28日も必ず日曜日になる。
xxxxxxxxccyymmddのxxxxxxxxxxの部分については一切計算する必要がねえ。
「えっ、そんな訳ねえだろ?」とか思っちまったテメエはどんな計算方法でもいいからまずは自分で計算して確かめてみろ。
最終的にはコレを理解できるかできねえかがカレンダー計算を極められるか極められねえかの境界になる。
逆の言い方をすると、これが理解できねえ限りは前後40000年とかそのくれえの範囲しか計算できねえ。
まあオレからすると前後40000年が計算できてた時点で前後1億年後でも前後10億年後でもとりあえず答えは出せたんじゃねえの?って思うんだけどな。
過去の論文に「前後4万年(計8万年)が計算できる症例者がいた」と書いてある。
これは少なくとも医者(恐らくは博士)が書いているはずなんだが、結局は本人も周りの連中も誰1人としてカレンダー計算の真実に気がつかなかった、ってことなんだろう。
もちろん28年も28年で周期であること自体は否定しない。
周期っていうのはどこからどこまでの範囲で区切るかって問題でもあるし、とりあえずでも何回かの繰り返しがあることもまた事実だからな。
ところで実をいうとグレゴリオ暦はうるうに関する規定が超適当だ。
うるう日とうるう年の扱いがごっちゃになっちまってるし、36524日周期の外に存在している「うるう世紀」までうるう年として扱っちまってる。
しっかりしろよ教皇!とか言っちまうとゼッテー火あぶりにされるからとりあえず言わねえでおくが、現実としてグレゴリオ暦の規定は
4で割れる年はうるう年、ただし100でも割れる年は平年
ただし100で割れても400で割れる年はうるう年
となっている。
このグレゴリオ暦の規定に対する解釈をちょっと変えて、
4で割れる年はうるう年、ただし100でも割れる年は平年
4で割れる世紀は「必ず」うるう世紀
と考えてみろ。
4で割れる年は366日、ただし100でも割れる年は365日、ってことは、100年の日数が「必ず」36524日になる、ってことになるわけだから、これが完全に完成した1つの周期になる。
そして100年=1世紀の日数が36524日で完全に完成した1つの周期を形成している以上、36524 mod 7 = 5なんだから1「平」世紀分の日数36524日が進むと曜日は必ず右方向に5日分ずれる。
そして1うるう世紀は1平世紀 + 1うるう日 = 36524 + 1日。
うるう世紀は「4世紀に1度確実に」やってきて、ここに例外はねえワケだから、うるう世紀の日数は「必ず」36525日、うるう世紀の曜日移動量は36525 mod 7 = 6になる。
さらに言うなら例外がねえ以上グレゴリオ暦ではこの5日5日5日6日の曜日移動が4世紀1セットで延々繰り返されることになるわけだから、(5 + 5 + 5 + 6) mod 7 = 0で、4世紀に一度、曜日移動量は「必ず」0になる。
この「4世紀に1度『必ず』0になる」って部分が重要で、残りの3回は必ず右に5日分ずれるわけなんだから、結局この関係式はa1 = (xxxxxxxxcc mod 4 * 5) mod 7っていう形で表せる。
まあ36524 + 36524 + 36524 + 36525 = 146097日も完全に完成した1つの周期を形成して、しかも7で割り切れるわけなんだから、当たり前って言えば当たり前のことではあるんだがな。
「周期がある」ってことは、つまりはそういうことなんだからよ。
結果、2028年05月28日が日曜日なら2428年05月28日も2828年05月28日も3228年05月28日も9628年05月28日もみんな日曜日だし、2128年05月28日や5328年05月28日は右に5日分動いて金曜日、2228年05月28日や8628年05月28日は右に3日分動いて水曜日、2328年05月28日や5528年05月28日は右に1日分動いて月曜日、ってことになる。
あと、これもやっぱり大半のヤツにはわからねえみたいなんだが、うるう年ってのは本来4年に1度じゃなくて5年に1度と数えるべきだ。
もちろんうるう世紀も4世紀に1度じゃなくて5世紀に1度と数えるべきだな。
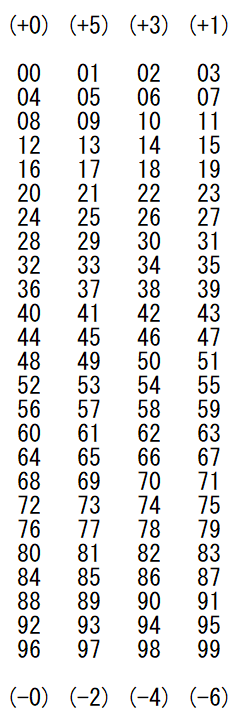
天体の動きとかガン無視で数値の動きだけ見てみればわかるんだが、たとえばa2解の表を見ると横に見た場合だけじゃなくて縦に見た場合でもやっぱり5回に1回空白が出てくるだろ?
これは真のうるう年の周期5と週の周期7が35の周期で調和していて、そのうち7回うるう年が削除された結果としての28と、グレゴリオ暦が言うトコのうるう年の周期4が調和するからこそ起きる現象だ。
そしてこれは結局のところ1年が365日であろうと366日であろうとやっぱり平年は平年で、うるう年はうるう年としてたとえ0日であっても別に存在しなくちゃならねえことを意味しているわけなんだが、結局
真のうるう年はマイナンバーを持つことさえ許されず闇に葬られた。
暦ってのは地球の公転回数と経過年数とを合わせりゃそれでいい、ってものじゃねえはずなんだがな。
そもそも「平年に1日を追加して366日のうるう年にする」なんて取り決めからしてもうメチャクチャだと思わねえか?
地球だっていつまでも同じ速度で回り続けられるワケじゃねえんだし、あと1億年もしたら普通に分かるようになるとは思うんだが、その頃の地球はどんなにがんばっても365回転なんてできなくなっちまってるハズだ。
その公転軌道上には「366日目」なんて存在する余地がねえ。
つまり、本来のうるう年は「365日に1日を追加した366日の年」とかじゃなくて、「365日から364日が消えた1日の年」であるべきなのさ。
だから本当に削除されるべきも実際に存在するうるう年の方じゃなくて、この存在しねえ364日の方だったハズだ。
それでこの364日が消えちまうコトに何か問題があるんだったとしたら、その364日を補償して365日分と数えたらそれでよかった。
実際1年を0のねえ365進数として数えてみたら分かるハズなんだが、365が過ぎて366になる時、繰り上がりの部分が「1」になるだろ?
そして次の365が過ぎたらもう一度繰り上がってその部分が「2」になる。
すると365 mod 7 = 1かつ1 mod 7 = 1なんだから、もしもうるう年に正しく1年として1日が与えられ、364日を補償して365日だったものとして数えることができていれば、この繰り上がった数値の部分が年数と曜日のズレとを同時に兼ねて示していたハズだ。
そうすればうるう年のたびに曜日の動きがとびとびの値を取る必要なんてどこにもなかったし、カレンダー計算がここまで複雑になることもなかった。
まあほとんど同時にユリウス通日とかつくってたヤツもいるワケだし、別にかまわねえって言えばかまわねえんだけどな。
オレは地球の公転については回転運動じゃなくて螺旋運動だと思ってるし、だから究極的には自転も合わせた上でグリニッジ天文台の直線運動に置きかえたりとかもするんだが、これを数値化すると実質的にはユリウス通日と同じものになる。
時間の基準が「1正午」だからな。
これが何を意味するのかって言うと、太陽と地球の位置関係がどれほどに破綻しようが「ユリウス通日」と「曜日」の関係は絶対にずれねえ、ってコトだ。
つまり季節のズレとか公転周回数とかを気にせず正午の回数だけに焦点をあてて考えた場合、たとえ地球の自転回数が31557600秒間で360回をきっちまったとしても、365正午とか366正午を1年と数えればいいワケだから、グレゴリオ暦の規定に従っての10億年後の曜日はちゃんと計算するコトができる。
どうせどこかで改暦されるんだろうし、意味のねえ話ではあるんだがな。
そのくれえの時代になっちまうと、酸素呼吸できるのかどうかも分からねえし。
何にしてもa1の数式が成り立つ以上、a2の値は100年周期の値になるわけだから、a2の並びについては21xx年代でも25xx年代でも99xx年代でも絶対に変わらねえ。
a2 = (yy + [yy / 4]) mod 7([ ]はガウスの記号)

そしてこの縦列の並びは、日付さえ同じなら曜日もぜんぶ同じだから、2028年05月28日が日曜日なら、2000年05月28日も2006年05月28日も2017年05月28日も2023年05月28日も2034年05月28日も2045年05月28日も2051年05月28日も2056年05月28日も2062年05月28日も2073年05月28日も2079年05月28日も2084年05月28日も2090年05月28日もみんな日曜日、ってコトになる。
でも01月と02月の時はうるう年のせいで曜日ズレるんじゃねえのか、って?
まあ「曜日」はな。
だがa2の値はズレねえんだよ。
そもそも論としてa1とa2の値はxxxxxxxxccyy年の部分の「曜日移動量」であって「曜日」そのものじゃねえ。
a2の値がいくつになるのかってコトとyy年がうるう年であるかどうかってコトもまったく別の問題になる。
うるう年で曜日がずれるってのは「02月29日」が存在するからなわけで、そっちは万年計算じゃなくて年内計算の領域なんだよ。
言葉で説明されてもよく分かんねえヤツは、この世界のクソゲーの中でも最もクソゲーと評されるであろうゲーム、
をやってみるといい。
コイツをマトモにクリアできるヤツは世界に10人といねえハズだが、別にクリアはできねえでも、何度計算してもa2の値は絶対にずれねえ、ってコトくれえは分かるようになるだろう。
むしろこのゲームはうるう日を計算の外にはじいているから、a3の値すらずれねえ。
それでも計算が成り立つのはa1とa2で外枠を固めてあるからだ。
オレの解法だとうるう年が何回来てるとかはまったく関係ねえんだよ。
まあ何にしても21xx年代になると「a1」の値が+5になるから、結果として「曜日」も5日分右に動く。
つまり、この時a1 + a2の値は5 + a2ってコトになるから、
5 + a2 = ((yy + [yy / 4]) mod 7 + 5) mod 7([ ]はガウスの記号)

みてえな感じになる。
前のa2表と値の並びそのものは変わらず、( )内の値だけが変わったんだが分かるか?
それで2128年05月28日が金曜日になるから、2100年05月28日も2106年05月28日も2117年05月28日も2123年05月28日も2134年05月28日も2145年05月28日も2151年05月28日も2156年05月28日も2162年05月28日も2173年05月28日も2179年05月28日も2184年05月28日も2190年05月28日もみんな金曜日、ってコトになる。
もちろん下2桁年の並び09、15、20、26、37、43、48、54、65、71、76、82、93、99、は一切変わらねえ。
まあa2表については途中で計算するのがめんどうになって縦書きしながら覚えちまおうってヤツも出てくるんじゃねえかとは思うが、それならそれで別に構わねえ。
この世界には使っているうちに自然と理解できるようになる概念ってヤツもある。
結局は理論を先に覚えるか値を先に覚えるかの違いにしかならねえ。
続いてa3の説明に入るが、テメエらうるう日のある2月~3月間以外の月間曜日差は固定値だ、ってコトは知ってるか?
まあ月の日数が固定値なんだからその曜日差も固定値になるのは当たり前って言えば当たり前のことではあるんだが、とりあえず1月1日と2月1日の曜日差は右に3日、2月1日と3月1日の曜日差は右に0日または右に1日、3月1日と4月1日の曜日差は右に3日、4月1日と5月1日の曜日差は右に2日、5月1日と6月1日の曜日差は右に3日、6月1日と7月1日の曜日差は右に2日、7月1日と8月1日の曜日差は右に3日、9月1日と10月1日の曜日差は右に2日、10月1日と11月1日の曜日差は右に3日、11月1日と12月1日の曜日差は右に2日になっている。
この曜日差については1583年でも9999年でも変わらねえ。
ただ、実際に計算をする時はこの月間曜日差を使うよりも、基準月と対象月の曜日差を直接使った方が速いだろう。
例えば6月1日を基準日とした場合、1月1日との曜日差は右に2日または右に3日、2月1日との曜日差は右に5日または右に6日、3月1日との曜日差は右に6日、4月1日との曜日差は右に2日、5月1日との曜日差は右に4日、6月1日との曜日差は0日、7月1日との曜日差は右に2日、8月1日との曜日差は右に5日、9月1日との曜日差は右に1日、10月1日との曜日差は右に3日、11月1日との曜日差は右に6日、12月1日との曜日差は右に1日、になる。
これを表にするとだいたいこんな感じだ。([ ]はガウスの記号)
a3a = ([(mm + 2)* 30.6 + 0.5] mod 7 + 3) mod 7 (平年3月以降)
a3b = [(mm + 14)* 30.6 + 0.5] mod 7 + 2 (平年1月2月)
a3c = [(mm + 14)* 30.6 + 0.5] mod 7 + 1 (うるう年1月2月)

ちなみにここの数式がぐだんぐだんになってるのはa3の値が惑星運動の周期とかとは完全に無関係で、グレゴリオ暦の適当な規定に従って実際に作成されたカレンダーから逆算しただけの値に過ぎねえからだ。
グレゴリオ暦のヤツがいかに適当な仕事をしているかのあらわれだな。
もし「30.6」って数字に見覚えがあるんだとしたら、それが横軸に経過月数、縦軸に経過日数を取って、どちらもが正しく成り立つ場所に点を取ったとき縦方向に伸びる1ヶ月分の線分の、すべての線上を通過するコトになる直線の傾きでしかねえコトくれえは理解できるな?
この「30.6」って値はすべての線上を通る値だったら何でもいいし、経過日数から月数を逆算する時なんかに30.6を使うとピッタリ過ぎてうまくいかねえから、オレなんかは30.61を使ったりするコトもある。
とりあえずうるう日が2月29日だから、それぞれの月初日が「3月1日から見て何日経過した日か」の具体的な数値も書いておくが、7日が過ぎる度に月曜日が来るんだから、この値を使えば月初日の曜日は確定できる。

だから計算できるかできねえかで言ったら確かに計算できるんだが、この部分を数式で解く意味は本質的にねえ。
現代文明レベルだと知識層の中に点在する老害連中がswitch-caseを数式としては認めねえだろうからあえてこんな形にしているが、それが数式として認められる時代だったらオレだってこんなバカみてえな数式は使わねえ。
まあa3については本来うるう日を完全に外にはじいて「a3 = ~~ - i」の形にまとめるべきだし、実際に過去のオレはそうしていたはずなんだが、その時のオレがどんな風に計算をしてたのかもすでに忘却の彼方だ。
もしかしたらifを使ってたのかもしれねえが、だとしたらどのみち今はそれが数式として認められる時代じゃねえし、そもそもここを数式化するのがバカの極みだ、っていうオレの意見に変わりはねえ。
a3についてはそんな数式なワケだから、ココの値については素直に丸暗記しておいたほうがいいだろう。
一度くれえは実際にグラフを描いてみるのもいいかもしれねえけどな。
実際に観察された現象から数式を組み立てる際にはこんなやり方もあるってコトについては経験しておいても損はねえのかもしれねえ。
グレゴリオ暦の改暦についてはとにもかくにも10日のズレは補正したワケだし、当時の時代背景を考えればそれでも大分革新的なコトではあったんだろうが、月々のアライメントをそのまま引き継いじまった、ってトコだけはどうにもいただけねえな。
どう考えても致命的な欠陥だ。
あとa3表の基準月は必ずしも5月である必要はねえから、たとえばテメエの誕生日なんかがある月でもいいし、ツェラーの公式なんかになじみがあるなら3月とかにしてみるのでもいいと思うぞ?
例えば3月1日を基準日とした場合、1月1日との曜日差は右に3日または右に4日、2月1日との曜日差は右に6日または0日、3月1日との曜日差は0日、4月1日との曜日差は右に3日、5月1日との曜日差は右に5日、6月1日との曜日差は右に1日、7月1日との曜日差は右に3日、8月1日との曜日差は右に6日、9月1日との曜日差は右に2日、10月1日との曜日差は右に4日、11月1日との曜日差は右に0日、12月1日との曜日差は右に2日、になる。([ ]はガウスの記号)
a3a - 2 = ([(mm + 2)* 30.6 + 0.5] mod 7 + 1) mod 7 (平年3月以降)
a3b - 2 = [(mm + 14)* 30.6 + 0.5] mod 7 + 0 (平年1月2月)
a3c - 2 = [(mm + 14)* 30.6 + 0.5] mod 7 - 1 (うるう年1月2月)

結局は切片の値が変わるだけなんだけどな。
だが、この3月基準の値を使う場合はa2表の値も逆方向に動くことになるからそこだけは気をつけろ。
一応はそれも表にしておいてやろう。
a2 + 2= ((yy + [yy / 4]) mod 7 + 2) mod 7([ ]はガウスの記号)

さっきちょっと話に出した、この世界のクソゲーの中でも最もクソゲーと評されるであろう
ってゲームの最初で選択できるAdjusterってヤツは、この部分の数値を調整している。
カレンダー計算については年内計算から始めるヤツがほとんどだろうからa2じゃなくてa3が基準になっているが、テメエがどんな数式を使っていて何年何月を基準にしていようが、Adjusterさえきちんと調整できれば必ずうまくいく組み合わせが見つかるハズだ。
もっとも曜日についてはISO基準で月曜が1になってるから、a4に切片値が出るようなタイプの数式を使ってる場合、たとえば自分の誕生日なんかを基準日にしてa4の値をずらしてるようなヤツらだと、ダイヤの列を逆算していく必要がある。
まあそういった連中はダイヤのカードを使わずにそのままたたかったらそれですむ話ではあるんだがな。
実際のところ、すでに自分なりの計算式を持っているヤツらはあのゲームの補助カードについては深く追求しねえで直接解答でたたかった方がいい。
別に追求したって構わねえが、ドツボにハマっても知らねえぞ?
すでに自分のスタイルを持ってるヤツが他人のスタイルを取り入れてみる、ってコトは、自分の脳内に流れる川の流れを組みかえてみる、ってコトでもある。
もしもテメエがトランプ1デッキまるまる覚えられるようなヤツだったら、新しいデッキを覚えても前の記憶に引っぱられて思わず間違えそうになる、って感覚については何となくでも理解できるだろう。
あれと同じで「これじゃねえ」ってことは分かるんだが、とにもかくにも複数の記憶(値)が呼ばれちまう、みてえな状況になることがある。
必ずしもそうなるとは限らねえんだが、補助カードの利用についてはちょっと試して合わねえと感じるようならやめておいたほうが無難だ。
一度変な癖がついちまうと元に戻るまでに結構な時間がかかる。
ところでa4の数式と表については何か説明いるか?
a4 = dd mod 7

もう見たまんまただのカレンダーなんだがな。
テメエこれ見てどうやって曜日計算するんだよ、って話になったら普通に「見ればわかる」ってなるよな?
実際のところ年内計算ができる驚異的計算者のほとんどは、a4表については何だかんだそのまま覚えちまってる場合が多いだろう。
そして曜日については
weekDay = (a1 + a2 + a3 + a4) mod 7
になるワケだから、a4表を覚えている場合、カレンダー計算は結局ただのスゴロクにしかならねえ。
たとえばa4表の形は2020年とか2026年の6月と同じ形になるんだが、6月と8月の曜日差は5日分だったな?
だから2026年8月18日は何曜日だ?ってコトになると、18 + 5 = 23 = 火曜日って感じで答えを出してもいいんだが、18日の木曜日から5つ数えて金、土、日、月、火曜日、って感じで答えを出してもいい、ってことになる。
百年計算にしてみたところで、a2の値が+2だったら水、木とさらに2マス進めばいいだけだし、万年計算の場合もa1の値が+3だったら金、土、日とさらに3マス進めばいいだけだ。
ところで16進数でccって言われた時、それが10進数の204だってすぐに分かるヤツはそれほど多くもねえんだろうが、256マスの正方形があった時にC列のC行目を指さすくれえなら誰にでもできるよな?
それと同じでカレンダー計算も実際には「値」の「位置」が分かりさえすればそれでいい。
「計算」をするんじゃなくて、「答えを出して」その値を「読み取る」。
だから速いんだよ。
オレ自身はソロバンとかやったコトねえからよく分からねえんだが、ある意味ソレに近いのかもしれねえ。
もしもカレンダー計算で驚異的計算者の速度にまで達したいんだったら、最低限a4の値は表として覚えておくといいだろう。
この表を49まで延長すればmod7なんて計算式も必要がなくなる。
まあ実際には5、6、6、31で48までしか出てこねえんだけどな。
以上でカレンダー計算の数式解説については終わりとなるが、ちゃんと理解できたか?
カレンダー計算の修得方法
さて、具体的なカレンダー計算の修得方法は大きく分けて2つある。
1つはカレンダーの仕組みや数式を理解しながら実際に計算を繰り返していく方法、もう1つは繰り返しカレンダーを見ながら見たものと記憶を結び付けていく方法だ。
たとえば2^8は?
256だな?
2、4、8、16、32、64、128、256……と倍々の道順をたどりながら覚えていったヤツもいれば雑誌やインターネットで繰り返し256って数字を見ているうちに自然と2^8が結びついちまった、ってヤツもいるだろう。
カレンダー計算もそれと同じで、どっちの方法を選ぼうと結局は「見れば分かる」の境地にたどりつく。
実際のところオレの場合、年内計算は見て覚える方式、万年計算は実計算方式で修得しているが、値の呼び出し速度に大差はない。
どんな方法で覚えたかよりはむしろ「何回計算したか?」、「何回思い出そうとしたか?」、つまりは試行回数の方が重要になってくる。
水が流れ続けて川になるとき、その水が雨水か湧き水かはあまり関係がねえのと同じだ。
見たものと記憶を結び付ける方法の場合、年内計算であれば日付と曜日の関係性が「見れば分かる」ようになるまでに必要な「見る回数」は個人差もあるだろうがおそらく数千回程度だろう。
当然ただ見るだけじゃなく、それと同じ回数の「思い出す」をくり返すことができなければ「見れば分かる」ようにはならねえけどな。
見たものと記憶を結び付ける感覚がよくわからねえ、ってヤツは自室の隅っこにでも適当にトランプを並べておくといい。
それで部屋を出るたびそのトランプの並びを思い出してみろ。
そのトランプの並びはテメエが変えない限りは絶対に変わらねえ。
「邪魔くせえなこのトランプ」とか思いながらも片づけねえでいると、最初は4、5枚しか覚えていなかったはずのそのトランプの並びも、1か月しねえですべて覚えちまうハズだ。
そしてカレンダーの日付ってのは、そのトランプの並び以上に変わらねえんだよ。
毎日見てたら普通に覚える。
そして「xx月xx日は何曜日?」って聞かれたときにその構造を思い出す。
何度かそれを繰り返すと次にきかれるときに備えて自分でその質問を繰り返すようになる。
すると思い出す速度も自然と速くなる。
特にガキの場合は、テメエらが思っている以上のペースで速くなる。
しかも記憶は変遷する。
過去のオレはカレンダー12枚を間違いなく覚えていたし思い出していたが、いつしか思い出す枚数は7枚に、そして1枚になり、
最後には1枚も思い出さなくなった。
思い出す必要がなくなったからだ。
そんなものは思い出さねえでも完全に構造が把握できる。
自分の腕は何本あるのか?
それぞれの腕には手がいくつあって、それぞれ何本の指があるのか?
それぞれの指の位置関係は?
テメエらだって、そんなの思い出すまでもなく自然と把握してるよな?
それどころか、むしろ自在に動かせる。
カレンダー計算に必要な「値」も、最終的にはそれと同じくらい自然な記憶になってくる。
そしてこの頃には根本的な記憶の呼び出し方そのものが変わる。
脳も筋肉の一部と考えて動かそうとすると、そこに格納されてる記憶が返ってくる、みてえな感じだな。
カレンダー計算において扱う対象は主として数字だが、当然のことながら数字も結局は文字であり記号だ。
そして記号(文字)は言語(音信号)よりも新しく、言語は運動よりも新しい。
文字を言語化してさらに運動化するのが音読(口述)であり、文字を直接運動化するのが書写だ。
つまり外部から入力された情報に対してなにがしかの答えを外界に「返す」場合、その処理はほぼ確実に小脳を経由するし、そもそも小脳系は人体すべての受容器から求心性経路を受けている。
ココの記憶をうまく使ったらいい。
テメエらだってウメボシ族を見たらヨダレくれえ出すだろ?
実際に食う食わねえは関係ねえし、蜂蜜漬けの高級品だから実は甘い、なんて事実も関係ねえ。
この時テメエがヨダレ出してんのが「いわゆる」ワーキングメモリの作用じゃねえコトは分かるな?
ウメボシ族の「見た目」と「味」は、それぞれ別の感覚だ。
当然、記憶の場所も違う。
だが、テメエの小脳はソレらの情報を「同時」にまとめて受け取った過去がある。
それがトラウマになって「この見た目はヤベエ」ってコトになってんだよ。
コレはある種の共感覚に近い。
おそらく脳内の各器官もそこまで厳密な時間の概念は共有してねえんだろうが、物理的時間の「同時」と心理的時間の「同時」は完全に別モノだ。
たとえばテメエがウメボシ族をスッパイと感じる時、すでにウメボシ族はてめえの口の中にあって視界にはねえ。
だが、小脳内で異なる2つ以上の情報を結び付けまとめて扱う時、信号到達の物理的タイミングがどうであれ、テメエの脳内じゃそのタイミングは必ず「同時」として扱われれる。
逆に言えば、「同時」に扱われた情報は必ず結び付けて記憶されるし、結びつけられた情報は必ず「同時」に思い浮かべるコトができる。
「お前の脳はお前が過去に『見て』『呼んだ』値を覚えている」
つまりウメボシ族を見た時に「スッパイ」と感じるのと同じ要領で自分が見た日付と自分が呼ぼうとしている値を結び付けることができれば、値の呼び出しは瞬時におこなわれるようになる。
もちろん日付を見て「スッパイ」「甘い」なんて感覚を呼ぶ必要はねえぞ?
普通に「紫の12」→「4」みてえな感じで呼べばいい。
これができる状態になると曜日の計算に必要な「値」の呼び出しはワーキングメモリの外で行われるようになる。
ワーキングメモリ使って2、4、8、16、32……なんてやらねえでも「256」が直接ワーキングメモリに入ってくるんだから、その値を使って足し算でも引き算でも好きにやればいい。
端的に言ってオレがカレンダー計算をする時、オレのワーキングメモリにかかっている負荷はお前たちが考えているよりもはるかに低い。
しかも実際にやってるのは足し算じゃなくて、数式解説の最後でちらっと説明したスゴロクみてえなもんだ。
もちろんスゴロクする時も、具体的なスゴロク板の画像や映像みてえなものをいちいち思い浮かべる必要はまったくねえぞ?
オレの脳内にはこの49マスそれぞれに対応する活性化した細胞群がある。
これをそのままスゴロク板にしたらいい。
もちろんこのスゴロク板は平面じゃなくて立体だ。
手のひらと同じでな。
その意味じゃマスと言うよりはブロックに近い。
しかもこの活性化した49の細胞群の間にはさらに無数の活性化した細胞群があるから、オレの扱う信号はこの細胞群の間を横移動だけでなく縦移動もできる。
むしろ斜めにも移動する。
さらに言うならそもそも移動する必要がねえ。
ワーキングメモリ内での値の呼び出しを2^8 → 2 → 4 → 8 → 16 → 32 → 64→ 128 → 256みてえな感じの 1ブロックごとの移動とすると、ワーキングメモリ外からの値の呼び出しは2^8 → 256みてえな感じのワープに近い。
もう少し具体的に言うと、「おい」って言ったら「ヘイ!」って感じで答えが返ってくる感覚に近い。
移動するまでもなくa1、a2、a3、a4の4つの回路から、4つの「ヘイ!」が返ってくる。
その4つの「ヘイ!」が、結局は1つの答えを示している。
お前らだって音符で「ソドミソ」ってかいてあったら「あの音か」ってなるよな?
ある意味でその感覚に近い。
4つの「ヘイ!」は「土曜日」とイコールじゃねえんだが、4つの「ヘイ!」を重ねた結果が土曜日を意味することはわかる。
4つの「ヘイ!」、ソドミソの表記が直接オレのたどりつくべきブロックを示している。
だが、このとき返ってこない「ヘイ!」があると、結局オレは間違ったブロックにたどりつくことになる。
まあ自分が間違ったブロックにいることと、a1、a2、a3、a4のどの「ヘイ!」が足りてねえのかとはわかるんだから、足りねえ値をワーキングメモリから呼んでやればいいだけなんだけどな。
このとき呼んだ値は「音」として呼ばれる。
だから1つも「ヘイ!」がかえってこねえと、「今日の5晩メ3シ6何に1すっかな?」みてえなコトが起きる。
もちろんカクテルパーティー効果みてえな感じでちゃんと区別がつく。
実際の「音」でなく脳内情報であれば両方の内容を同時に把握するコトも普通にできる。
「ヘイ!」(音符)と「値」(音)が混ざった場合は、必ず「値」(音)での計算が必要になる。
その意味じゃ音での暗算も鍛えておく必要はある。
音として呼ばれた値を「ヘイ!」(音符)になおすのは逆に時間がかかるからな。
味噌ラーメンから味噌だけ取り出して味噌汁につくりなおす、みてえな感じだ。
せっかくできた味噌ラーメンから味噌だけ取り出す意味も分からねえし、普通にそのまま食っちまったほうが速い。
味噌の分量さえ分かればそれで問題ねえ。
もっとも、この「音」にしたって必ずしも完全な味噌ラーメンの形で呼ばれるとは限らねえ。
たとえば「3」の値が音韻側に呼ばれる場合、「サン」まで呼ばれるまでもなく「サ」のあたりで終わる時もあるし、「サ」にすらならねえ出だしの部分の何かで終わる時もある。
それでも内容は理解できる。
完成した味噌ラーメンを見なくても材料を見たら何をつくろうとしてるのかはわかるし、材料を見るまでもなくレシピを見たら何をつくろうとしているのかはわかる。
何千回何万回と同じ値を繰り返し呼び出していれば、結局はそうなる。
だから結果的には音符の一部が音がになっちまったとしても、答えをだすのがそこまで遅くなってる、ってわけでもねえ。
日付を見た瞬間に一発で「ヘイ!」が呼べねえと「音」になる。
a1だけが音になったなら残りの「ヘイ!」を重ねた結果スゴロクでたどりついたブロックの値を音になおしてa1と足す。
要するに音としての暗算になる。
音としての暗算とスゴロクなら、基本的にはスゴロクのほうが速い。
だがそれは必ずしも最短経路とはならない。
その時々の脳のコンディションによって、最適な細胞群がそれぞれに答えを返してくるからだ。
よりごのみをすればむしろ計算は遅くなる。
何にしても、同じ信号は繰り返し呼べば呼ぶほどより小さくより短く、それでいてより強くより正確になっていく。
発火する細胞が増え、その結果が収束していく。
密度のあがったより強い信号がうまれる。
この信号を練り上げていくことこそが、カレンダー計算修得の基本だ。
最後に
これを読んでカレンダー計算に挑戦するヤツがどれくらいいるのかは知らねえが、挑戦して成功するヤツもいれば失敗するヤツもいるだろう。
これは別にカレンダー計算に限ったコトでもねえんだろうが、だいたいのヤツらは10回とか20回とかの失敗で純粋さを失う。
そうじゃねえヤツらも100回とか200回とかの失敗で純粋さを失う。
どこまでもどこまでも純粋さを保って限りねえ挑戦を続けていくためには、何の嘘も偽りもない真っ白な心が必要になる。
「お前たちには純粋さが足りない」
だからカレンダー計算ができない。
カレンダー計算を極めるために必要なのは心の平安、温和、沈黙、自己の抑制、心の清浄だ。
接待、尊敬、崇拝を得るために行われる計算は動揺し不確実になる。
帰結、損失、能力を無視して迷える見解に固執し、自己を苦しめ他者を打ち負かすために行われる計算は破滅への門と理解しろ。
カレンダー計算なんかできるようになったところで、世間の扱いは「すごい!」じゃなくて「アホか?」だぞ?
「オレのほうが速い!」とか言ったって結局はケンカになるだけだ。
やるならやるで、最初にそれを理解しておくといい。
目の前の重荷を持ち上げる時、結果に結びつく筋繊維もあれば無為にちぎれるだけの筋繊維もある。
それでも結果は目的にむかって収束する。
その時自分に何が起きているのか、そして世界に何が起きているのか、それを理解できる筋繊維は少ねえ。
人族にしたって同じだ。
もしもテメエが何かの役割を持った一本の筋繊維のような存在で、何度千切れてもたまたま修復されて、この先もずっとカレンダー計算を続けていつの日か驚異的計算者の域にまで達することができたとしても、そのときテメエに理解できる事はただ一つ、
「自分は今もカレンダー計算をしている」
くれえのことでしかねえはずだ。
だが、それと同時にそのことだけはこの世界の誰一人として決して否定することのできねえ、厳然たる真実の「一部」になっているだろう。
テメエに真実の全貌を把握することができねえとしても、真実の形は変わらねえ。
約束の地にたどり着くことができるヤツもいれば、それができねえヤツもいる。
それでも真実の形は変わらねえ。
驚異的計算の本質はワーキングメモリ「内」における足し算引き算や数値移動の速さよりも、ワーキングメモリ「外」からのデータ呼び出しとその呼び出しの速さのほうにある。
大切なのは必要な情報の伝達で、その伝達は速ければ速いほどいい。
そのための回路を構築し信号を最適化すること、それこそがカレンダー計算の極意だよ。
テメエが真智の目的を考察して人生の勝者となる事を祈るぜ。
(完)
いいなと思ったら応援しよう!

