ノーベル物理学賞(2024年)をクールに語ろう! その7
その6をアップしてからかなり間が空いてしまいました。機械学習そして深層学習の理屈をあれこれ学んで頭に消化するのに少々手間取りました。
幸いなんとか呑みこめた、と思います。その成果が出ているかどうかは、皆様が判断してください少なからずプラスに出てくるだろうと私自身は夢想しております。
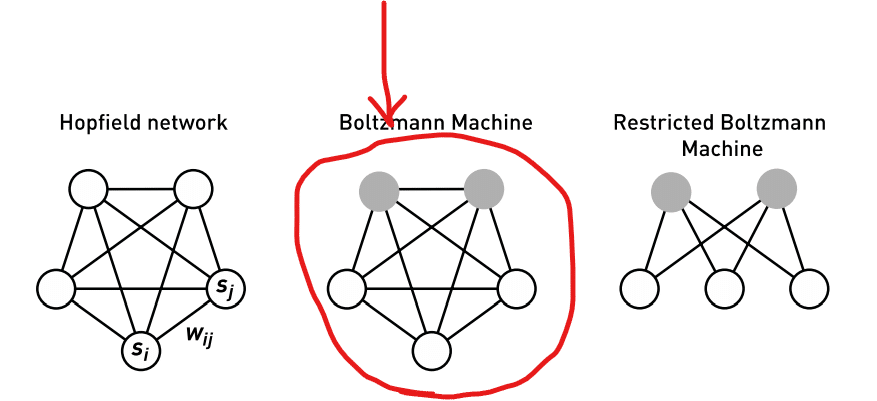
どこまで話したのだったかな… ①ホップフィールド・ネットワーク、②ボルツマンマシン、③制限ボルツマンマシン、この三つのうち②までを語りました。(下図の、左から順に①、②、③)
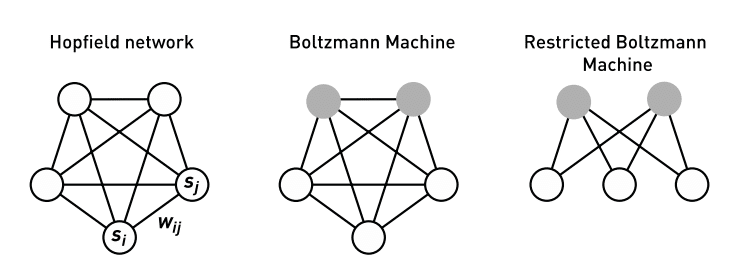
右端の図つまり ③制限ボルツマンマシン について今回より語っていくつもりだったのですが、その前に①と②について、これまでの解説よりもっと直観的にわかるような解説をしてみたくなったので、これよりやってみます。
直観的? そうです。前にこんな話をしました。あのホーキング先生があの書物を書き下ろされるにあたって「方程式をひとつ挿し込むたびに、潜在読者数は半分になっていくよ」と耳打ちされたのを受けて、彼は腹を括って、使う方程式はただ一つ $${E=mc^2}$$ にしたという、あの逸話。
さらには本文中でこの方程式を、彼は三回しか挿しこまなかったのです。
その心意気というか開き直りというか、その根性を見習ってですね、私も数式をひとつしか使わないで、①ホップフィールド・ネットワーク と、②ボルツマンマシン について語ってしまおうと、そう考えるわけですよ。
これがホップフィールド・モデルである
式を使わず、これを使う。

うまく正五角形を描けなかったのが悔しいですWORDでちゃちゃっと作った代物ゆえ、どうかご容赦ください。ホップフィールド先生が編み出されたのは、この多角形です。上の絵では五角形ですが三角形でも十一角形でも一億二千十七万四千九百八十七角形でも、とにかく何角形でもいいです。
この多角形には〇があります。野球でいうとベースですね。一塁ベース、二塁ベースなど。
五角形の場合、各ベースにひとがいるかいないか、その組み合わせはいくつでしょう? 簡単な計算でわかります。
答えは $${2^5}$$ です。32通りです。
すべての組み合わせを列挙するのはめんどうなので、以下そこそこ並べてみると…
(0, 1, 1, 0, 1)
(1, 1, 0, 1, 0)
…
(1, 0, 0, 1, 1)
ベースの上にひとがいたら「1」、いなかったら「0」と解してくださればいいです。たとえば最初の数列(0,1,1,0,1)はこんな風。

ちなみに上段左のベースから右回りと設定してありますが、お望みならば左回りでもいいしほかのベースからスタートでもよろしい。私の気まぐれで上のようにナンバーを振っていくことにします。(以後これで統一)
各ベースへの「0」と「1」の割り振り方が、五角形の場合は $${2^5}$$ 通りというわけです。

ホップフィールド・オブ・ドリームス
ここからが本題です。ホップフィールド先生は、この五角形に面白い仕掛けをしました。


「はあ?」と⇧を見て思った方もいらっしゃると思いますがここに彼の天才があります。
各ベースをこうやって必ず線で結んでですね、このネットワークをうまく管理するとですね…
面白いことが起きるのですよ。
並び替え・その1
例えばこんな風に数字を振るとしますね。

次に、このネットワークに電気を流します。すると…

おっと、数字が少し変わりました。
さらに電気を流すと、今度は…

「変わんないじゃん」と思ったあなたは正しい。そうです変わらないです。電気を流すたびに並びが変わるのだけど、何度かそれを繰り返すと、以後変わらなくなる、そういうネットワークさんなのです。
並び替え・その2
もうひとつやってみましょうか、こんな風に。
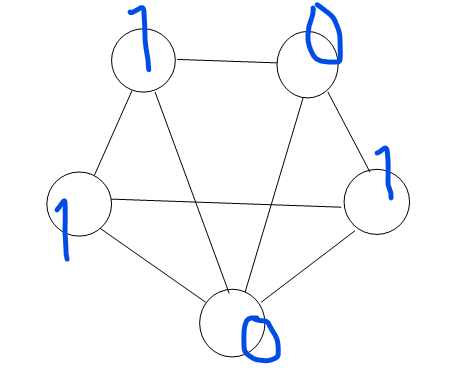
電気を流すと…

並びが変わらない。そこにまた電気を流すと…

「変わんないじゃん」と思ったあなたは正しい。電気を何度流しても変わらない組み合わせが存在するのですよ。
並び替え・その3
もうひとつやってみませう。

電気をこのネットワークに流すと…

いくつか変化しました。そこに再度、電気を流してみると…

さらにいくつか変化しました。ここにさらに電気を流してみると…

今度は変化なしですね。つまりこれ以上電気を流しても、数字の並び替えはおきないのです。
並び替え・その1~3を総括すると
以上、三つのパターンを見てみたわけですが、何か気づきませんでしたか?
三つとも、最後はこの組み合わせに落ち着くのですよっ!
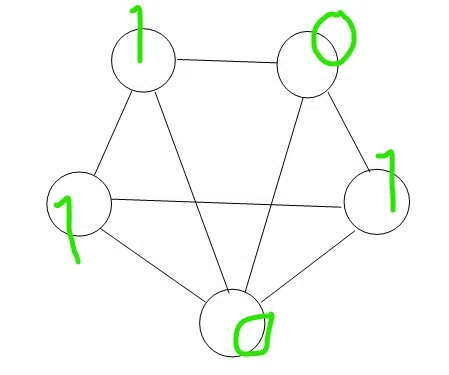
「おーっ!」と感動してもらえるとうれしいのですが… この五角形ベースに、どんな組み合わせをしても、電気を流すたびに組み合わせが変わって、最後はどれも同じパターンに落ち着くのです。
すごいでしょすごいでしょ、これが今年(2024年)ノーベル物理学賞授与となったジョン・ホップフィールド教授の捻りだしたネットワークです。
ふたを開けると裏側に…
いったいどういう仕掛けでこうなっているかというとですね、本当は数式をお見せするのが筋なのですが(実際過去の回でお見せしていますし)今回はわたくしホーキング教授に倣って数式はひとつしか使わないつもりですので、こんなのをお見せします。
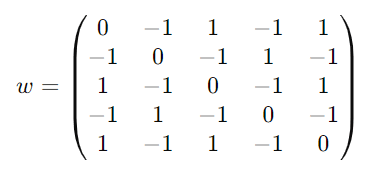
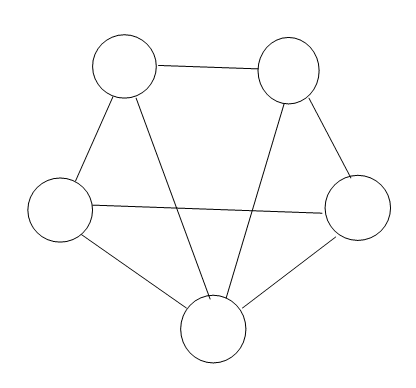
「なにこれ5×5行列?」と思ったあなたは賢い。行列です。この行列は、五角形のベースを結ぶ、各線分を表しています。
この写真は、むかあしの電話交換手です。電話をかけるとき、こうやって人力で電話回線をつないでいたのです。

それと似ていますこの行列。違うのは、この行列さんにお願いすると、何度か試行錯誤をした末に、最後は同じ電話番号につないでしまうところです。
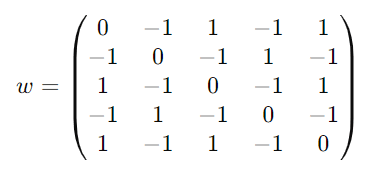
変な電話交換手さんですね。しかし考えようによっては、こういう電線の組み合わせで「記憶」を保っているともいえるわけです。
ドクター・脳
脳の神経細胞には記憶の機能があります。しかしどういう配線によって記憶が保たれているのかは、ずっと謎のままでした。
しかしこのモデルを使うと、人工的に脳神経の記憶機能を、再現できてしまうのです。
おもちゃに毛の生えたような仕掛けですが、これが画期的でした。こんな素朴な仕掛けで、脳の働きを人工的に再現できる(かもしれない)ということで、ホップフィールド教授は賞賛されました。
実はその十年ほど前に、日本の研究者が同じ仕掛けを提唱していてしっかり論文で世に問うていました。ホップフィールド先生がノーベル賞というのならば、甘利というこの日本人研究者さんも共同受賞でないとおかしいという声が、日本ではくすぶっています。
どうして彼は選考で落とされてしまったのか?その謎解きは後に行うとして、このホップフィールド・ネットワークがどういうものかについては、皆さんには感じをつかんでいただけたかと思います。
次回、②ボルツマンマシン について同じノリで語っていくよっ!