
ノーベル物理学賞(2024年)をクールに語ろう! その6
その5はどこまで語ったのかな…続きを語っていく前におさらいしましょそうしましょ。
.
*
.
その2で仕分けのメカニズムについてちゃちゃっと語りました。こういう重み行列を事前に用意して…

そこに二進法で、たとえば [1 1 1] という情報を放り込んで、何度か繰り返し演算させると、最後には [1 -1 1] に収束します。
この行列Wのなかには [1 -1 1] と [ -1 1 -1 ] の二つが記憶されています。
そしてこのWにいろんな組み合わせ、例えば [1 1 -1] とか [ -1 -1 -1 ] とか、いろんな組み合わせを放り込んで繰り返し演算させると、最終的には必ず [1 -1 1] と [ -1 1 -1 ] のどちらかに仕分けされるのです。
この摩訶不思議なメカニズムを回しているのが、この数式です ⇩
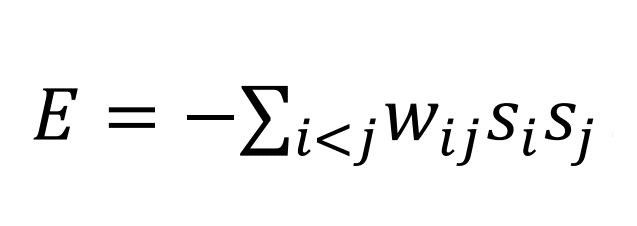
この数式が、こういうネットワークに仕込まれると…

私がいうところの「仕分け」が自動的に回りだします。
手書きの郵便番号を、機械が自動的に0から9までのアラビア数字のどれかに仕分けしてくれる、ああいう感じです。

自動仕分けにはいろんなメカニズムがあって、そのなかで一番素朴かつもっともすっきりしているのが、再度お見せしますがこの数式です ⇩
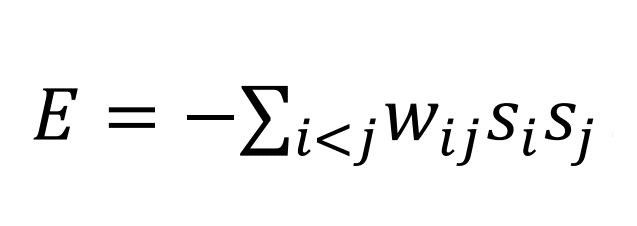
*
以上おさらいおわり、今回の本題に進みます。
上の式に、新たにこんなのが加わった数式について、です。

この紫で括った部分は、自働的に学習するメカニズムを表しています。
先ほどお見せした区分けマシンは、人間さまが事前に行列Wを用意してあげないといけなかったわけですが…
これを新たに付けると、行列Wを、マシンが自動的に調整してくれるのです。

…というのは半分うそで、調整用の数式(=ごく素朴な微分方程式と思ってもらっていいです)がほかにあって、それと⇧を連動させると W の値がだんだんと調整されていきます。
実際の演算工程を見せろ、ですか… ちゃちゃっと要点に絞って説明します。
ニューロンネットワークのニューロン数を、三つに設定します。(少ない方が一目でわかるから)

ここにある三つの〇(ニューロン)が、それぞれネットワーク化されています。直線が三つの三角形になっていて、それぞれの線の「重み」は、どれも同じと初期設定してあります。
それから各〇(ニューロン)が、それぞれ1か0を表すとして、その組み合わせ方は最大で8通りですが、わかりやすさ優先でここでは以下の3通りとします。
例えば、こんな風に三つの組み合わせが、ランダムに百回出るとしますね。
(0, 1, 1)
(1, 0, 1)
(1, 0, 1)
(1, 1, 0)
…
100. (1, 0, 1)
頻度を計算すると…
(1, 0, 1) が40回
(0, 1, 1) が30回
(1, 1, 0) が30回
出現頻度に偏りがあるわけです。この偏りぶんを、くだんの式の以下の二つに反映させます。

次に、サンプルの1回目を、⇧に入力して $${E}$$ の値が一番小さくなる $${w_{ij}}$$ と $${θ_i}$$ 組み合わせを、探していきます。
(探すアルゴリズムがちゃんとあります。それはこの数式とは別に用意されています。「ボルツマン分布」と呼ばれる、古典物理の有名な数式を応用したものです。古典ですのでここでは説明を省きます)
「$${E}$$ ってなんやの~?」と思われた方は、数回前に貼った、この図を思い出してください。

水は高きから低きに流れるの法則、すなわち位置エネルギーが段々小さくなっていく方向に水は進んでいきます。
くだんの式でいうと、ここです。これが位置エネルギーにあたるものです。

この $${E}$$ が小さくなるように、パラメータを調整していきます。

そしてこれ以上 $${E}$$ が小さくならない組み合わせが判明したら、それを正解として、上に式において固定化します。
次にサンプルの二つ目についても、同じような作業を行って、これ以上 $${E}$$ が小さくならない組み合わせが判明したら、それを正解として、続いて三つ目のサンプル[中略]そして百回目で演算終了。
以上が機械学習のプロセスでございます。
行列Wを、人間がいちいち事前に計算しておくのではなく、百のサンプルを用意しておけばマシンが自動的にそれを元に行列Wを調整していって、やがてベストのものにたどり着く…のです。
本当はその演算工程を、易しい実例とともに順に見せていくことを考えていましたが、長くなるので今回はしないでおきます。
*
そうそうパラメーターの調整を行うにあたって、重宝するのが赤で括った式です。比例式。「ボルツマン分布」という偉大なるものです。
これがくだんの $${E}$$式の、パラメーター調整を取り仕切っております。


このボルツマン分布を使った機械学習マシンということで「ボルツマンマシン」と命名されました。(真ん中の図)

左側のがホップフィールド・ネットワークですね。そして右側にあるのは「制限ボルツマンマシン」と呼ばれるものです。
次回よりこのセーゲンぼるつまんましん(一番右の図)について解説していきます。
