
花道くんに物理数学を面白がらせる
数学や物理学の学習コツ集を、書き下ろしてみたいと前から夢想しています。
またその話?といわないで少しだけ私のつぶやきにおつきあいくださいな。
物理数学の本を読んでいると、違う分野の数式や方程式でありながら形式が実によく似ているものをいくつか見かけます。
試みに生成AIに「そういう実例を挙げてみてくれる?」と誘ってみたら…
.
波動方程式と熱伝導方程式
シュレディンガー方程式と拡散方程式
ポアソン方程式と重力場の方程式
マクスウェルの方程式と流体力学の方程式
.
うーんそんな高邁なものではないのですよ私がイメージしているのは。


見ての通り、コーシー・リーマンの関係式と正準方程式は、同じ形をしていますよね。
実はこの二つ、ストークスの定理と血縁です。濃~い関係にあります。

さらにはコーシーの積分定理それに積分方程式とも血縁があります。(以下がそれぞれそれです)
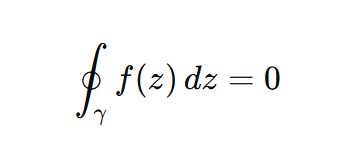

これらに共通するのは、座標平面上に視覚化すると、そこに回転が現れることです。
それからある一点に全体の姿(の情報)が集約されるところも。
ここから後半
これらの遺伝子情報的共通項は、突き詰めればオイラーの公式まで行けます。

要は左回りの回転を表したものだから、回転の遺伝子を有する上記のいろいろな数式と血縁ありといえそうです。
.

私、前に虚数について、こんな風に教えていくのはどうかという随筆を綴ったことがあります⇩
.
.
今の私が読むと、無限小の議論が緩いかなーというところですが、今読んでもいいこと言ってますね少し前の私。
「単位が取れればいいや」な大学生向けの体裁で、背伸びしたがるお年頃の高校生や早熟中学生や神童系小学生向けに、面白いコツ集を書き上げたいなって、ずっと夢見ています。

