ぼくが数学オリンピックに出ろってか、ワトソン君？

こんな問題です。

Ｊ君が九九の表に載っている数(1以上9以下の数2つの積として表される数) の中から5個を選んだところ、いずれも2桁であり、一の位または十の位に 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 がちょうど1度ずつ現れていることに気がついた。 Ｊ君が選んだ数のうち、一の位または十の位に5が現れるものを答えなさい。
ただし、2桁の数として十の位が0であるものは考えないものとする。

問題文の意を読み取るのでもはや大変なので、とっとと解き方をお見せします。以下の九九の表をご覧ください。

ここからですね、同じ値のものは消していって、それぞれひとつ残していきます。

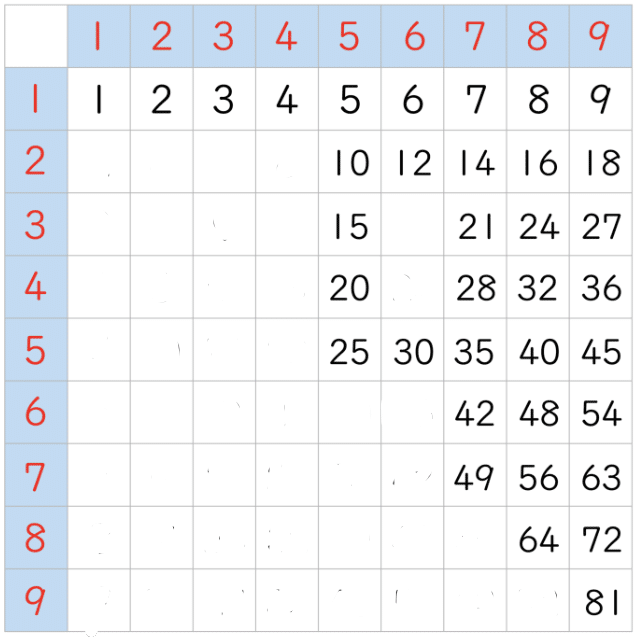
おおいきなりすっきりしてしまいました。せっかくなので、同じ数字の組み合わせのものも、順に消していって、それぞれひとつ残していきます。

たとえば「２４」と「４２」があったら、どちらかを消して、ひとつにするのです。

ああそうそう、一桁のものを消すのを忘れてた。

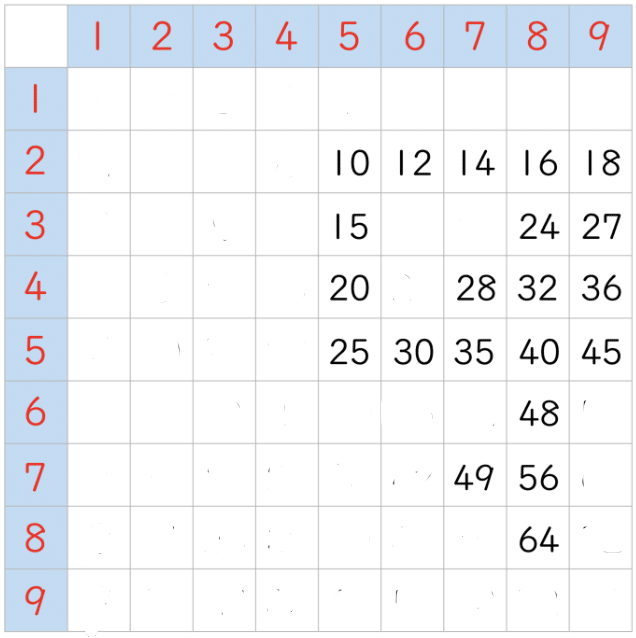
これで２１個のマス目が残りました。

ここで問題です。この２１個のなかから、五つ選んで…

０，１，２，３，４，５，６，７，８，９

以上の１０個の数字が、すべて揃うようにしてください。

＊

答えを先に言ってしまうと、「49」「27」「18」「30」「56」の五つを選べば…

４９，２７，１８，３０，５６

すなわち

０，１，２，３，４，５，６，７，８，９

が揃います。

どうやって「49」「27」「18」「30」「56」の五つを選び出すのかというと…

最初に「９」を探してみることです。

「49」マスにしか「９」が出てこないのは、目で追えばすぐ気づくと思います。

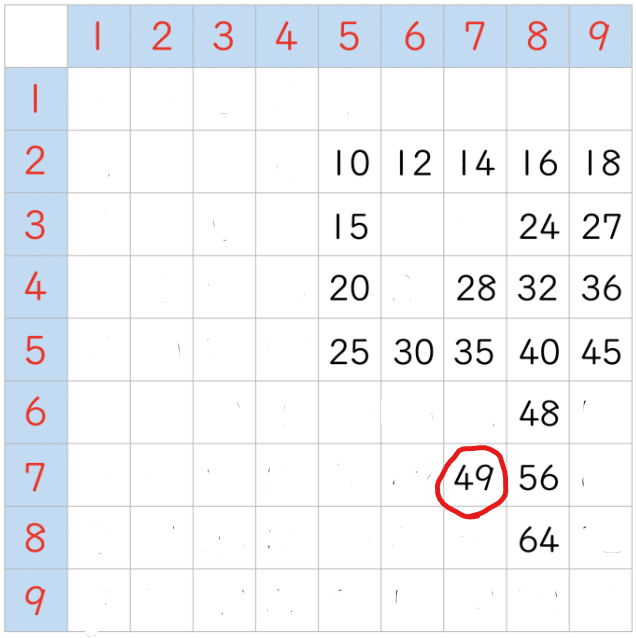
ということは「４」「９」については、この「49」でカバーできるので、ほかのマス目で「４」と「９」が含まれるものについては、自動的にお役御免となります。「９」は上の「49」にしかないけれど、「４」はほかにいくつかのマス目にも出てくるので…

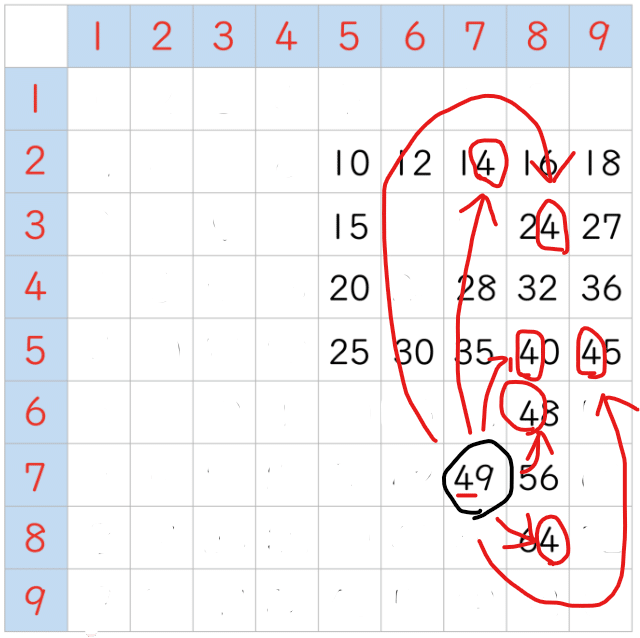
それらを消し去ると…

「９」と「４」がこれで一掃されました。次になすべきことは、上の表のなかで、一回しか出てこない数を探すことです。探してみてください。

これです。「27」マス目にある「７」です。「７」はここにしか出てきません。

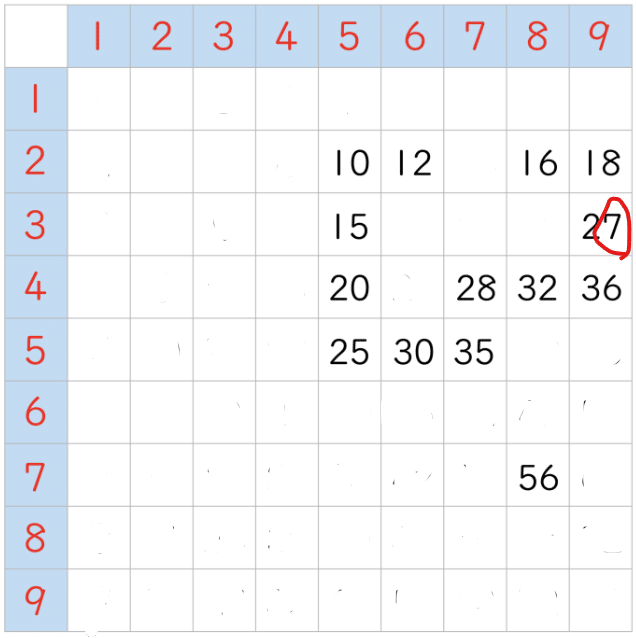
ということはこの「72」がこの「７」といっしょに、「２」もカバーするわけです。そういうわけで「７」と「２」があるマス目を特定して…

すべて消してみましょう。

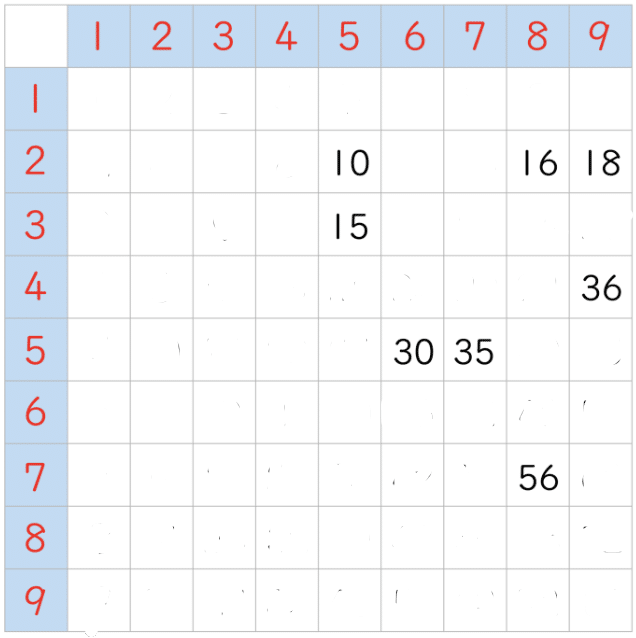
だんだんすっきりしてきました。ここでまた同じ作業に入ります。上の表で、一回しか出てこない数はなんでしょうね？

「８」ですね。

これで「18」のマス目が消せて、それに伴って「１」の含まれるマス目も消せます。

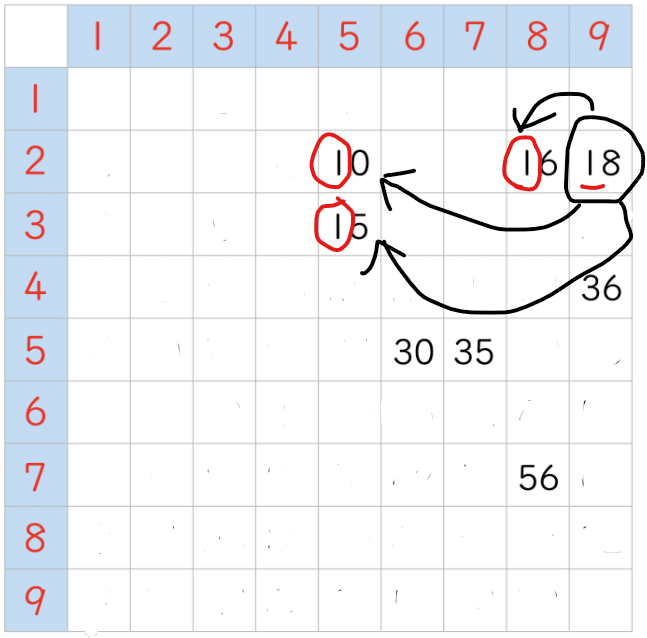
こんな風に。

そしてまた同じ作業です。一回しか出てこないのは「０」ですので…

「30」とともに「３」が消せて…

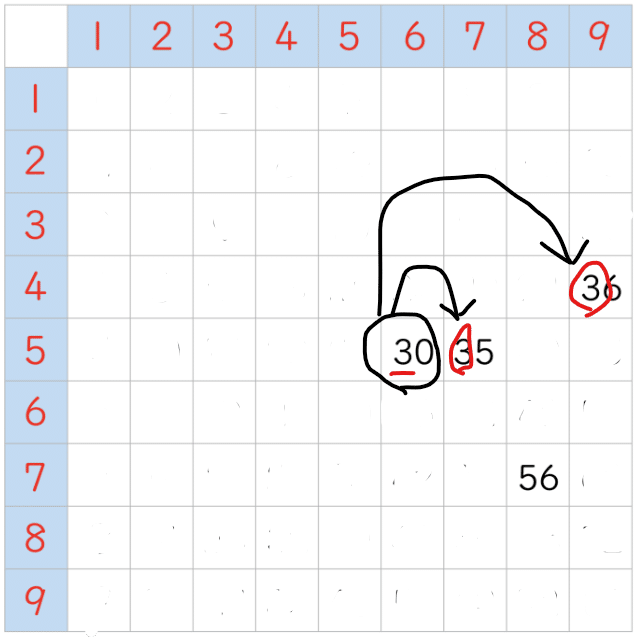
残るは…

「56」さんが残りました。

以上の絞り込みを順に振りかえると「49」と「27」と「18」と「30」と「56」の五つで、０から９までのすべての数がカバーできるということになります。

この問題、最初は整数問題と思いました。素因数分解して解くのかなーって。

しかしこうやって九九表を書き出して、こういう風に候補を絞り込んでいくと、機械的に答えが出るのですね。整数論ではなくて、代数ですこれ。ある一定のルールに従って回る、演算の体系。

これって何かに似ていると思ったら、シャーロック・ホームズの暗号解読ですわ。

アルファベットにそれぞれ対応した、変な人形（ひとがた）絵の連なりを、頻度から「これはたぶんＥ」「ということは、これはＴＨＥだろうからＴとＨに対応するのがこの人形だ」と、すべての人形にＡＢＣを当てはめて完全解読し、今度はそれを使って犯人をおびき出して捕まえるという、あのお話です。

この数学五輪予選問題は、数学の問題というよりは、九九表を暗号表に見立てて、ある素朴な暗号を解いてみろってことです。「５」はどんな数字といっしょに現れるかなワトソンくん？みたいな。

「・・・６だねホームズ」

見事だ、それでこそぼくの相棒だよ！

［追記］九九表でなくても同じ問題を作れます。詳しいことは後の機会に。